Презентация на тему: Средние величины

Средние величины Средняя величина обобщает качественно однородные значения признака.

Виды средних:

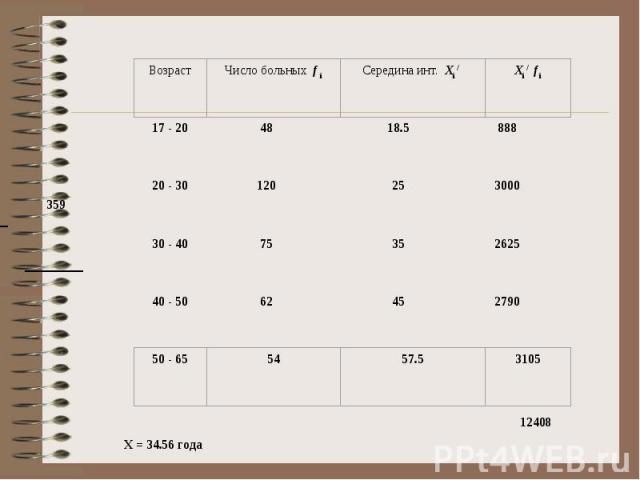
взвешенная средняя арифметическая

X = 34.56 года

средняя квадратическая

средняя квадратическая

средняя квадратическая

средняя квадратическая

средняя квадратическая

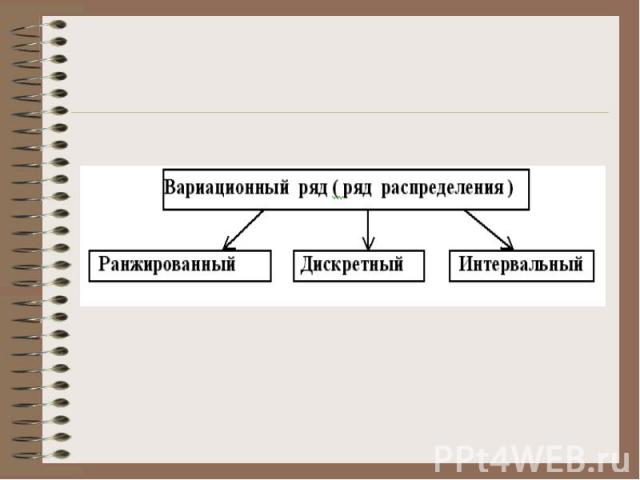
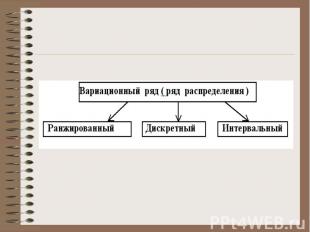
Вариации массовых явлений Вариацией значений какого - либо признака в совокупности называется различие его значений у разных единиц данной совокупности в один и тот же период или момент времени . Вариационный ряд - упорядоченное распределение единиц совокупности по возрастающим / убывающим значениям признака и подсчет числа единиц с тем или иным признаком.

средняя квадратическая
средняя квадратическая

Как определить число требуемых интервалов в интервальном вариационном ряду? Формула Стержеса : k = integer

тогда, ширина интервала:

Структурные характеристики вариационного ряда

Медиана распределения Медиана - это численное значение признака у той единицы изучаемой совокупности, которая находится в середине ранжированного ряда. Медиана делит совокупность на две равные части. Первая половина единиц статистической совокупности (после ранжирования!) имеет значение варьирующего признака меньше, чем медиана, элементы из второй половины совокупности - больше.

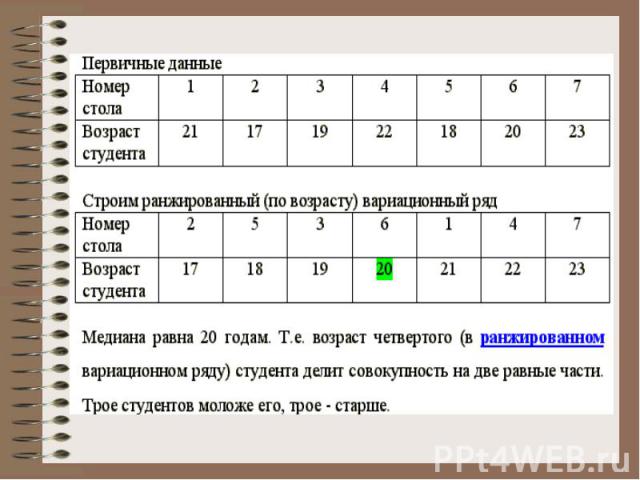
Пример: группа из 7 студентов в возрасте от 17 до 23 лет сидят в аудитории за семью столами. Вариационный признак - возраст студента.
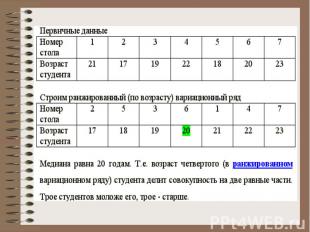

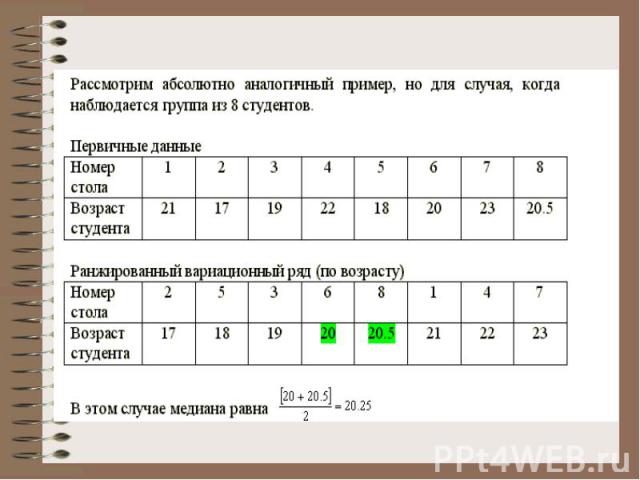
Если число единиц наблюдения (число элементов статистической совокупности) четное, то медианой считается средняя арифметическая из значений признака у двух серединных членов совокупности.
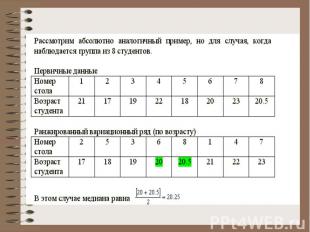

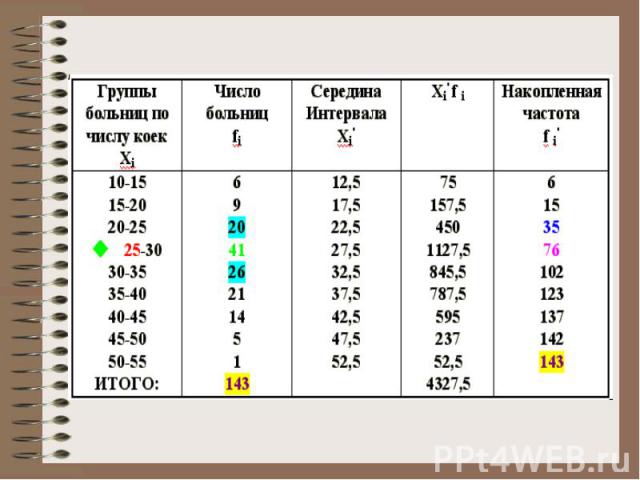
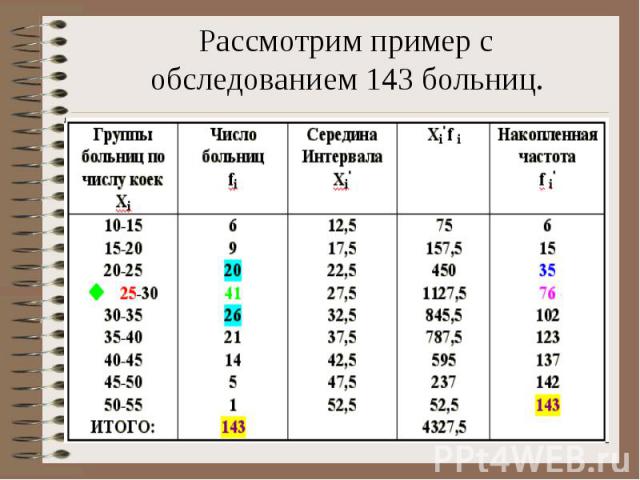
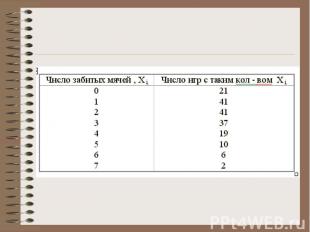
Определение медианы по интервальному ряду Предположим, что первичные данные обработаны, и по ним построен интервальный вариационный ряд. Пример: статистическому наблюдению подвергаются больницы области. Число больниц - 143. Вариационный признак - число коек. Строится интервальный ряд:
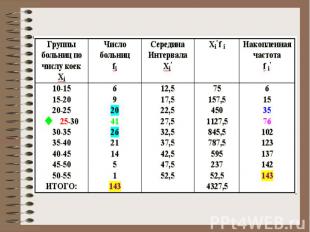

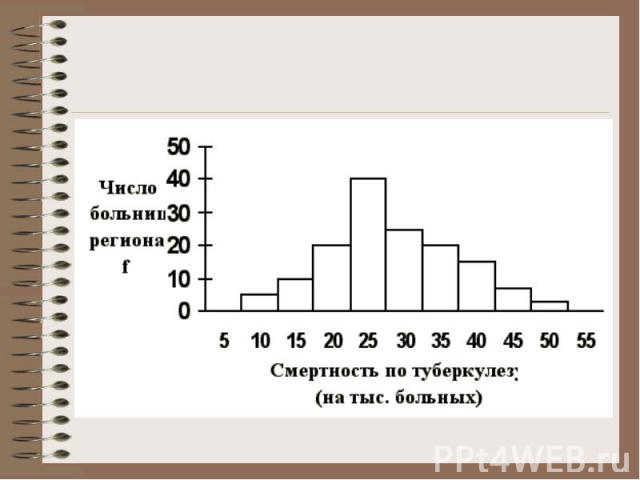
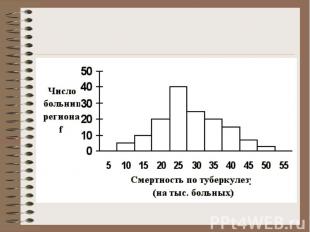
Предположим, что у нас нет в нашем распоряжении первичных данных. В этом случае мы не можем построить ранжированный вариационный ряд, как это было сделано в предыдущем примере. В нашем распоряжении есть только обработанные до нас данные, которые уже сведены к интервальному ряду. Например, интервальный ряд (в виде гистограммы) был взят нами из периодической литературы. Сами исходные данные не публиковались.

Медиана распределения вычисляется с использованием интервального ряда по формуле:


Квартили распределения Вычисляются абсолютно аналогично медиане по формулам:


Общее название для вышеприведенных структурных характеристик вариационного ряда - квантили. Если ряд делится на 4 части то в этом случае квантили называются квартилями (см. формулы выше), на 5 частей - квинтили ; на 10 - децили ; на 100 - перцентили .

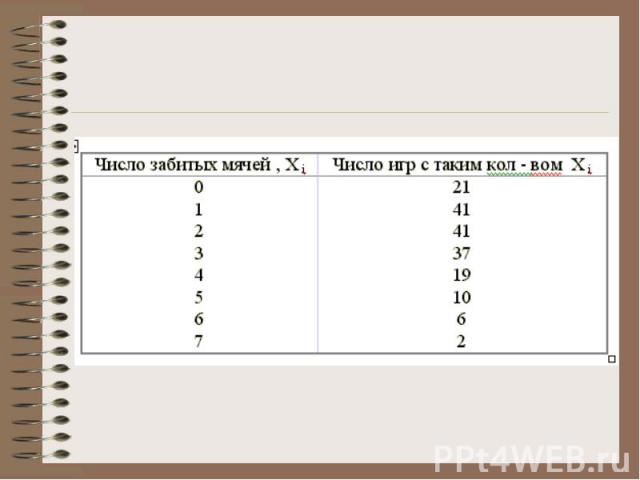
Мода распределения . Модальный интервал - интервал с наибольшей частотой .

Мода:
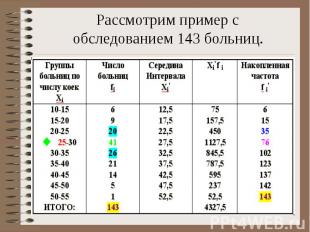
Рассмотрим пример с обследованием 143 больниц.

Рассмотрим пример с обследованием 143 больниц.