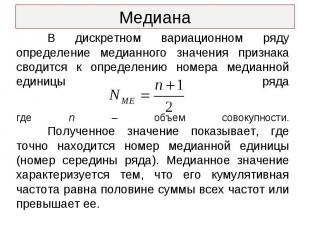
Презентация на тему: СРЕДНИЕ ВЕЛИЧИНЫ И ВАРИАЦИЯ

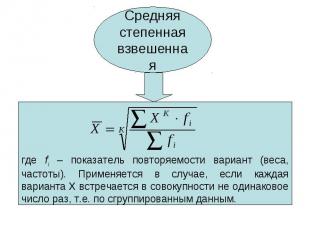
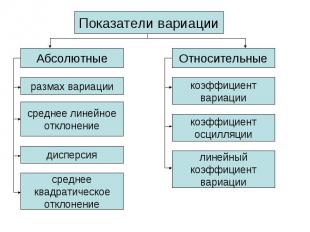
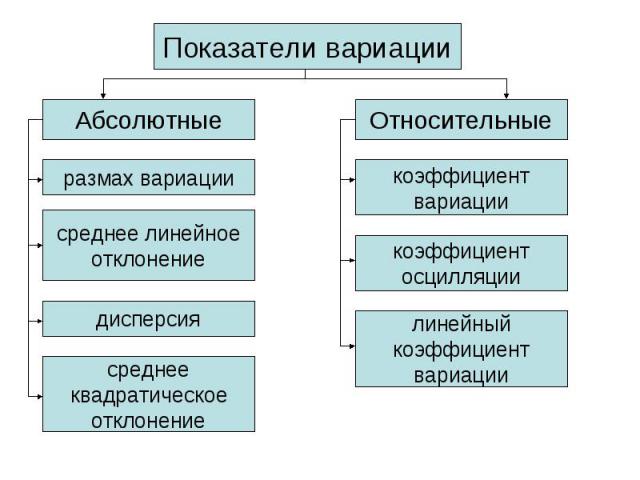
Характеристика границ вариации изучаемого признака. Определяется по формуле Характеристика границ вариации изучаемого признака. Определяется по формуле R= Xmax –Xmin , где Xmax- максимальное значение варьирующего признака; Xmin- минимальное значение варьирующего признака. Показывает, сколь велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признака, основан на крайних значениях варьирующего признака и не отражает отклонений всех вариант в ряду.

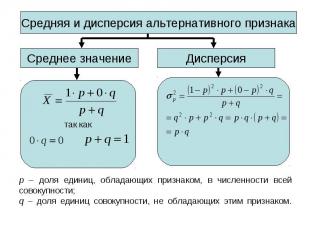
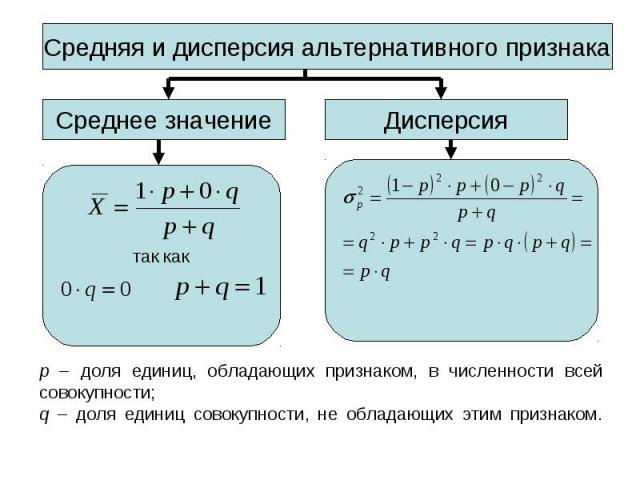
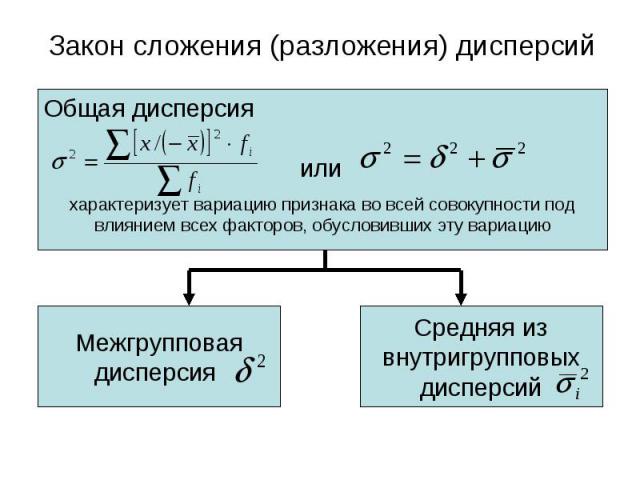
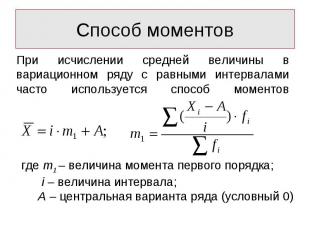
Средний квадрат отклонений индивидуальных значений признака от их средних величин. Вычисляется по следующим формулам: Средний квадрат отклонений индивидуальных значений признака от их средних величин. Вычисляется по следующим формулам: 1-й способ: или где Xi – индивидуальное значение варьирующего признака (варианты); - среднее значение варьирующего признака; n – количество разновидностей вариант; fi - показатель повторяемости вариант (частоты, веса).

Показывает на какую величину отклоняется признак в изучаемой совокупности от средней величины признака: Показывает на какую величину отклоняется признак в изучаемой совокупности от средней величины признака: Показатель рассчитывается по модулю.

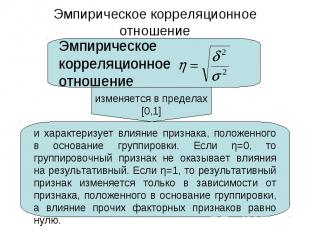
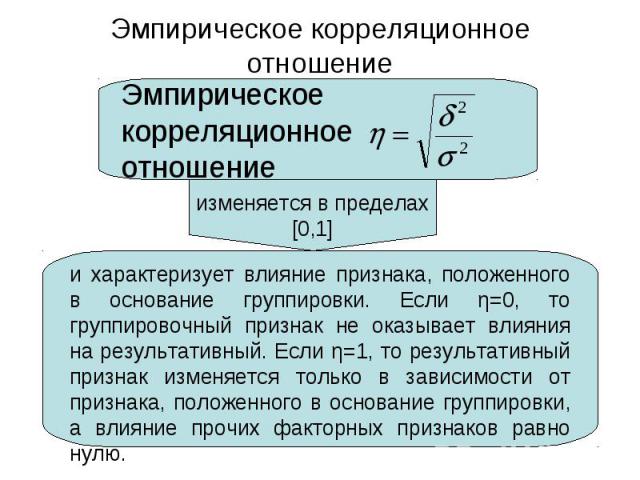
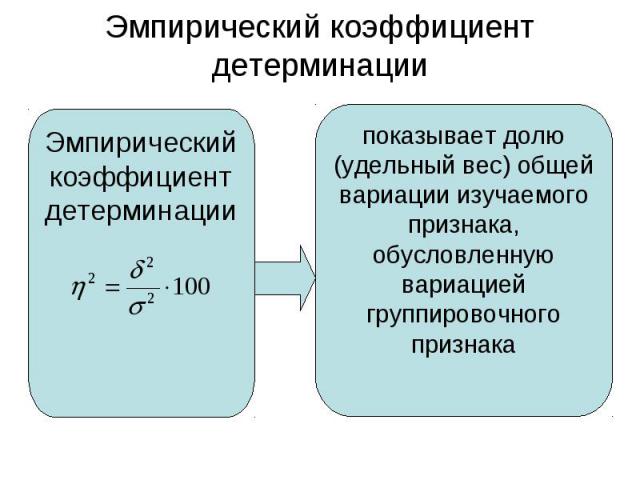
Характеристика меры вариации значений признака вокруг средней величины: Характеристика меры вариации значений признака вокруг средней величины: Чем этот показатель меньше, тем однороднее совокупность, а средняя величина признака типична для данной совокупности. Чем коэффициент вариации больше, тем неоднороднее совокупность.

Линейный коэффициент вариации: Линейный коэффициент вариации: Коэффициент осцилляции: