Презентация на тему: Решение ЕГЭ по математике

Как сдавать ЕГЭ по математике?1.Преодолеть минимальный порог , для того, чтобы получить аттестат, вам нужно сосредоточиться на заданиях В1,В2,В3,В5,В6 и В102.Если ваша цель-подтвердить свою школьную оценку и самооценку и получить высокий балл по математике для поступления в вуз, тогда ваш экзамен состоит из всех заданий части1(В1-В14) и заданий С1,С2.3.Если ваша цель - поступить в вуз на математическую специальность и вам нужен очень высокий балл на ЕГЭ, тогда вы должны уверенно решать все задания части1 и задания С1,С2,(как ни странно, наиболее подготовленные учащиеся часто ошибаются именно здесь ,по небрежности) Вам нужно уметь выполнять (может быть с некоторыми недочетами) задания С3и С4,С5,С6. Желаем удачи .!

Функция үзлекләрен тигезләмәләр һәмтигезссезлекләр чишүдә куллану .Математика укытучысы: Ситтигуллина Әлфия Борисовна

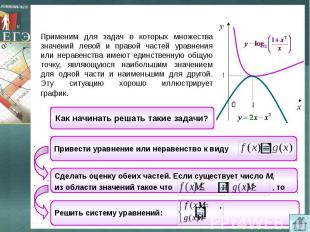
Применим для задач в которых множества значений левой и правой частей уравнения или неравенства имеют единственную общую точку, являющуюся наибольшим значением для одной части и наименьшим для другой. Эту ситуацию хорошо иллюстрирует график.       

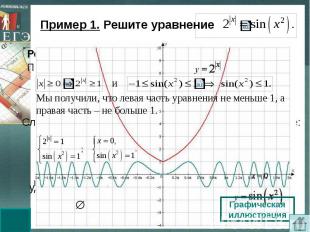
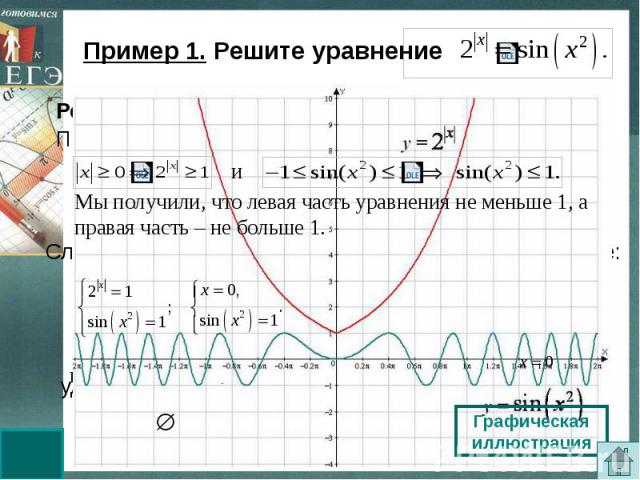
Пример 1. Решите уравнение Мы получили, что левая часть уравнения не меньше 1, а правая часть – не больше 1.

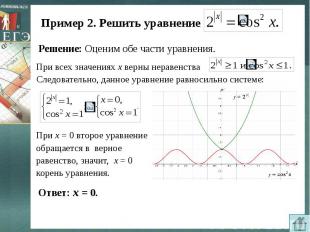
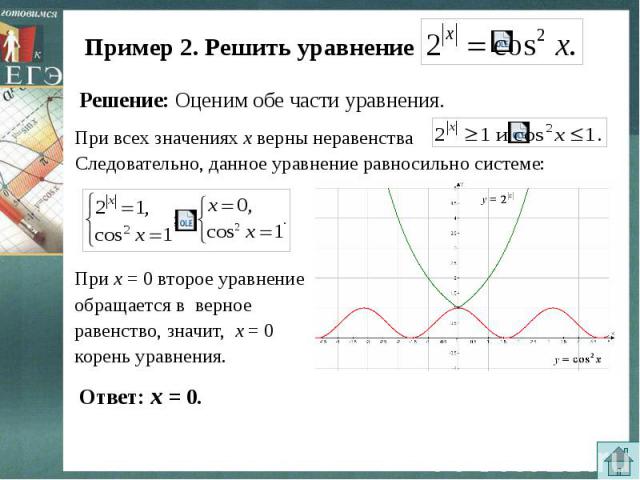
Пример 2. Решить уравнение Решение: Оценим обе части уравнения.При всех значениях х верны неравенстваСледовательно, данное уравнение равносильно системе:При х = 0 второе уравнение обращается в верное равенство, значит, х = 0 корень уравнения.

Пример 3. Решить неравенство Решение.Сделаем оценку функций, входящих в неравенство.Так как , то данная функция принимает наибольшее значение равное 1 при х = -1, значит, Следовательно, исходное неравенство выполняется тогда и только тогда, когда оба множителя равны 1 одновременно. Получаем х = -1 – единственное решение системы уравнений, а, значит, и данного неравенства.

Пример 5. Решить уравнение Решение. Оценим обе части уравнения. 1) Каждое слагаемое левой части уравнения не больше 1, следовательно их сумма будет равна 2, если они принимают своё наибольшее значение.

Пример 9. Решить уравнение Решение: Заметим, что х = 1 , является корнем данного уравнения. Левая часть уравнения представляет собой сумму двух возрастающих функций и, следовательно, сама является возрастающей функцией, принимающей каждое своё значение ровно один раз. Поэтому других корней данное уравнение не имеет.Ответ: 1.

Пример 10. Доказать, что уравнение не имеет решений:Арифметический корень не может быть отрицательным числом, поэтому уравнение решений не имеет.Левая часть исходного уравнения определена при , при каждом таком значении х Следовательно, их сумма всегда больше нуля. Не существует такого значения х, при котором оба выражения имеют смысл. Поэтому уравнение решений не имеет.ОДЗ уравнения:

ИСПОЛЬЗОВАНИЕ ОБЛАСТИ ОПРЕДЕЛЕНИЯ ФУНКЦИИ Решить уравнение:Решение. Итак, единственной точкой, в которой определены эти радикалы, является x = 1. Легко проверить, что это число – корень уравнения.

Решить уравнение Решение.1) Выпишем, условие существования функции, стоящей в левой части: Решить данное неравенство довольно сложно. 2) Проверим не отрицательность правой части: Последнее неравенство решений не имеет.3) Значит, исходное уравнение тоже не имеет решений, так как левая часть его – неотрицательная функция!

ИСПОЛЬЗОВАНИЕ СВОЙСТВА ОГРАНИЧЕННОСТИ ФУНКЦИИ ДЛЯ НАХОЖДЕНИЯ ЕЁ НАИБОЛЬШЕГО ЗНАЧЕНИЯУкажите наибольшее целое значение функцииРешение.Данная функция принимает наибольшее значение тогда и только тогда, когда наибольшее значение принимает функция, стоящая в показателе степени: Преобразуем её: