Презентация на тему: Решение задач по статике

Решение задач по статике Презентация подготовлена учителем физики школы №332Невского района города Санкт-ПетербургаТатьяной Викторовной Романовой

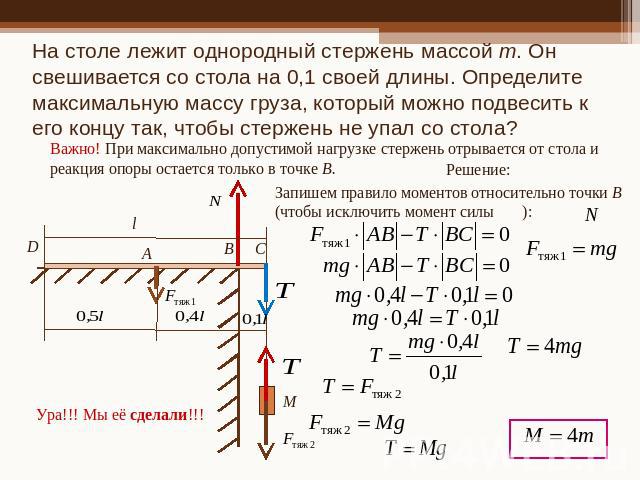
На столе лежит однородный стержень массой m. Он свешивается со стола на 0,1 своей длины. Определите максимальную массу груза, который можно подвесить к его концу так, чтобы стержень не упал со с тола? Важно! При максимально допустимой нагрузке стержень отрывается от стола и реакция опоры остается только в точке В.Запишем правило моментов относительно точки В (чтобы исключить момент силы ):

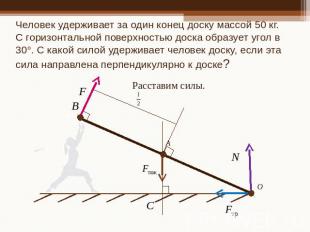
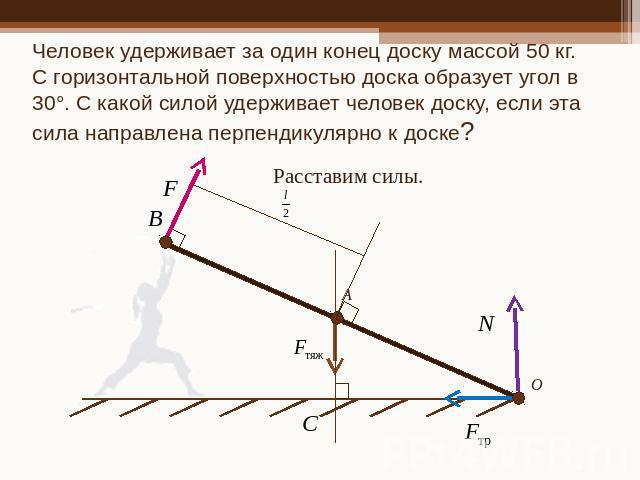
Человек удерживает за один конец доску массой 50 кг. С горизонтальной поверхностью доска образует угол в 30°. С какой силой удерживает человек доску, если эта сила направлена перпендикулярно к доске?

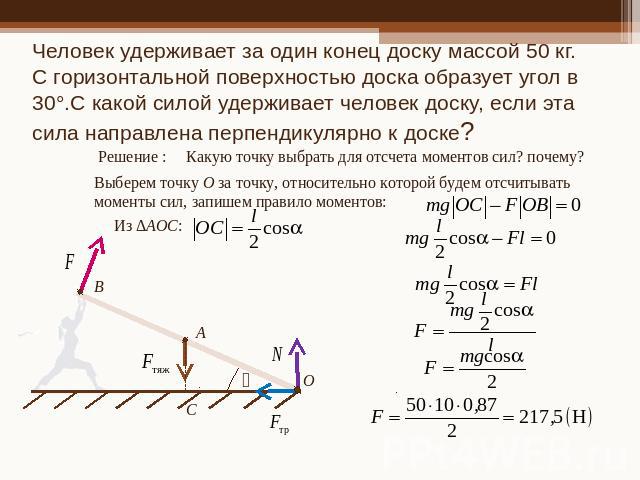
Человек удерживает за один конец доску массой 50 кг. С горизонтальной поверхностью доска образует угол в 30°.С какой силой удерживает человек доску, если эта сила направлена перпендикулярно к доске?

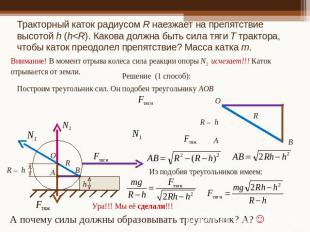
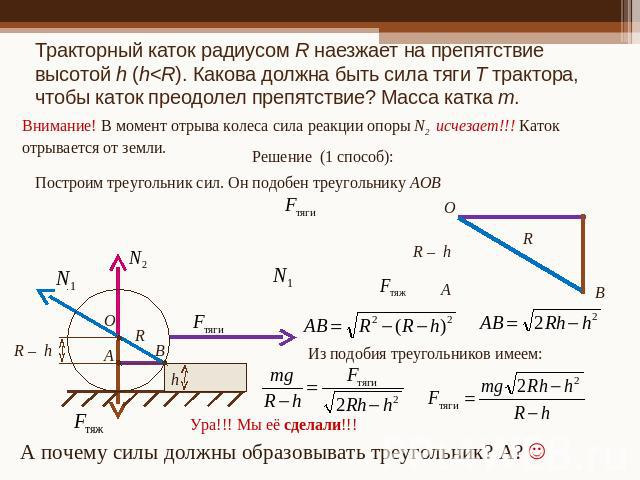
Тракторный каток радиусом R наезжает на препятствие высотой h (h<R). Какова должна быть сила тяги Т трактора, чтобы каток преодолел препятствие? Масса катка m.

Тракторный каток радиусом R наезжает на препятствие высотой h (h<R). Какова должна быть сила тяги Т трактора, чтобы каток преодолел препятствие? Масса катка m.

Лестница опирается на вертикальную стену и пол. При каких значениях угла между лестницей и полом она может стоять, если коэффициенты трения лестницы о пол и о стену равны μ1 и μ2 соответственно?

Решаем систему уравнений (1 – 3) относительно α

Лестница опирается на вертикальную стену и пол. При каких значениях угла между лестницей и полом она может стоять, если коэффициенты трения лестницы о пол и о стену равны μ1 и μ2 соответственно?

Решаем систему уравнений (1 – 3) относительно α

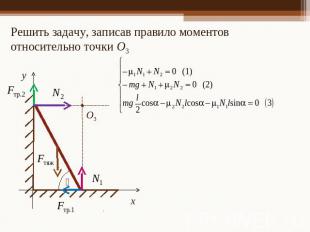
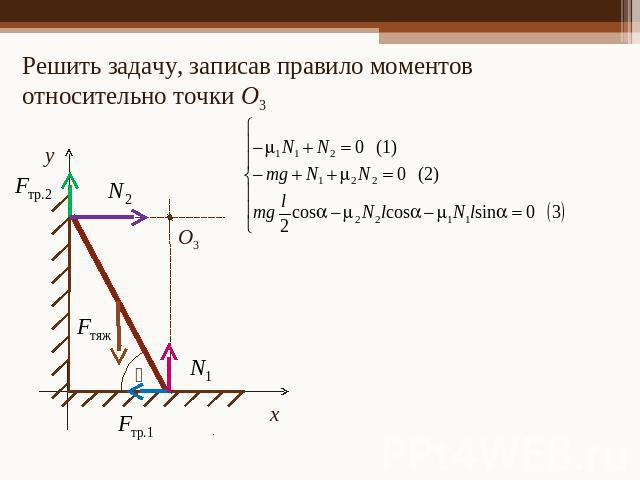
Решить задачу, записав правило моментов относительно точки О3

Решаем систему уравнений (1 – 3) относительно α

Вывод по задаче Выполняя рисунок, нужно начинать вектор силы точно в месте приложения , иначе можно неправильно определить плечо.В данной задаче не важно, какую точку взять для применения правила моментов. Каждая из трех выбранных точек убирает два момента сил, поэтому сложность решения любым из рассмотренных способов примерно одинакова. В других задачах надо постараться найти такую точку, которая убирает бόльшее число моментов тех сил, которые не просят найти. Тогда решение будет проще.

Решение задач на определение положения центра тяжести

В основе решения задач на определение центра тяжести лежит следующее обстоятельство: Если в центре тяжести частиц, жестко связанных друг с другом, приложить уравновешивающую силу, равную по модулю силе тяжести всех частиц, то система будет находится в равновесии.Сумма моментов всех сил, включая и уравновешивающую, должна быть равна нулю относительно любой точки.

Положение центра тяжести будем отсчитывать от крайней левой точки.

Пять шаров , массы которых равны соответственно m, 2m, 3m, 4m, 5m, укреплены на стержне так, что их центры находятся на расстоянии l друг от друга. Пренебрегая массой стержня, найдите центр тяжести системы.

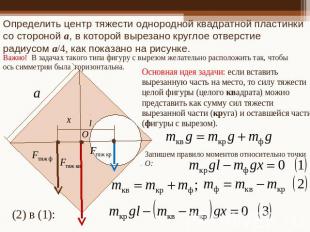
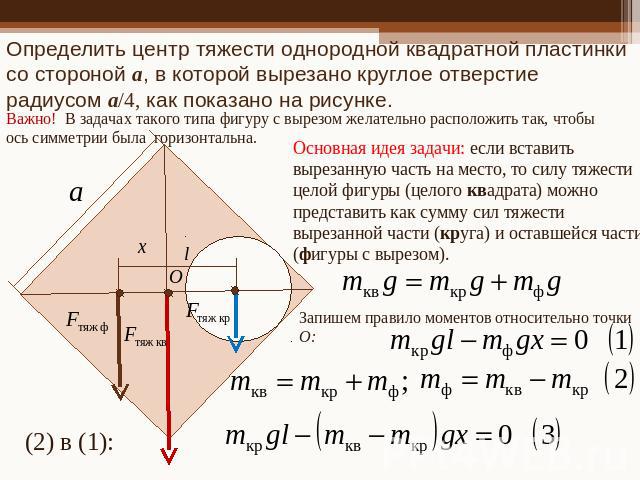
Определить центр тяжести однородной квадратной пластинки со стороной a, в которой вырезано круглое отверстие радиусом a/4, как показано на рисунке. Важно! В задачах такого типа фигуру с вырезом желательно расположить так, чтобы ось симметрии была горизонтальна.Основная идея задачи: если вставить вырезанную часть на место, то силу тяжести целой фигуры (целого квадрата) можно представить как сумму сил тяжести вырезанной части (круга) и оставшейся части (фигуры с вырезом).

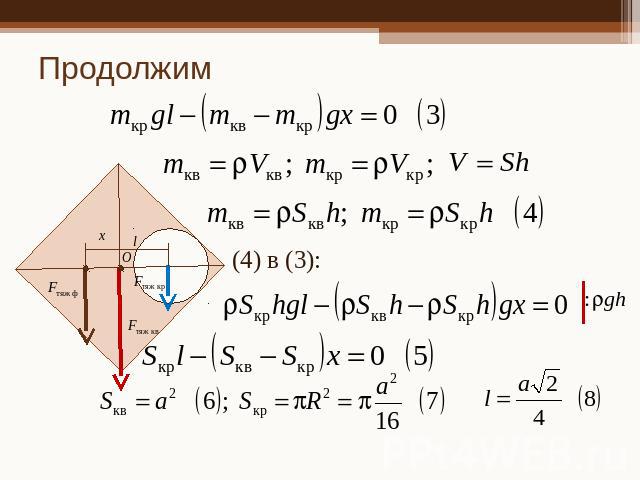
Продолжим

Ура!!! Мы и эту сделали!!!