Презентация на тему: Разложение вектора по двум неколлинеарным векторам. Координаты вектора

Разложение вектора по двум неколлинеарным векторам. Координаты вектора. 9 класс Федорищева Юлия Михайловна учитель математики МБОУ гимназия № 14 г. Ейска Краснодарского края Презентация из 15 слайдов: основные понятия, определения, поясняющие рисунки, алгоритм выполнения заданий

Разложение вектора по двум неколлинеарным векторам

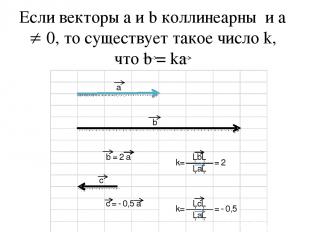
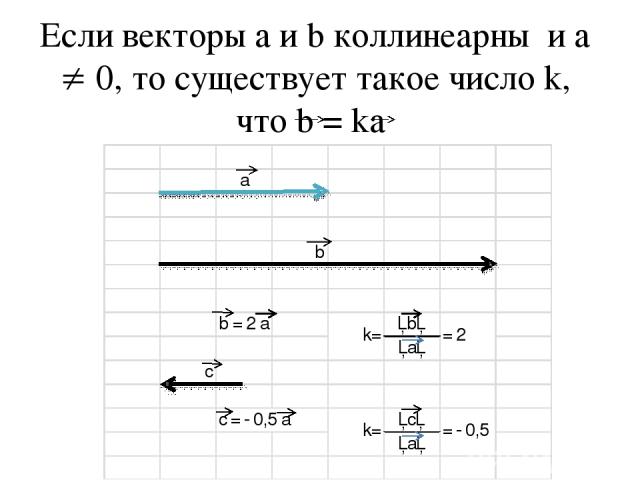
Если векторы а и b коллинеарны и а 0, то существует такое число k, что b = ka

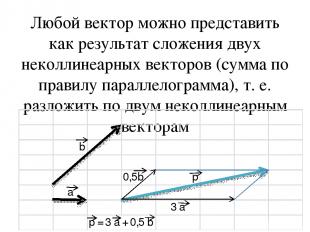
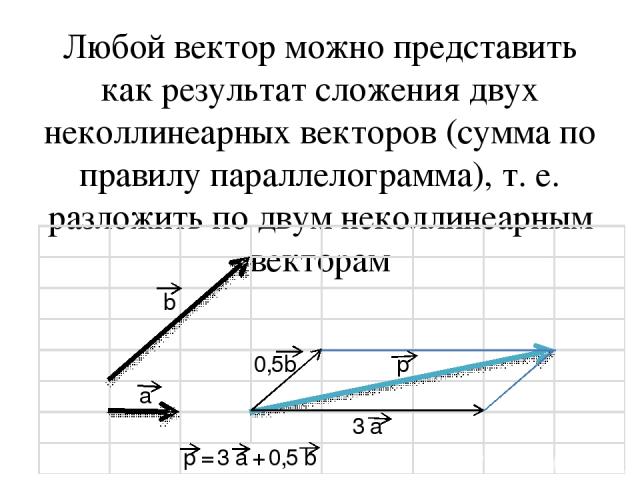
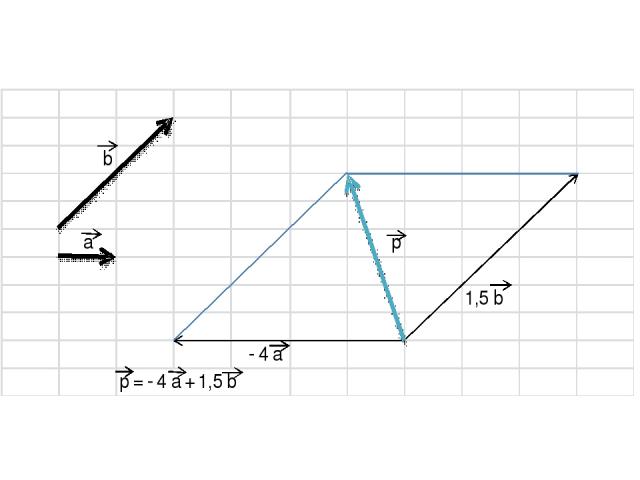
Любой вектор можно представить как результат сложения двух неколлинеарных векторов (сумма по правилу параллелограмма), т. е. разложить по двум неколлинеарным векторам

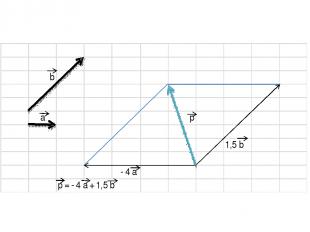
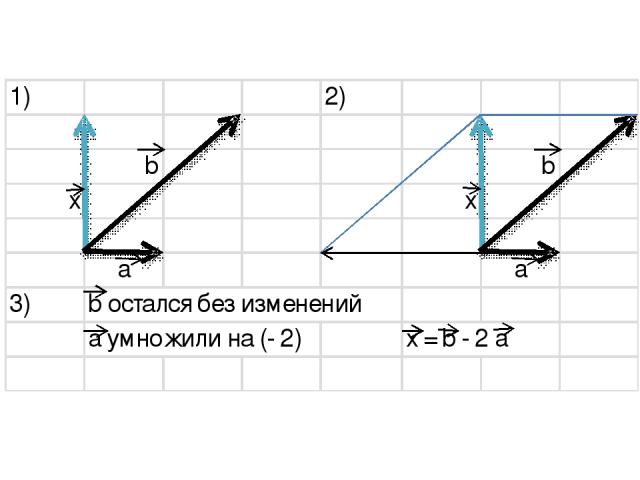
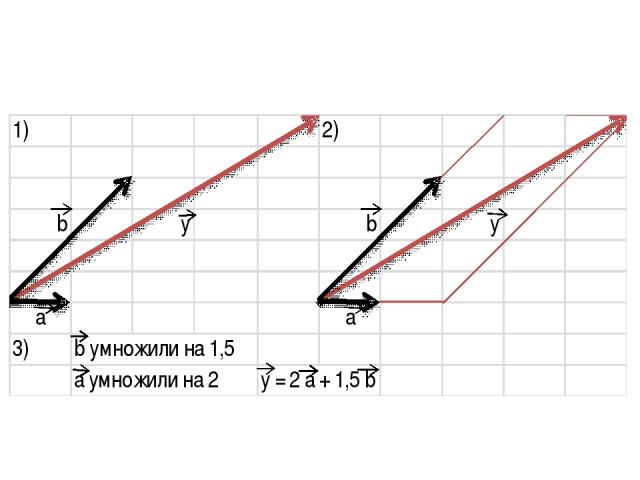
Чтобы разложить вектор по двум векторам надо: 1) отложить все три вектора от одной точки; 2) достроить до параллелограмма; 3) вычислить значения k для каждого вектора

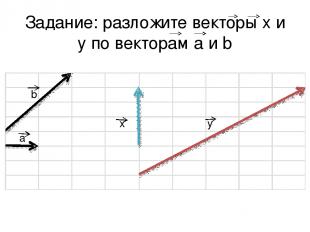
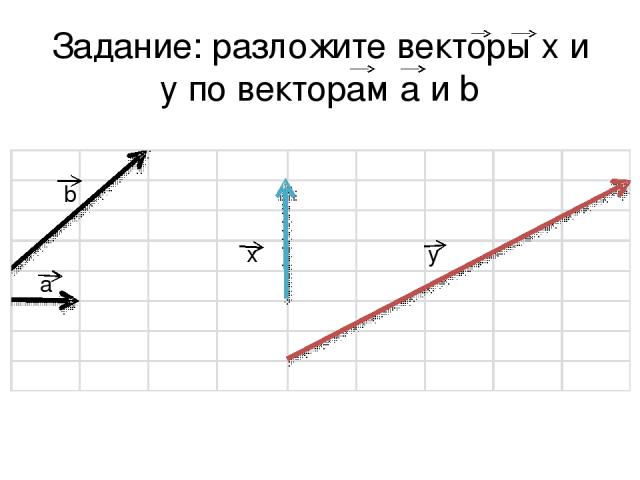
Задание: разложите векторы x и y по векторам a и b

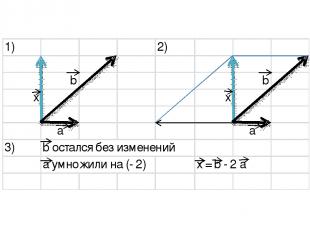
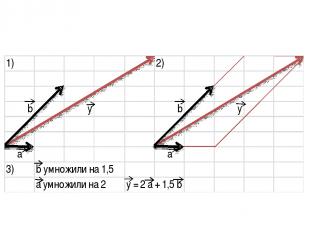
Координаты вектора

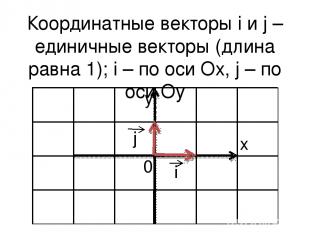
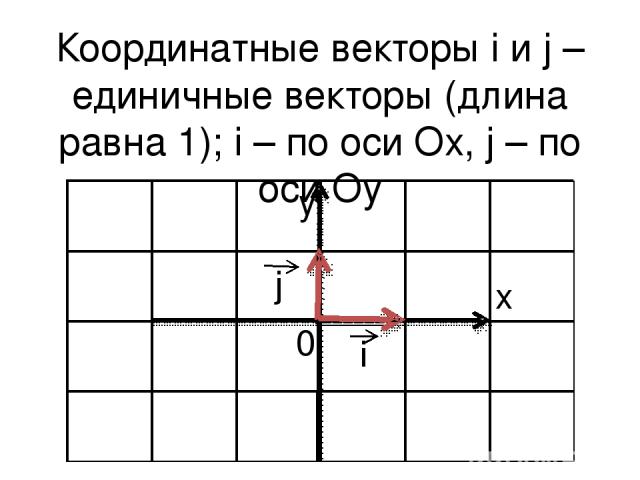
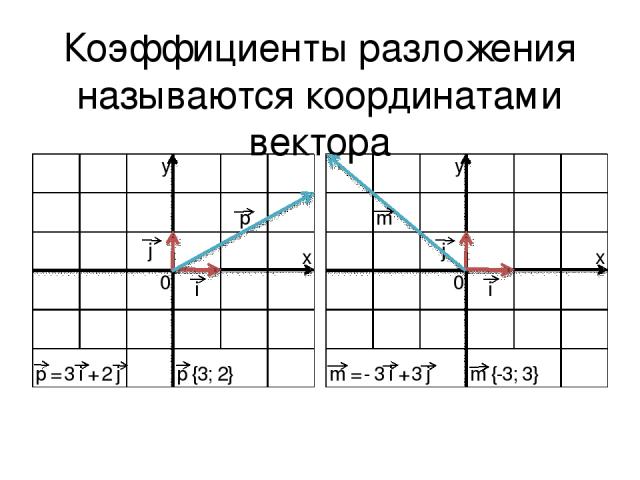
Координатные векторы i и j – единичные векторы (длина равна 1); i – по оси Ox, j – по оси Oy

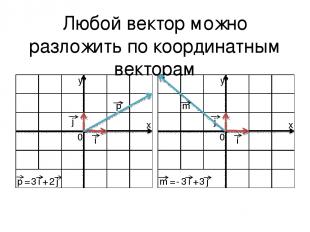
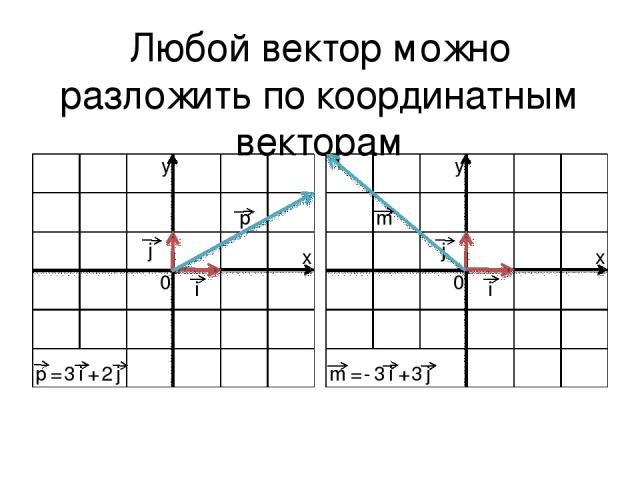
Любой вектор можно разложить по координатным векторам

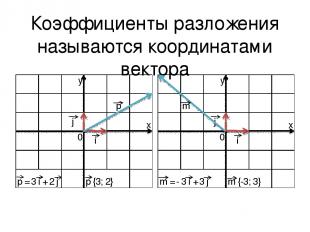
Коэффициенты разложения называются координатами вектора

1. Каждая координата суммы векторов равна сумме соответствующих координат a {2;3} + b {1;4} = c {3;7} 2. Каждая координата разности векторов равна разности соответствующих координат a {2;3} - b {1;4} = c {1;-1}

3. Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число если a {2;5}, то -4 a {-8;-20}

Задание: найти координаты вектора p = 2 a – 1/3 b + c, если a {1; -2}, b {0; 3}, c {-2; 3} 1) 2a {1*2; -2*2}, 2a {2; -4} 2) – 1/3b {0*(-1/3); 3*(-1/3)}, - 1/3 b {0; -1} 3) c {-2; 3} 4) p {2+0-2; -4-1+3}, p {0; -2}