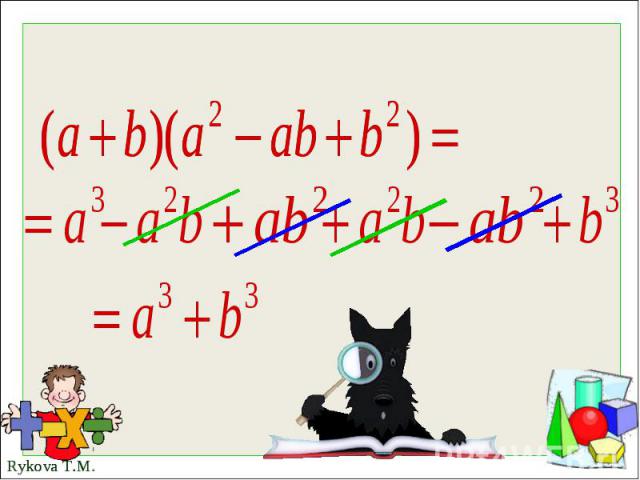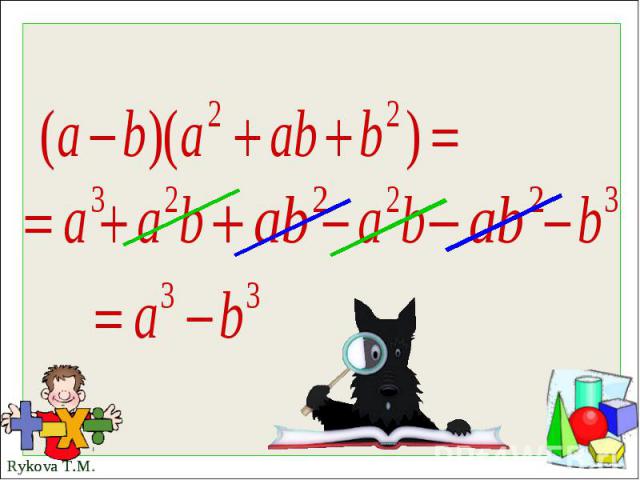Презентация на тему: Разложение на множители суммы и разности кубов

Разложение на множители суммы и разности кубов.

Цели урока: вывести формулы суммы и разности кубов; формировать умение применять их при разложении многочлена на множители

Устно: Представить в виде куба: 8х3 64с6 b12

Устно: Представить в виде куба: 125у3 x3 а9b6 8n6y15

Устно: Выполните возведение в квадрат. (2x – 1)2 (9 – n)2 (–3a + 5)2

Разложение на множители суммы и разности кубов.

Для разложения на множители суммы кубов используют тождество- формула суммы кубовДокажем ее.

Сумма кубов двух выражений равна произведению суммы этих выражений на неполный квадрат разности

Пример: Разложите на множители:

Для разложения на множители разности кубов используют тождество- формула разности кубовДокажем ее.

Разность кубов двух выражений равна произведению разности этих выражений на неполный квадрат суммы.

Пример: Разложите на множители:

Упражнения: № 905№ 907№ 909 (а, в, д)№ 911№ 912 (а, в, д)№ 914

Итоги урока: – Назовите формулы суммы и разности кубов.– Когда применяются эти формулы?– Какие ещё формулы позволяют разложить многочлен на множители? Назовите их.

Домашнее задание: П.36№ 906; № 908; № 910; № 912 (б, г, е).