Презентация на тему: Проекции перемещения на оси координат. Модуль перемещения

Проекции перемещения на оси координат. Модуль перемещения ГОУ ЦО № 133 учитель Е.В. Шаркова Использованы рисунки из презентации В.Е. Фрадкина «Векторные величины и действия с ними»

ПРОЕКЦИИ ПЕРЕМЕЩЕНИЯ НА ОСИ КООРДИНАТВспомним, как найти проекции вектора на оси координат: Для нахождения проекции вектора необходимо опустить перпендикуляры из начала вектора и из его конца на ось координат. Проекция вектора на ось координат – это отрезок на оси, заключенный между координатами конца и начала вектора.

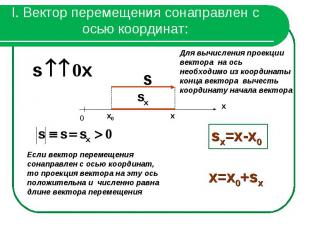
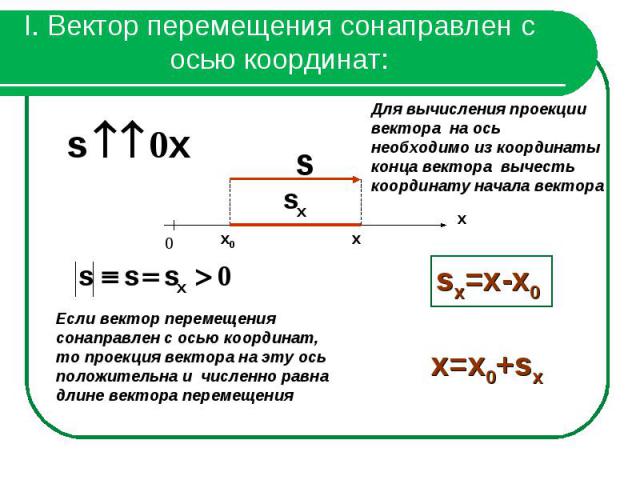
I. Вектор перемещения сонаправлен с осью координат:Для вычисления проекции вектора на ось необходимо из координаты конца вектора вычесть координату начала вектора Если вектор перемещения сонаправлен с осью координат, то проекция вектора на эту ось положительна и численно равна длине вектора перемещения

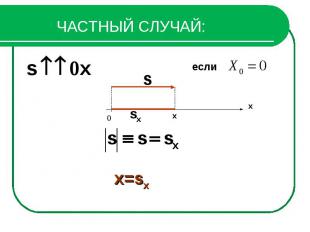
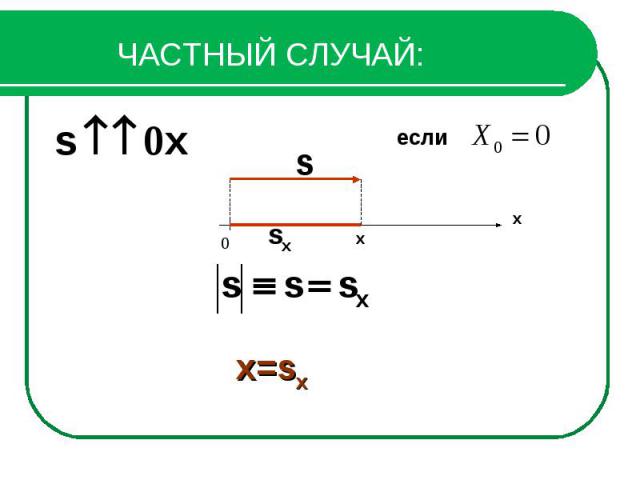
ЧАСТНЫЙ СЛУЧАЙ:

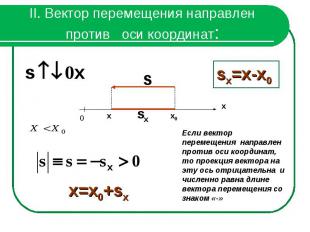
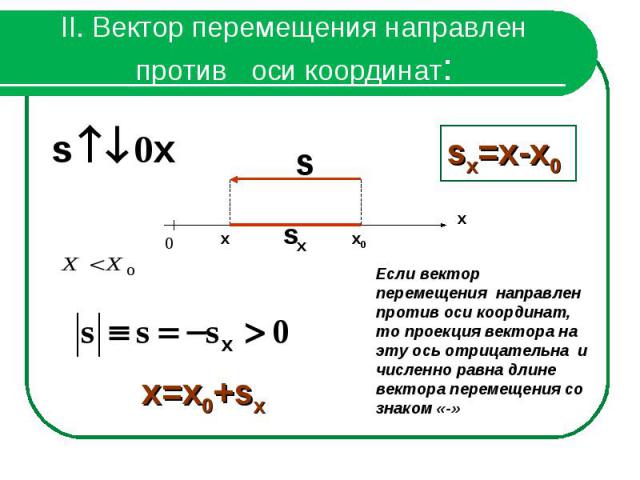
II. Вектор перемещения направлен против оси координат:Если вектор перемещения направлен против оси координат, то проекция вектора на эту ось отрицательна и численно равна длине вектора перемещения со знаком «-»

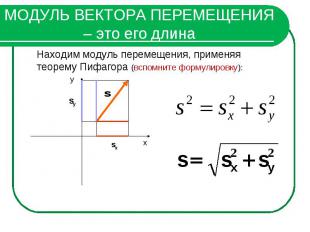
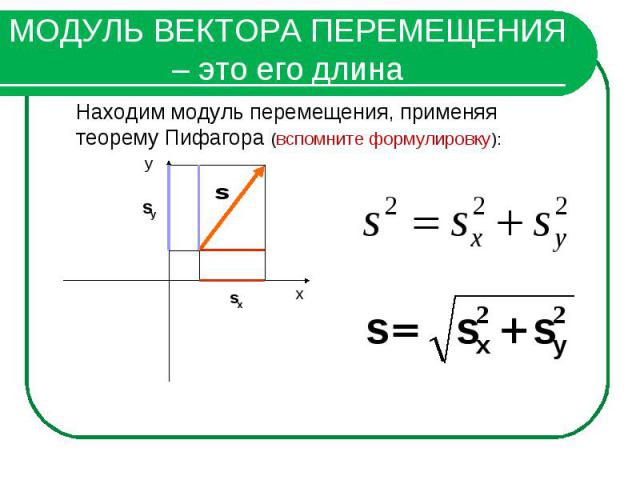
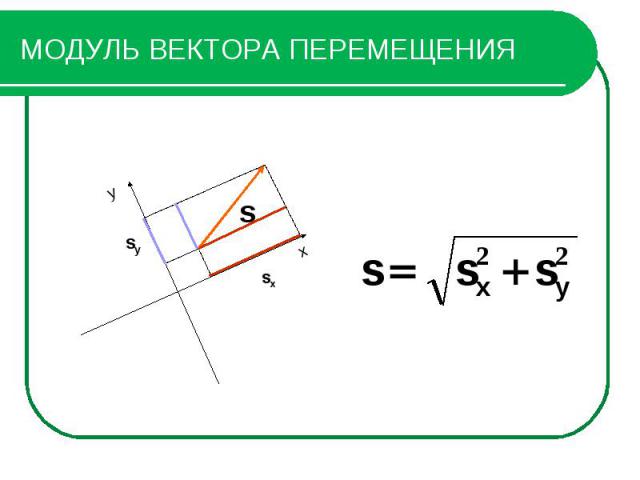
МОДУЛЬ ВЕКТОРА ПЕРЕМЕЩЕНИЯ – это его длинаНаходим модуль перемещения, применяя теорему Пифагора (вспомните формулировку):

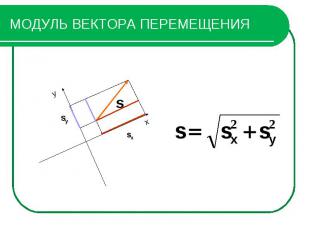
МОДУЛЬ ВЕКТОРА ПЕРЕМЕЩЕНИЯ

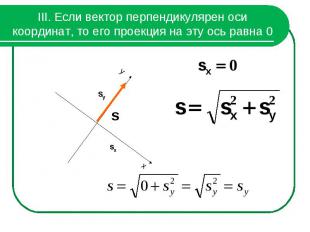
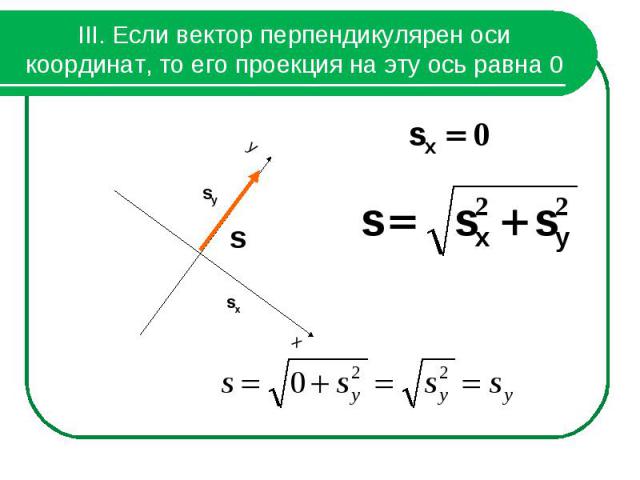
III. Если вектор перпендикулярен оси координат, то его проекция на эту ось равна 0