Презентация на тему: Правила по математике для начальных классов

ДРУЖОК Правила по математике для начальных классов

ЦИФРЫ И ЗНАКИ0 1 2 3 4 5 6 7 8 9Это арабские цифры. Их всего десять.I II III IV V VI VII VIII IX X …Это римские цифры. > больше + плюс < меньше - минус = равно или x умножение : деление

СРАВНЕНИЕ ЧИСЕЛ 3 > 2 2 < 3 3 = 3 1+2 < 4+3 5+3 > 7 4 < 5 < 7 Число 5 больше 4, но меньше 7.

ЧИСЛА ЧЁТНЫЕ И НЕЧЁТНЫЕ Числа, которые делятся на 2, называются ЧЁТНЫМИ: 2 4 6 8 10… Числа, которые не делятся на 2, называются НЕЧЁТНЫМИ: 1 3 5 7 9 11… При сложении чётных чисел получается чётное число, при сложении нечётных тоже получается чётное число: 4+2=6 3+5=8.Если складывают нечётное число с чётным, то в ответе будет нечётное число: 5+2=7.

СЛОЖЕНИЕ 5 + 2 = 7 первое второе сумма слагаемое слагаемое a + b = cПрибавить 1 к какому-либо числу – значит назвать следующее за ним по порядку число 1 2 3 4 5 6 7 8 9 . . . 6 + 1 = 7

ПЕРЕСТАНОВКА СЛАГАЕМЫХ От перестановки слагаемых сумма не изменяется a + b = b + aЕсли одно из слагаемых равно 0, то сумма равна другому слагаемому a + 0 = a 0 + a = a

ВЫЧИТАНИЕ 5 - 3 = 2 уменьшаемое вычитаемое разностьa – b = c Вычесть 1 из какого-либо числа – значит назвать предыдущее число 1 2 3 4 5 6 7 8 9 . . . 7 – 1 = 6

СОСТАВ ЧИСЛА 2 = 1 + 1 3 = 1 + 2 = 1 + 1 + 1 4 = 1 + 3 = 2 + 2 5 = 1 + 4 = 2 + 3 6 = 1 + 5 = 2 + 4 = 3 + 3 7 = 1 + 6 = 2 + 5 = 3 + 4 8 = 1 + 7 = 2 + 6 = 3 + 5 = 4 + 4 9 = 1 + 8 = 2 + 7 = 3 + 6 = 4 + 5

СЛОЖЕНИЕ И ВЫЧИТАНИЕчисел с переходом через десяток Одно из слагаемых надо разложить так, чтобы одна из промежуточных сумм была равна 10. 7+5=7+(3+2)=(7+3)+2= 10+2=12 Таким же способом можно решать примеры на вычитание 15-7= 15-(5+2)=(15-5)-2=10-2=8

ПОРЯДОК ВЫПОЛНЕНИЯ ДЕЙСТВИЙ ПРИ РЕШЕНИИ ВЫРАЖЕНИЙ СО СКОБКАМИ Прибавить число к сумме, а также сумму к числу можно, складывая числа в любом порядке (а + b) + c (a + b) + c = a + (b + c) (a + b) + c = (a + c) + b a + (b + c) a + (b + c) = (a + b) + c a + (b + c) = (a + c) + b

Вычесть из суммы число можно несколькими способами (a + b) – c(a + b) – c = (a – c) + b(a + b) – c = (b – c) + aЕсли перед скобкой в выражении стоит знак минус, то при раскрытии скобок знаки меняются на противоположныеa – (b + c) = a – b – ca – (b – c) = a – b + c

ПРОВЕРКА СЛОЖЕНИЯ Сложение можно проверить вычитанием. Для этого надо из суммы вычесть одно слагаемое. Если в результате получится другое слагаемое, значит сложение выполнено верно a + b = c c – a = b c – b = a

ПРОВЕРКА ВЫЧИТАНИЯ Вычитание можно проверить сложением. Для этого надо к разности прибавить вычитаемое. Если в результате получится уменьшаемое, значит вычитание выполнено верно a – b = c c + b = a

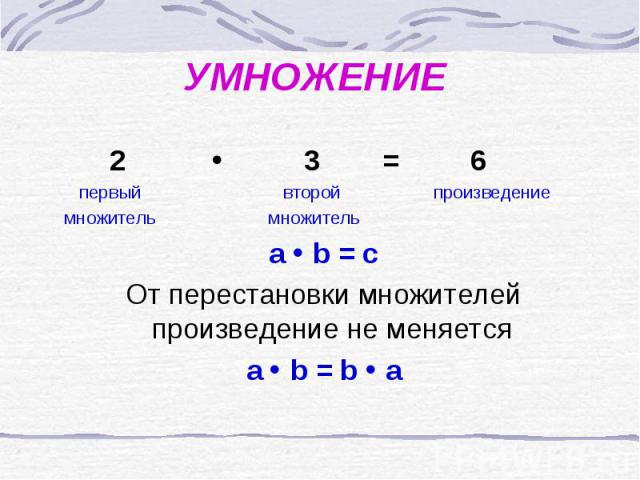
УМНОЖЕНИЕ 2 3 = 6 первый второй произведение множитель множитель a b = c От перестановки множителей произведение не меняется a b = b a

Если один из множителей равен 0, то произведение равно 0. a 0 = 0 0 a = 0 Если один из множителей равен 1, то произведение равно другому множителю а 1 = а 1 а = а

Умножение суммы на число (a + b) c (a + b) c = a c + b c a (b + c) a (b + c) = a b + a c

Проверка умножения - делени Если произведение двух чисел разделить на один из множителей, то получится другой множитель a b = c c : b = a c : a = bе

ДЕЛЕНИЕ : 3 = 2 делимое делитель частное a : b = cЕсли делитель равен 1, то частное равно делимомуа : 1 = аЕсли делимое равно делителю, то частное равно 1а : а = 1Если делимое равно 0, то частное равно 00 : а = 0Делить на 0 нельзя! а : 0

ПРИЗНАКИ ДЕЛИМОСТИ ЧИСЕЛ На 2 делятся числа, оканчивающиеся на чётную цифру: 28:2=14 174:2=87 На 3 делятся числа, сумма цифр которых делится на 3: 225:3=75 (2+2+5=9. Число 9 делится на 3) На 4 делятся числа, если двузначное число, образованное двумя последними цифрами, делится на 4: 216:4=54 (две последние цифры делимого составляют число 16, которое делится на 4)На 5 делятся числа, оканчивающиеся на 5 или 0: 70:5=14 145:5=29

ДЕЛЕНИЕ СУММЫ НА ЧИСЛОДЕЛЕНИЕ ЧИСЛА НА ПРОИЗВЕДЕНИЕ

ПРОВЕРКА ДЕЛЕНИЯ Если делимое разделить на частное, получится делитель а : b = c Проверка: а : с = b Если делитель умножить на частное, получится делимое a : b = c Проверка: с b = a

ДЕЛЕНИЕ С ОСТАТКОМ Если делимое не делится на делитель, например 7 : 3, то надо подобрать ближайшее число, меньше 7, которое делится на 3 без остатка7:3(6+1):36:3+12 (остаток 1) Остаток всегда должен быть меньше деления.

ЗАПОМНИ Увеличить число на несколько единиц – значит прибавить a + b Увеличить число в несколько раз – значит умножить a b Уменьшить число на несколько единиц – значит вычесть a – bУменьшить число в несколько раз – значит разделить а : b

РЕШЕНИЕ УРАВНЕНИЙ Неизвестное число обозначается латинской буквой Х Х + а = с а – Х = с Х = с – а Х = а – сХ с = а с : Х = аХ = а : с Х = с : а

ПЕРИМЕТР ФИГУРЫ Периметр – это сумма сторон геометрических фигур (квадрата, прямоугольника и т. д.), обозначается латинской буквой Р. Единицы измерения – миллиметры (мм), сантиметры (см), метры (м). Периметр прямоугольника Р = a+b+a+b = 2 a+2 b = 2 (a+b) Периметр квадратаР = а + а + а + а = 4 аПериметр треугольникаР = a + b + c

ПЛОЩАДЬ ФИГУРЫ Площадь – это внутренняя часть фигуры (прямоугольника, квадрата и т. д.), обозначается латинской буквой S. Единицы измерения – квадратные километры (км²), квадратные метры (м²), квадратные сантиметры (см²). Площадь прямоугольника S = a b Площадь квадрата S = a a