Презентация на тему: Пифагор Самосский

Выяснить, фамилия какого ученого зашифрована в математических примерах. Г 0,5625 *2,4 = 1,35 Ф 0,6156:1,9= 0,324 И 121,4-29,7= 91,7 П 132,96+21,4 =154,36 А (8,75+3,6) *6,9= 85,215 Р 7,04:5 +5,624:9,5 = 2 О (11,76-9,36)*0,5051, =1,21224 1,212 154,36 91,7 0,324 85,215 1,35 1,212 2 П и ф а г о р

Пифагор Самосский

Да, я Пифагор. Родился около 570 г. до н. э. На самосском острове Я посетил множество стран и учился у многих мыслителей того времени.

Что открыл Пифагор? «Геометрия владеет двумя сокровищами: одно из них – это теорема Пифагора»Обо мне сохранились десятки легенд и мифов, с моим именем связано многое в математике, и в первую очередь, конечно, теорема носящая моё имя, которая занимает важнейшее место в школьном курсе геометрии.

Когда впервые заговорили об этом открытии?Как утверждают все античные авторы, Пифагор первый дал полноценное доказательство теоремы, носящей его имя. К сожалению, мы не знаем, в чем оно состояло, потому что древние математики и писатели об этом умалчивают, а от самого Пифагора и ранних пифагорейцев до нас не дошло ни одного письменного документа. В настоящее время известно, что эта теорема не была открыта Пифагором. Однако одни полагают, что Пифагор первым дал ее полноценное доказательство, а другие отказывают ему и в этой заслуге. Некоторые приписывают Пифагору доказательство, которое Евклид приводит в первой книге своих "Начал"

Формулировки теоремы Пифагора различны. Общепринятой считается следующая:«В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».Во времена Пифагора формулировка теоремы звучала так:«Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на катетах».


Доказательство теоремы считалось в кругах учащихся средних веков очень трудным и называлось: «Dons asinorum»-«ослиный мост» или“elefuga” - «бегство убогих» а сама теорема –«ветряной мельницей», «теоремой – бабочкой» или «теоремой невесты»Сейчас известно около 150 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.)


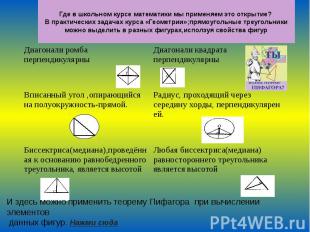
Где в школьном курсе математики мы применяем это открытие? В практических задачах курса «Геометрии»;прямоугольные треугольники можно выделить в разных фигурах,исползуя свойства фигур И здесь можно применить теорему Пифагора при вычислении элементов данных фигур. Нажми сюда

С глубокой древности математики находят все новые и новые доказательства теоремы Пифагора, все новые и новые замыслы ее доказательств. Таких доказательств – более или менее строгих, более или менее наглядных – известно более полутора сотен (по другим источникам, более пятисот), но стремление к преумножению их числа сохранилось. Поэтому теорема Пифагора занесена в «Книгу рекордов Гиннеса». Самостоятельное «открытие» доказательства теоремы Пифагора будет полезно и современным школьникам.
























