Презентация на тему: Решение задач на смеси, сплавы, растворы

Решение задач на смеси, сплавы, растворы.Обучающий проект по решению задач в 8-9 классах Подготовила: учитель математики МОУ кадетской школы Шалдохина Н.В

При решении таких задач важно знать, что:1%−это сотая часть рассматриваемой величины (52% от х кг − это 0,52х кг);Если в смеси растворов объемом V (массой m) нас интересует компонент объемом V0 (массой m0), то процентное содержание этого вещества можно просчитать по формуле: P0=(V0/V)∙100% или P0=(m0/m) ∙100% ;В качестве неизвестных обычно выбирают объемы или массы компонентов смеси (сплава);Складывать, уравнивать, сравнивать можно только массовые доли одного и того же вещества, или веществ в смеси (сплаве).

Смешали 30 %-ный раствор соляной кислоты с 10 %-ным раствором и получили 600 г 15 %-ного раствора. Сколько граммов каждого раствора было взято?0,3Х+0,1(600−Х)=0,15∙600, Х=150150 г первого раствора, тогда 600−150=450(г) второго раствора.

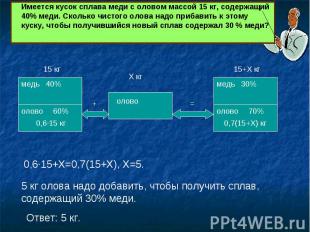
Имеется кусок сплава меди с оловом массой 15 кг, содержащий 40% меди. Сколько чистого олова надо прибавить к этому куску, чтобы получившийся новый сплав содержал 30 % меди?5 кг олова надо добавить, чтобы получить сплав, содержащий 30% меди.

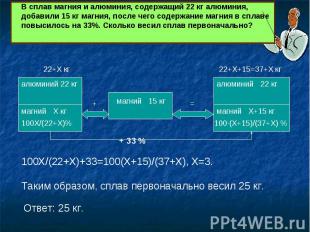
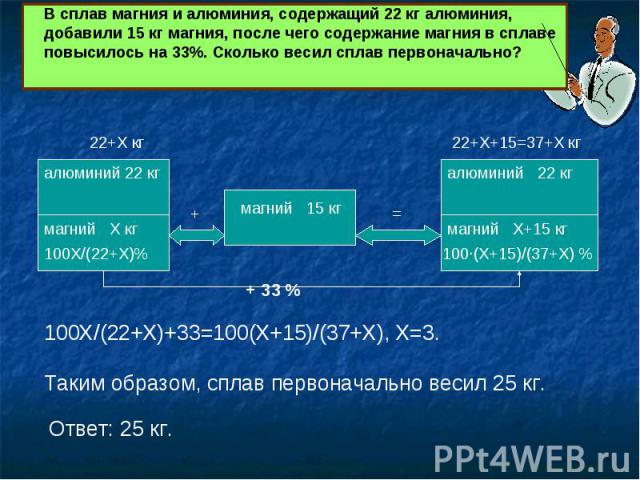
В сплав магния и алюминия, содержащий 22 кг алюминия, добавили 15 кг магния, после чего содержание магния в сплаве повысилось на 33%. Сколько весил сплав первоначально?Таким образом, сплав первоначально весил 25 кг.

Смесь, состоящая из двух веществ, весит 18 кг. После того, как из нее выделили 40 % первого вещества и 25 % второго, в ней первого вещества стало столько же, сколько второго. Сколько каждого вещества было в смеси?1-го вещества было 10 кг, а 2-го вещества было 8 кг.

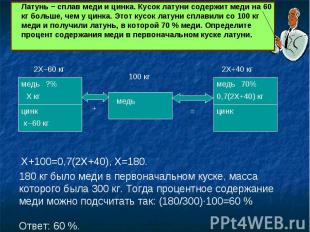
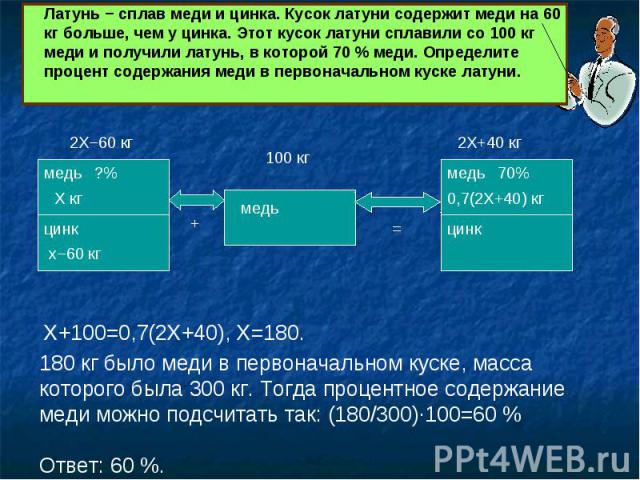
Латунь − сплав меди и цинка. Кусок латуни содержит меди на 60 кг больше, чем у цинка. Этот кусок латуни сплавили со 100 кг меди и получили латунь, в которой 70 % меди. Определите процент содержания меди в первоначальном куске латуни. 180 кг было меди в первоначальном куске, масса которого была 300 кг. Тогда процентное содержание меди можно подсчитать так: (180/300)∙100=60 %

Для приготовления лекарства потребовался 76 %-ный спирт. Провизор налил в колбу 220 г 95 %-ного спирта. Затем он отлил некоторое количество спирта и добавил в колбу столько же воды. Сколько грамм воды добавил провизор?

Имеется два сплава с разным содержанием золота. В первом сплаве содержится 35%, а во втором – 60% золота. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 40% золота?Таким образом, Х:У=4:1