Презентация на тему: Общая начальная математическая подготовка в 1 – 5 классах

Общая начальная математическая подготовка в 1 – 5 классах ТМОМ Общепедагогические основы обучения математике

План 1. Основные вопросы курса математики в начальной школе.2. Преемственность в изучении математики в 5 классах.

Начальный курс математики Интегрированный курс, в котором объединены арифметический, алгебраический и геометрический материалы. Его основу составляют представления о натуральном числе и нуле, четырех арифметических действиях с целыми неотрицательными числами и важнейших их свойствах, ознакомление с величинами и их измерением, осознанное и прочное усвоение приемов устных и письменных вычислений.

Основной принцип построения начального курса математики концентрическое построение курса математики, связанное с последовательным расширением области чисел.

Ведущие принципы обучения математике в младших классах учет возрастных особенностей учащихся; органическое сочетание обучения и воспитания; усвоение знаний и развитие познавательных способностей детей;практическая направленность обучения

Основные вопросы начального курса математики Понятие о натуральном числе и арифметических действияхИзучение сложения и вычитания в пределах 10Многозначные числаПравила о порядке выполнения арифметических действийРешение задачПонятие величиныГеометрический материалЭлементы алгебраической пропедевтики

Понятие о натуральном числе и арифметических действиях Начинается с первых уроков. На примере чисел первого десятка выясняется, как образуется каждое следующее число в натуральном ряду, устанавливается соотношение между любым числом ряда и всеми предшествующими или последующими числами, учащиеся знакомятся с различными способами сравнения чисел (сначала на основе сравнения соответствующих групп предметов, а затем по месту, которое занимают сравниваемые числа в ряду)

Понятие о натуральном числе и арифметических действиях 1. Изучение сложения и вычитания - знакомство с названиями действий, их компонентов и результатов, терминами равенство, неравенство ;усвоение элементов математической символики: знаков действий (плюс, минус), знаков отношений (больше, меньше, равно); чтение и запись математических выражений вида 6+ (6 - 2);нахождение значений выражений; знакомство со связью взаимно обратных операций;обучение письменным вычислениям.

Пример задачи на устанавление связи операций сложения и вычитания, их последовательности с предметными практическими действиями (В.В.Давыдов)№246. Решали три задачи о грушах в 2-х ящиках и получили такие записи:31-8; 31+(31-8); 31+(31+8). Составь полное условие к каждой задаче. Вычисли ответы.Пример задачи на выявление значения понятий множителя, делителя, делимого №407. Какие уравнения решаются делением. Реши только их.х*а=18; 12:х=t; x:d=5; x:3=15; b*x=7

Пример задач на составления модели уравнения, знаковой фиксации отношения делимости для нахождения заданной части целого и количества данных частей в целом. (В.В.Давыдов)№415. Посчитайте количество клеточек в узоре удобным способом.Пример задачи на выявление значения понятий множителя, делителя, делимого №416. Определи по записям, какими двумя способами считали крестики: (9*4)+(2*4); 11*4.

Понятие о натуральном числе и арифметических действиях 2. Многозначные числавыполнение арифметических действий в пределах миллиона на основе применения приема алгоритмизации (осуществляется своевременный переход от подробного объяснения каждого шага рассуждений к постепенному свертыванию объяснений, когда выделяются только основные элементы алгоритма. Например: "Делю тысячи, получаю...", "Делю сотни, получаю...", "Делю десятки, получаю..." и т. д. );- усложнение действий со скобками.

Решение задач Типы задач :– простые текстовые задачи (задачи, решаемые одним действием) способствуют более осознанному усвоению детьми смысла самих действий. на простых текстовых задачах дети знакомятся и со связью между такими величинами, как цена - количество - стоимость; норма расхода материала на 1 вещь – число изготовленных вещей и общий расход материала; скорость – время – пройденный путь при равномерном движении и т.д.;– составные задачи небольшой сложности (например, в 2 действия), направленные главным образом на разъяснение рассматриваемых свойств действий, на сопоставление различных случаев применения одного и того же действия, противопоставление случаев, требующих применения различных действий.

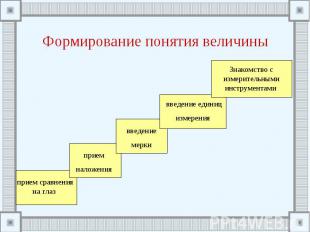
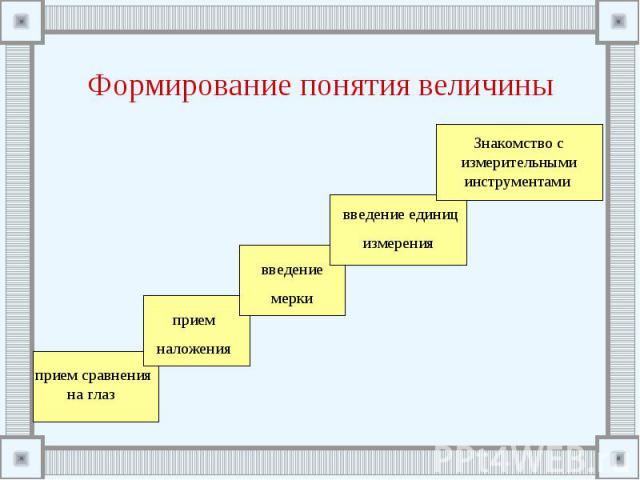
Формирование понятия величины

Изучение геометрического материала 1. Формирование представлений о геометрических фигурах (точка, линии (кривая, прямая), отрезок, ломаная, многоугольники различных видов и их элементы (углы, вершины, стороны), круг, окружность и др.) .2. Развитие геометрической «зоркости» (умения распознавать геометрические фигуры на сложном чертеже, составлять заданные геометрические фигуры из частей и др.). 3. Измерение длины отрезка, решение задач на нахождение суммы и разности двух отрезков, длины ломаной, периметра многоугольника и в том числе прямоугольника (квадрата), а в дальнейшем и площади прямоугольника (квадрата).

Основные цели изучения геометрического материала 1) развитие пространственного мышления учащихся как разновидность образного;2) познание окружающего ребенка мира с геометрических позиций как базы создания учащимися геометрической картины мира. Развитие умения использовать сформированные представления при ориентации в окружающем ребенка мире;3) развитие рефлексивных способностей учащихся;4) подготовка к сознательному усвоению курса геометрии в 7-11классах к изучению смежных дисциплин;

Основные цели изучения геометрического материала 5) формирование представлений о геометрических фигурах и отношениях. Эти представления образуют объемы понятий фигур, изучаемых в основной и старшей школе, и отношений (принадлежности, пересечения, перпендикулярности, параллельности), являются базой понятий, т.е. фактически готовят введение собственно понятий;6) развитие конструктивных умений в выполнении построения циркулем, линейкой, угольником, транспортиром;7) формирование навыков измерения геометрических величин;8) формирование умений конструировать определения геометрических объектов. Ознакомление с простейшими дедуктивными обоснованиями;9) развитие вербально-логического мышления. Формирование умений выделять существенные свойства фигур, конструировать описания геометрических объектов, четко формулировать выводы на основе наблюдений.

Элементы алгебраической пропедевтики Ознакомление с понятием переменной, введение буквенного обозначенияТема "Числа от 1 до 10" : значения слагаемых заданы в табличной форме. Найти суммы и заполнить соответствующие клетки таблицы. Примеры с окошком: *-8 = 56, ^ + 9=19, лс:4 = 7 (ознакомление с уравнениями)Формирование обобщений в виде формул (4 класс): -Ь = Ь, а-1=а, 0-^ = 0, Ь-0 = 0

Особенности начального курса математики Обучение в тесной связи с жизнью .Основные понятия, отношения, взаимосвязи, закономерности раскрываются на системе соответствующих конкретных задач. Изучение геометрического материала носит иллюстративный характер. Его основной функцией является обеспечение наглядности. Осуществление алгебраической пропедевтики.

Преемственность в изучении математики в 5 классах Развитие линии числа1. Систематизация и расширение сведений о натуральном и дробном числе, полученных в начальной школе с опорой на позиционное представление числа. Три приема для мотивации изучения дробных чисел:измерение величины;разрешимость уравнений;выполнимость действий 2. В 5 классе законы арифметических действий записываются в общем виде с использованием буквенной символики. Рассмотрение коммуникативного и ассоциативного законов умножения целесообразно связать с геометрическим материалом, а именно с вычислением площадей прямоугольников и объемов прямоугольных параллелепипедов.

Преемственность в изучении математики в 5 классах Пропедевтика курса алгебры в 5-6 классах:Введение алгебраической символики.Знакомство с возможностями, которые открываются при использовании букв.Накопление опыта работы с алгебраическим языком.

Преемственность в изучении математики в 5 классах В 4 – 5 классах в процессе изучения геометрического материала:1) уточняются и углубляются представления о геометрических объектах и их свойствах, приобретенные при обучении 1-3 классах;2) вводятся новые геометрические фигуры (луч, параллельные прямые, биссектриса угла и т.д.), некоторые преобразования фигур;3) изучаются новые величины, носителями которых являются знакомые фигуры (например, длина окружности, величина угла), проводится четкое различие величин и фигур (например, отрезок и длина отрезка, угол и градусная мера угла);4) расширяется круг геометрических построений и используемых при этом инструментов.

Благодарю за внимание!