Презентация на тему: Метод мажорант

ФЕСТИВАЛЬ ИССЛЕДОВАТЕЛЬСКИХ И ТВОРЧЕСКИХ РАБОТУЧАЩИХСЯ «ПОРТФОЛИО»«Метод мажорант»Работа ученицы 11 «А» классаГосударственного образовательного учреждения лицея №1571 Северо-Западного окружного управления Департамента образования города Москвы Кисловой АнныНаучный руководитель учитель математикилицея №1571 Свежевская Ольга ГеннадьевнаНаучный консультант учитель математики Бохонова Клавдия Васильевна, Заслуженный учитель России2007 год

Кислова Анна, ученица 11 «А» класса Свежевская Ольга Геннадьевна, учитель математики, руководитель проекта Заинтересовавшись поисками универсальных методов решения математических задач, ученица решила более обстоятельно изучить и изложить один из таких способов – решение уравнений и неравенств так называемым «методом мажорант». Аня начала накапливать материал, пользуясь различными пособиями по алгебре и началам анализа, вариантами вступительных письменных экзаменов по математике различных ВУЗов. Когда вышло в свет пособие для подготовки и проведения письменного экзамена по алгебре за курс основной школы (под ред. С.Шестакова), то ученица и там обнаружила множество красивых задач, к которым применим исследуемый ею метод. По мере накопления материала научный руководитель Ольга Геннадьевна предоставляла девочке возможность на уроке рассказывать детям о своих находках. Выступление ученицы в роли учителя, безусловно, и самой ей помогло глубже изучить проблему, а задаваемые старшеклассниками вопросы заставляли её искать научно-обоснованные, но в то же время доступные школьникам приёмы изложения материала.Неоценимую помощь оказала Кислова Аня девятиклассникам, штудирующим в настоящее время сборники подготовительных задач к экзамену по алгебре за курс основной школы и ЕГЭ. И девятиклассники, и одиннадцатиклассники непременно встретят на любом экзамене задания повышенной сложности, решаемые методом мажорант.Есть в проекте и задачи самого автора.Поскольку нет предела совершенствованию, то накопление материалов по данной теме будет продолжено следующими поколениями учащихся, а Кисловой Анне мы выразим благодарность за её творческий общественно-полезный труд. Представляем на ваш суд её проект.

Перед вами обложка пособия, выпущенного издательством лицея №1571 СЗОУО г. Москвы

сконцентрировать в одном пособии задачи, решаемые методом мажорант;показать ученикам практически универсальный алгоритм решения многих задач этим методом;заинтересовать читателя решением нестандартных задач, стимулировать самостоятельный поиск и создание собственных задач подобного типа. пополнить библиотеку методических пособий в школьном кабинете математики;передать этот проект в школьное издательство для создания брошюры «метод мини-макс»;на базе данного проекта провести 2-3 факультативных занятия для наших старшеклассников, что будет немало способствовать повышению их уровня математического развития.

К 11 классу мы с одноклассниками решили сотни различных уравнений и неравенств. Исследуя различные способы их решения, я пришла к выводу, что наиболее красивым, наиболее универсальным способом поиска решений является именно этот метод. Очень возможно, что кто-то из вас и не слышал такое выражение, как «метод мажорант». На самом деле, вы встречались с этим методом, просто не знали, как он называется. Некоторые математики называют этот метод по-другому: «метод математической оценки», «метод mini-max». Это очень красивый метод, и ему непременно надо научить всех. Решить неравенство: РешениеОценим левую часть неравенства: 1. это неравенство верно при любых значениях , причём существуют значения , при которых достигаются и значение 0, и значение 1. это неравенство верно при любых значениях , причём существуют значения , при которых достигаются и значение 0, и значение 1. 3. это неравенство верно при любых допустимых значениях х. (Искать допустимые значения х не обязательно, вы в этом сейчас убедитесь). Теперь вчитаемся в условие. Сумма трёх неотрицательных чисел не может быть меньше нуля, а равна нулю тогда и только тогда , когда каждое слагаемое равно 0.

Здесь достаточно решить одно из уравнений системы и проверить, подходят ли полученные значения х для остальных уравнений. Выберу самое лёгкое для решения уравнение, а именно третье: Теперь проверим, являются ли найденные корни третьего уравнения корнями других уравнений системы. Проверим первое значение переменной : Значит, не является решением данной системы.

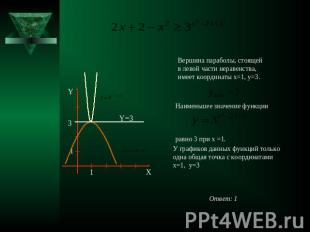
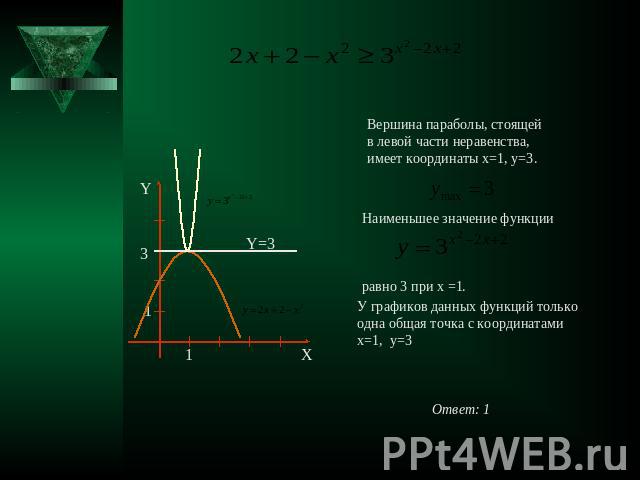
Вершина параболы, стоящей в левой части неравенства, имеет координаты x=1, y=3. Наименьшее значение функции равно 3 при x =1. У графиков данных функций толькоодна общая точка с координатамиx=1, y=3

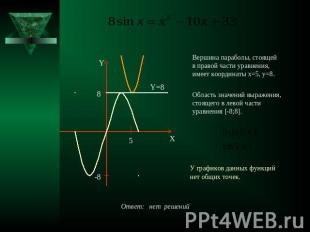
Вершина параболы, стоящейв правой части уравнения, имеет координаты x=5, y=8. Область значений выражения, стоящего в левой части уравнения [-8;8]. У графиков данных функцийнет общих точек.

Не удивляйтесь, что только на этих страницах, а не раньше, я решила изложить теоретические основы метода и снова затем продолжу решение задач. Теория станет более понятной, когда я с вами уже рассмотрела несколько примеров.В одном из пособий мы встречаем такое определение: «Мажорантой данной функции на множестве P называется такое число M, что либо для всех , либо для всех ». Мы знаем много мажорант для известных функций. Например, любое число, больше или равное 1, будет мажорантой для функций и на любом множестве.Основная идея метода мажорант состоит в следующем:Пусть мы имеем уравнение и существует такое число M, что для любого x из области определения и имеем: и , тогда уравнение эквивалентно системе:Естественно, у вас возникнет вопрос: «Как же искать такое число M?»

Существует несколько приёмов нахождения данного числа М.I способ связан с нахождением области значений заданных функций.ПримерРешить уравнение РешениеПроанализируем сначала правую часть уравнения. Рассмотрим квадратичную функцию , графиком которой будет являться парабола, ветви которой направлены вверх. Найдём координаты вершины данной параболы. Я думаю, что все знают, как это делается, поэтому не буду расписывать всё; координаты вершины (5;8).Тогда область значений этой квадратичной функции , причём значение 8 она принимает только один раз при х=5. В левой части уравнения находится функция . Область значение её [-8,8]. Значит, если графики этих функций имеют общую точку, то её ордината может быть только 8. Данное уравнение равносильно системе:Второе уравнение системы имеет единственный корень 5 , но при выполнении проверки первого уравнения получаем неверное равенство из чего делаем вывод, что система, а значит, и исходное уравнение, не имеет решений. Ответ: решений нет.

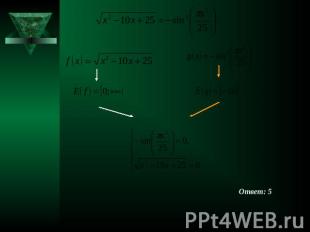
Решить уравнение Решение Проанализируем правую часть уравнения. Рассмотрим квадратичную функцию , графиком которой будет являться парабола, ветви которой направлены вверх. Найдём координаты вершины. Координаты вершины параболы (3;1). Значения этой квадратичной функции больше или равны 1, причём значение 1 функция принимает только один раз – при х=3. . Значения левой части данного уравнения не превосходят 1.Равенство между значениями данных функций может достигаться только тогда, когда обе части уравнения принимают значение 1. Следовательно, данное уравнение равносильно системе:Решив второе уравнение системы, получим .Проверяем, является ли число 3 корнем первого уравнения системы: равенство верное. Значит, значение 3 является решением исходного уравнения. Ответ: 3.

Рассмотрим теперь пример, содержащий логарифм. Решить неравенство РешениеНа первый взгляд, это не простой пример, но решается он не так уж сложно. Начинаем опять с анализа составляющих неравенства. Функция имеет наибольшее значение равное 1, причём достигается оно только при х=-4. Учитывая, что функция возрастает , и , делаем вывод о справедливости неравенства при любом значении х. Большим единицы произведение в левой части данного уравнения никак не может быть. Неравенство равносильно системе:Решаем первое уравнение системы:Проверяем является ли число (-4) корнем второго уравнения системы.Проверка: равенство верное Ответ: -4

Рассмотрим неравенство с тремя (!) переменными. РешениеНас выручит метод мажорант.Начнём с оценки левой части неравенства. Так как для любого действительного числа справедливо неравенство , а значение арифметического квадратного корня неотрицательно , то Следовательно, неравенство решений не имеет, так как

II способ. При поиске решения уравнений и неравенств часто бывает полезным применение базовых неравенств Неравенство Коши равенство достигается в этом неравенстве при a = b . Если же , то Оценка однородного тригонометрического многочлена Тригонометрические неравенстваОценка двух взаимообратных чисел , если равенство достигается при

Тогда значение дроби в правой части не больше 1 (меньше или равно 1) Значит, если данное уравнение имеет решения, то только тогда, когда обе части одновременно станут равными 1 при одних и тех же значениях переменных.ф

Решить систему уравнений: Смотрите – система уравнений с тремя (!) переменными. И тут снова на помощь приходит метод мажорант. РешениеРассмотрим первое уравнение системы как сумма двух взаимнообратных положительных чисел. Воспользуемся равенством для второго уравнения системы.

III cпособ. Нахождение мажоранты с помощью производной:ПримерНайти все решения уравнения лежащие на отрезке РешениеСначала запишем равносильное уравнение в удобном для нас виде: (*)Найдем наименьшее значение функции, стоящей в левой части уравнения, на отрезке .Отсюда видно, что f(x) возрастает на отрезках и , а убывает на отрезке . Значит, наименьшее значение функция f(x) принимает либо в точке , либо в точке .Но и , наименьшим значением функции f на данном отрезке оказалось значение 1. Итак, левая часть уравнения (*) не меньше 1 на отрезке , причем значение 1 может достигаться только при . А значение выражения в правой части уравнения (*) не больше 1. Значит, если значения функций совпадут, то этим значением может быть только 1. Проверкой убеждаемся, что и правая часть при х=1/2 принимает значение 1 . Ответ: 0,5

Дорогие девятиклассники! Для вас я решу несколько типичных заданий повышенной сложности из Сборника задач для подготовки и проведения экзамена по алгебре за курс основной школы (под редакцией С.Шестакова). Такие же задания ждут вас на предстоящем ЕГЭ (Едином государственным экзамене). И снова нас выручит метод мажорант. Решение Поскольку дискриминант каждого квадратного трёхчлена, стоящего под знаком арифметического квадратного корня, отрицателен, то при любых значениях переменной Х они принимают только положительные значения (коэффициент при Х2 положителен) Сумма неотрицательного числа (х-2)2 и числа 1 не меньше 1, а сумма неотрицательного числа и числа 5 не меньше 5. Тогда Причём знак равенства можно будет ставить только в случае, если Х=2, в остальных случаях сумма дробей в левой части уравнения окажется меньше числа 7/5, а нам этого не нужно. Математики говорят, что дробь 7/5 является мажорантой для функции

Мне показался интересным пример Значения первого арифметического квадратного корня больше или равны 1, причём равно 1 только в случае, если верно равенство . Аналогично, значения второго арифметического квадратного корня не меньше 5 (больше или равны 5).Следовательно, согласно методу мажорант, или методу «мини-макс», как его ещё называют, левая часть уравнения имеет минимум, равный 6, а правая часть представляет собой постоянную функцию со значением 6.Но чтобы значения функций совпали, надо проверить, имеет ли решение система: х-2у+1=0, 3х-у-2=0. Единственное решение этой системы (1;1) Ответ: (1;1) На первый взгляд, следующее неравенство сложно уже хотя бы тем, что оно с двумя переменными. Но метод «мини-макс», или метод мажорант и здесь нас выручит. РешениеЧисло 2 – наименьшее значение выражения, стоящего в левой части неравенства, причём достигается оно лишь при х = -2.Число 2 – наибольшее значение дроби, стоящей в правой части неравенства, причём достигается оно лишь при у=3.Левая часть неравенства никогда не станет меньше 2.Согласно применяемому нами методу остаётся единственная возможность, чтобы обе части неравенства приняли значение 2. Ответ: (-2;3)

Рассмотрим задание 4.3 D10.Решить неравенство, зная, что значения Х и У – целые числа. РешениеПо условию, Х и У целые числа, а тогда значения подкоренных выражений окажутся тоже целыми числами. Нельзя допустить, чтобы значения подкоренных выражений оказались больше или равны 1 (тогда неравенство не будет выполнено). Значит, нам ничего не остаётся, как потребовать, чтобы значения подкоренных выражений, будучи целыми в то же время были и меньше 1. Да это же целое число 0, и ничего другого!Составим и решим систему 3х-2у-4=0 2х+3у-7=0Эта система имеет единственное решение (2;1) Ответ: (2;1)

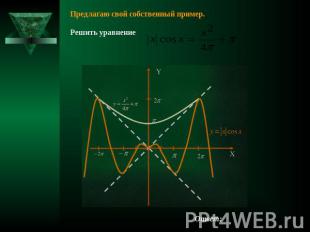
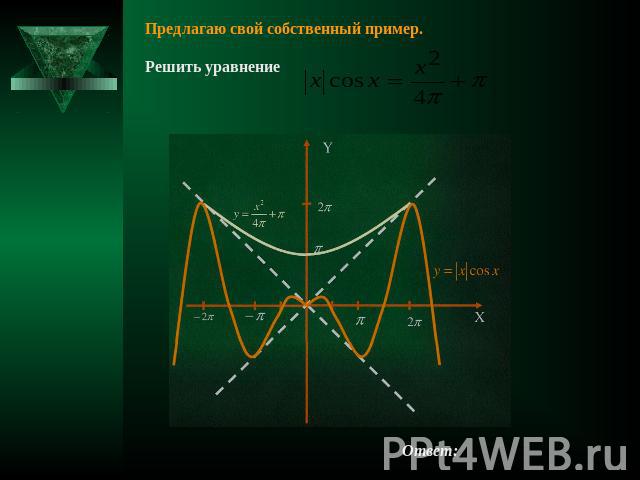
Предлагаю свой собственный пример. Решить уравнение

Задачи для самостоятельного решения:

Представленная нами работа будет очень полезна школьникам для подготовки к поступлению в ВУЗ.Работа будет полезна и студентам, потому что рассмотренный нами метод может быть с успехом применен и к решению многих задач по высшей математике;Подготовка старшеклассников к олимпиадам обязательно должна включать в себя и решение задач методом мажорант.