Презентация на тему: C1 метод мажорант

C1 метод мажорант

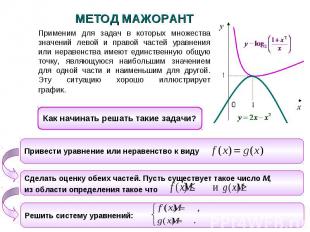
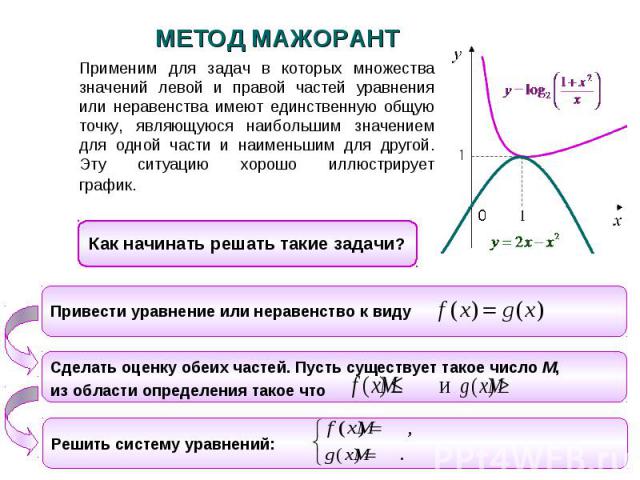
МЕТОД МАЖОРАНТ Применим для задач в которых множества значений левой и правой частей уравнения или неравенства имеют единственную общую точку, являющуюся наибольшим значением для одной части и наименьшим для другой. Эту ситуацию хорошо иллюстрирует график.       Как начинать решать такие задачи?Привести уравнение или неравенство к виду Сделать оценку обеих частей. Пусть существует такое число М, из области определения такое что Решить систему уравнений:

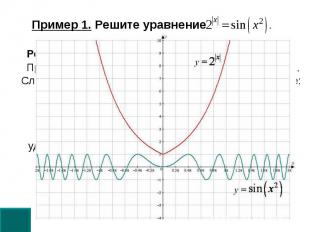
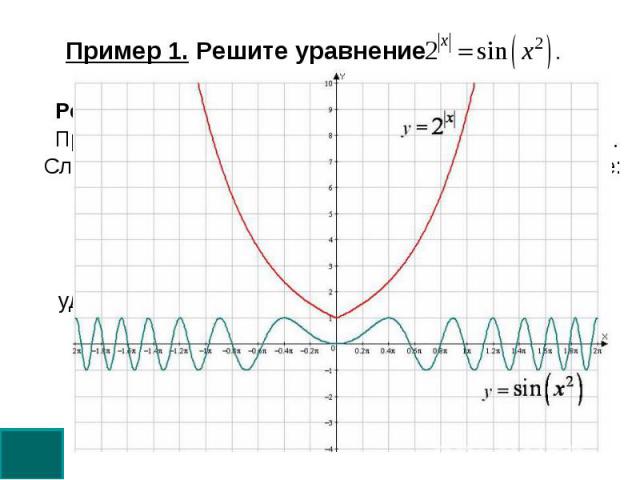
Пример 1. Решите уравнение

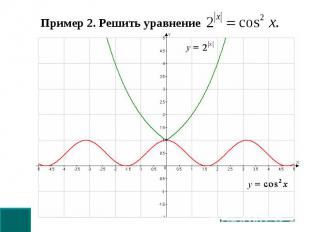
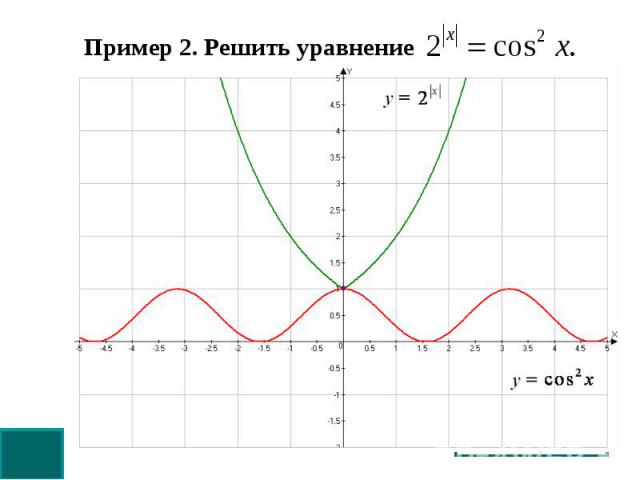
Пример 2. Решить уравнение

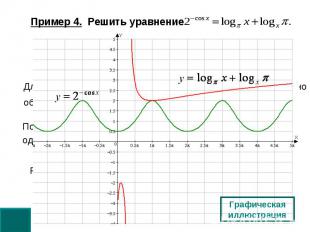
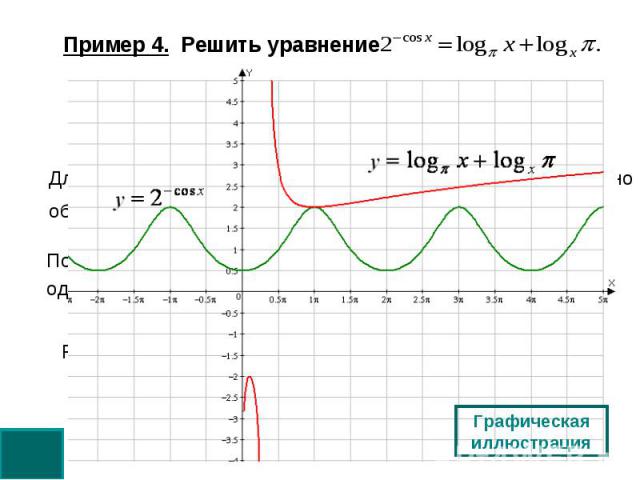
Пример 4. Решить уравнение

Пример 5. Решить уравнение Решение. Оценим обе части уравнения. выполняется тогда и только тогда, когда Решением первого уравнения системы являются значения При этих х найдем

Пример 6. Решить уравнение в том случае, когда оба слагаемых одновременно равны 1.Следовательно, данное уравнение равносильно системе уравненийрешая которые имеем

Пример 7. Решить уравнение Решение. Очевидно, что почленно эти неравенства, получаем:Следовательно, левая часть равна правой, лишь при условии: Значит, данное уравнение равносильно системе уравнений: Решая систему уравнений, получаем корни:

Пример 8. Решите уравнение Решение. Для решения уравнения Поэтому равенство возможно только при условииСначала решим второе уравнение: Корни этого уравнения Проверим справедливость первого равенства, подставив эти корни. При Итак, данное уравнение имеет единственный корень х = 0.

Пример 9. Найти все значения параметра а, при каждом из которых уравнение имеет решения. Найдите эти решения.Решение. Перепишем уравнение в виде При всех значениях х выражение При всех значения х выражения Следовательно, левая часть уравнения не меньше 4, а правая часть – не больше 4. Получаем систему: