Презентация на тему: Метод линейного сплайна

Метод линейного сплайна Выполнили работу ученицы 8 А классаМБОУ СОШ №7 им А.П. ГайдараАвдеева Юлия, Емельянова Светлана

Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным. Великий французский математик, физик, философ Блез Паскаль Цель: освоить метод линейного сплайна для построения графиков, содержащих модуль; научиться применять его в простых ситуациях.

Что такое сплайн? Под сплайном (от англ. spline — планка, рейка) обычно понимают кусочно-заданную функцию.Функции, подобные тем, что сейчас называют сплайнами, были известны математикам давно, начиная как минимум с Эйлера (4.04.1707-07.09.1783г.г.,швейцарский, немецкий и российский математик), но их интенсивное изучение началось, фактически, только в середине XX века. В 1946 году Исаак Шёнберг (21.04.1903- 21.02.1990г.г., румынский и американский математик) впервые употребил этот термин. После 1960 года с развитием вычислительной техники началось использование сплайнов в компьютерной графике и моделировании, что продолжается по сей день.

Содержание ВведениеОпределение линейного сплайнаОпределение модуляПостроение графиков Заключение

ВВЕДЕНИЕ Графики функций широко используются в различных областях инженерных знаний, поэтому умение строить, “читать”, прогнозировать их “поведение” имеют огромную роль в практической деятельности инженерных работников, метеорологов и людей других “математических” специальностей.

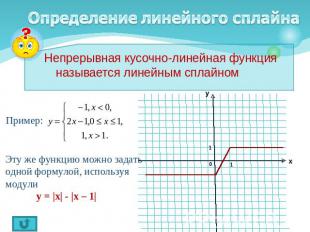
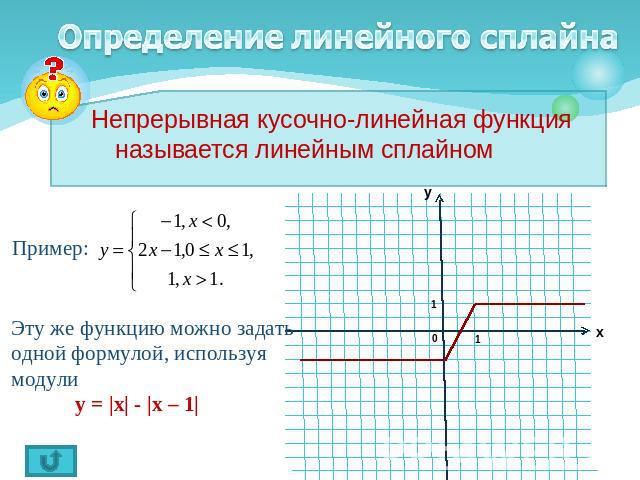
Определение линейного сплайна Непрерывная кусочно-линейная функция называется линейным сплайном Пример: Эту же функцию можно задать одной формулой, используя модули у = |x| - |x – 1|

Определение модуля Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово (омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках. Модулем числа а называется расстояние (в единичных отрезках) от начала координат до точки А (а). Это определение раскрывает геометрический смысл модуля. Модулем (абсолютной величиной) действительного числа а называется то самое число а ≥ 0, и противоположное число –а, если а<0.

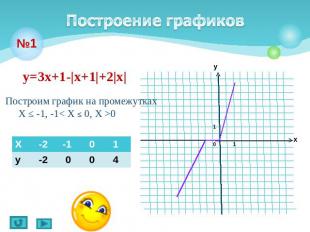
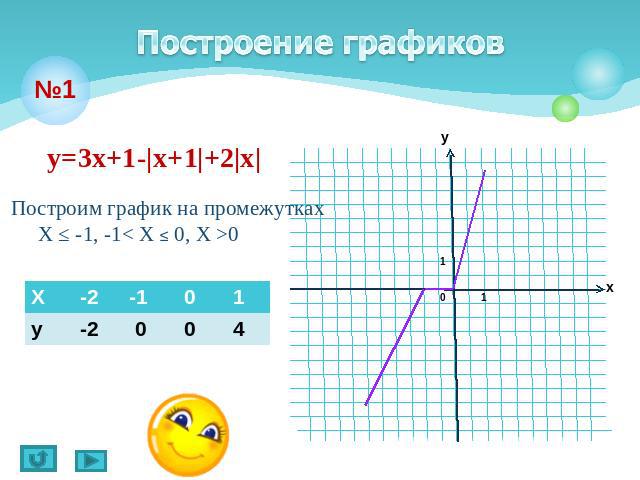
Построение графиков у=3х+1-|х+1|+2|х|Построим график на промежутках Х ≤ -1, -1< X ≤ 0, X >0

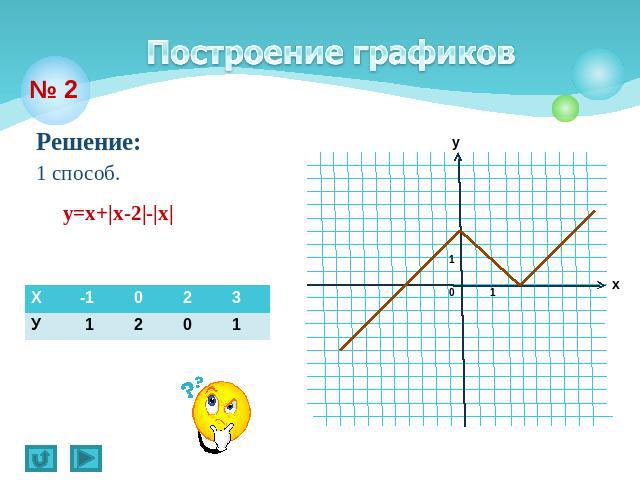
Решение:1 способ. y=х+|х-2|-|х|

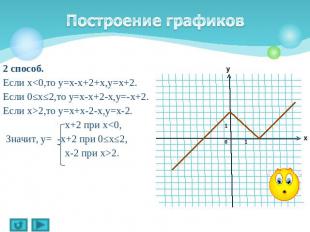
Построение графиков 2 способ.Если х<0,то у=х-х+2+х,у=х+2.Если 0≤х≤2,то у=х-х+2-х,у=-х+2.Если х>2,то у=х+х-2-х,у=х-2. х+2 при х<0, Значит, у= -х+2 при 0≤х≤2, х-2 при х>2.

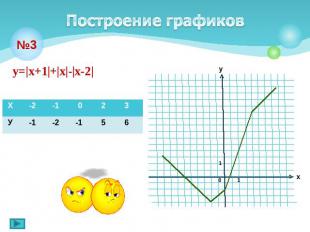
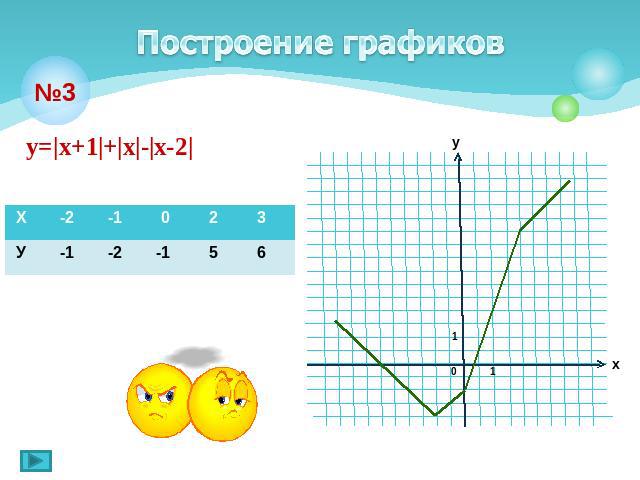
Построение графиков у=|х+1|+|х|-|х-2|

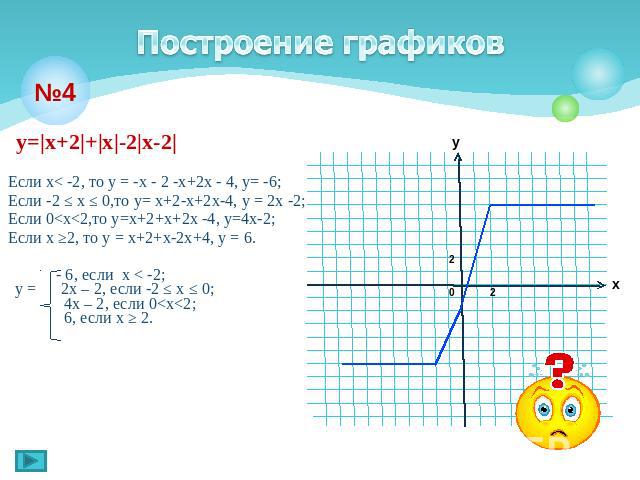
Построение графиков у=|х+2|+|х|-2|х-2| Если х< -2, то у = -х - 2 -х+2х - 4, у= -6; Если -2 ≤ х ≤ 0,то у= х+2-х+2х-4, у = 2х -2; Если 0<х<2,то у=х+2+x+2x -4, у=4х-2; Если х ≥2, то у = х+2+х-2х+4, у = 6. - 6, если х < -2;у = 2х – 2, если -2 ≤ х ≤ 0; 4х – 2, если 0<х<2; 6, если х ≥ 2.

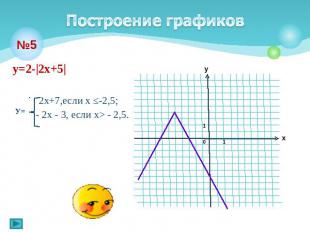
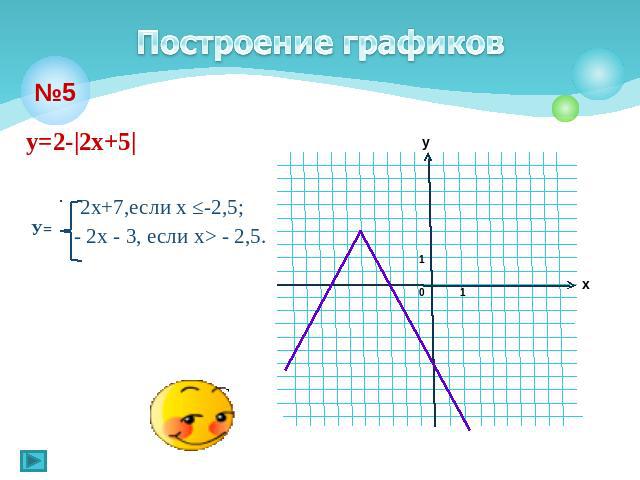
Построение графиков у=2-|2х+5| 2x+7,если х ≤-2,5; - 2х - 3, если х> - 2,5.

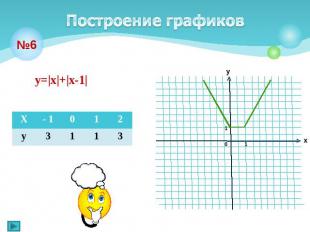
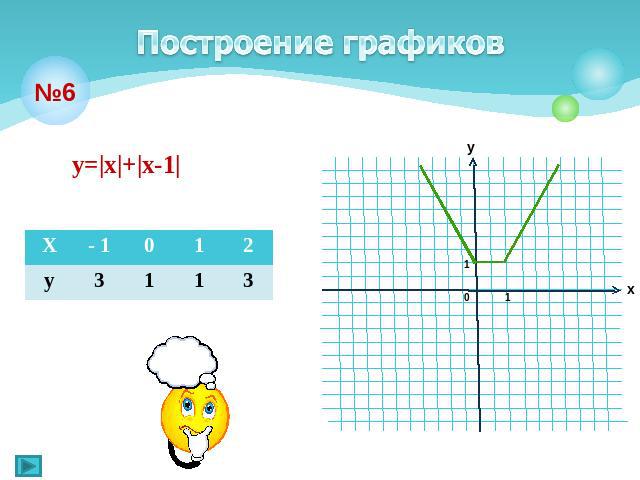
Построение графиков у=|х|+|х-1|

Мы узнали:Что называется линейным сплайном?Как строить графики, используя этот метод?Кем впервые был предложен этот метод?В каких областях науки и техники он нашел применение?

Козина М.Е. Математика. 8-9 классы: сборник элективных курсов. – Волгоград: Учитель, 2006.ВикипедиЯ свободная энциклопедия http://ru.wikipedia.org/wiki/Spline 3.Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 7 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение, 20094. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 8 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение, 2009Козина М.Е. Математика. 8-9 классы: сборник элективных курсов. – Волгоград: Учитель, 2006.ВикипедиЯ свободная энциклопедия http://ru.wikipedia.org/wiki/Spline 3.Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 7 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение, 20094. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Алгебра: учеб. Для 8 кл. общеобразоват. учреждений/ под ред. С. А. Теляковского. – 17-е изд. – М. : Просвещение, 2009