Презентация на тему: Кинематика криволинейного движения материальной точки

Кинематика криволинейного движения материальной точки Выполнила: ученица X класса «А»Катасонова НатальяПроверила: учитель физикиШевцова Э.Н.

Криволинейное движение Криволинейное движение тел, которые в данных условиях движения можно принять за материальные точки, часто встречается в повседневной жизни: поворачивают поезда и автомобили, велосипедисты и мотоциклисты на треке и т.д.

Пример 1. Самолёты в небе. Катасонова Н., МОУ Аннинский лицей

Пример 2. Движение по горному серпантину. Катасонова Н., МОУ Аннинский лицей

Пример 3. Аттракцион «Американские горки». Катасонова Н., МОУ Аннинский лицей

Пример 4. Аттракцион в аквапарке. Катасонова Н., МОУ Аннинский лицей

Пример 5. Движение по велотреку. Катасонова Н., МОУ Аннинский лицей

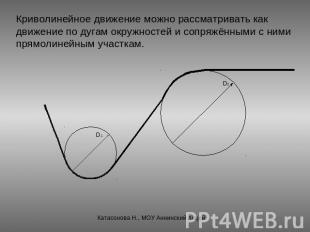
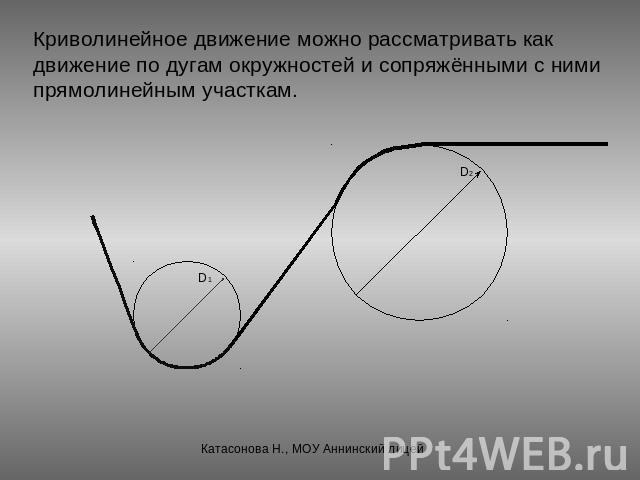
Криволинейное движение можно рассматривать как движение по дугам окружностей и сопряжёнными с ними прямолинейным участкам.

Не менее распространено движение по окружности. Скорость движения может оставаться постоянной по величине: практически с постоянной по модулю скоростью движутся Луна вокруг Земли и Земля вокруг Солнца. Нередки случаи, когда линейная скорость движения меняется. Например, когда колесо обозрения только начинает вращаться, скорость кабинок увеличивается, а когда заканчивает – скорость уменьшается. Прямолинейное движение можно рассматривать как движение по окружности бесконечно большого радиуса, что не может не наталкивать на мысль об описании движения по окружности с использованием метода аналогий.

Рисунок 1. Движение планет (модель Солнечной системы)

Рисунок 2. Движение электрона в планетарной модели атома

Рисунок 4. Карусель.

Рисунок 3. Работающие аттракционы.

Рисунок 5. Синхротрон Soleil, Париж.

Движение по окружности. Перемещение совпадает с хордой, поэтому средняя скорость направлена вдоль хорды: ( )

Вектор мгновенной скорости направлен по касательной к окружности в данной точке, т. к. хорда стягивается в точку.

При движении по окружности направление вектора скорости меняется при переходе из точки в точку; если модуль вектора скорости не меняется, то вектор изменения скорости направлен к центру окружности, поэтому тело движется с центростремительным ускорением.

Вывод формулы для расчёта центростремительного ускорения.

Угловое перемещение при движении по окружности. Движение по окружности можно характеризовать углом поворота радиус-вектора φ, называемого угловым перемещением. По аналогии с поступательным движением можно ввести понятие угловой скорости.

Описание вращательного движения. Линейная скорость. Угловая скорость. Т – период вращения; t – время; N – число оборотов. n – частота вращения. 1 радиан – угол, стягиваемый дугой, длина которой равна R. Катасонова Н., МОУ Аннинский лицей

Угловую скорость принято рассматривать как вектор, направленный вдоль оси вращения по правилу правого винта:Если винт вращать в направлении движения тела по окружности, то направление поступательного движения винта совпадёт с направлением вектора угловой скорости.

Связь линейной и угловой скоростей. При вращательном движении точек, лежащих на одном радиусе, угловая скорость не меняется, а линейная увеличивается по мере удаления точки от центра окружности. Центростремительное ускорение.

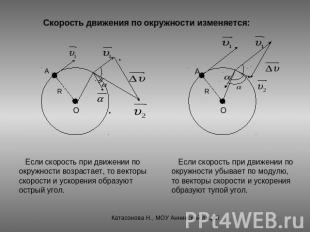
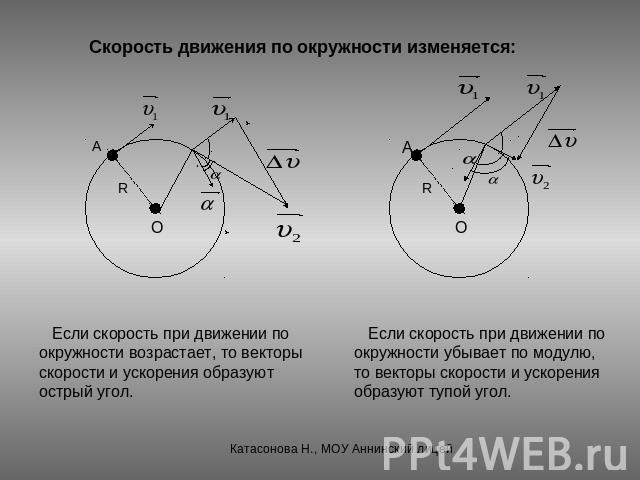
Скорость движения по окружности изменяется: Если скорость при движении по окружности возрастает, то векторы скорости и ускорения образуют острый угол. Если скорость при движении по окружности убывает по модулю,то векторы скорости и ускорения образуют тупой угол.

Вектор ускорения при прямолинейном движении может быть направлен к вектору скорости под любым углом в пределах от 0 до π. Его можно представить в виде двух составляющих: тангенциальной и нормальной.

Нормальное (центростремительное) ускорение ан характеризует изменение вектора линейной скорости по направлению и направлено перпендикулярно вектору скорости в сторону вогнутости траектории.Тангенциальное (линейное) ускорение ат характеризует изменение вектора линейной скорости по величине и направлено по касательной в данной точке траектории.Если за любые равные промежутки времени линейная скорость изменяется по величине одинаково, то величина тангенциального ускорения будет оставаться постоянной.

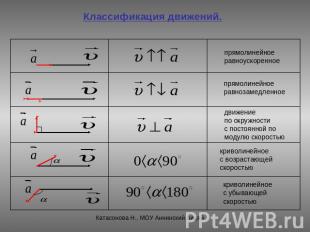
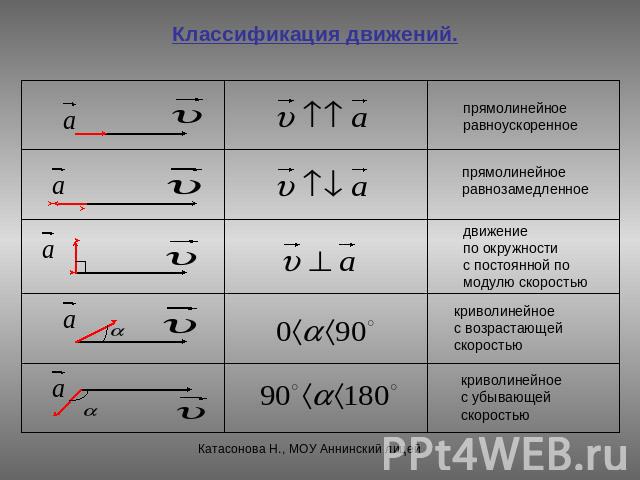
Классификация движений.

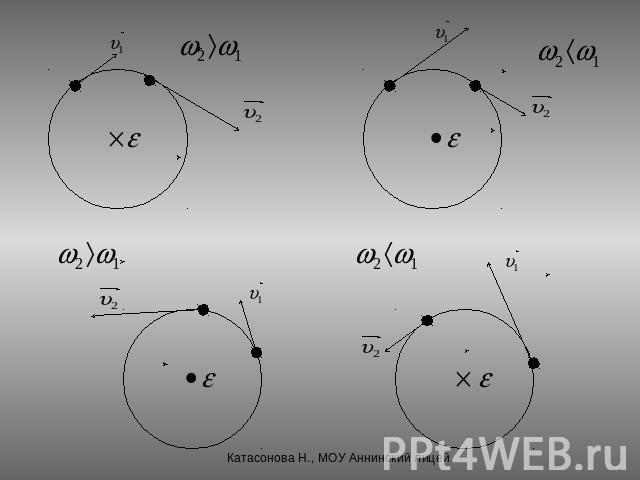
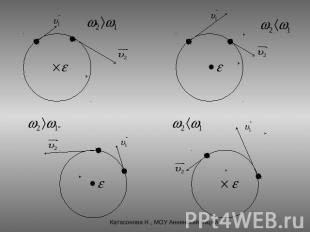
Угловое ускорение. Изменение угловой скорости можно по аналогии характеризовать угловым ускорением: Угловое ускорение - векторная физическая величина. Направление вектора углового ускорения определяется правилом буравчика с правой резьбой.Для определения направления вектора углового ускорения следует вращать буравчик по направлению движения тела по окружности. Вектор углового ускорения совпадает с направлением поступательного перемещения буравчика, если скорость возрастает и противоположен ему, если скорость убывает.

Сравнительная таблица

Вращательное движение твёрдых тел – тоже распространённый вид механического движения. Вращаются пропеллеры самолётов и гребные винты судов, лопасти гидротурбин и роторы электродвигателей, антенны радиолокаторов. Вращательное движение твёрдых тел можно описывать, используя аналогию с вращательным движением материальной точки.

Примеры вращательного движения твёрдых тел

Использованные информационные материалы Учебник для 10 класса с углублённым изучением физики под редакцией А. А. Пинского, О. Ф. Кабардина. М. : «Просвещение», 2005.Факультативный курс физики. О. Ф. Кабардин, В. А. Орлов, А. В. Пономарева. М. : «Просвещение», 1977 г. Трофимова Т. И. Курс физики: Учеб. пособие для вузов. М.: Высшая школа, 1990.Интернет