Презентация на тему: Прямая и обратная задачи кинематики криволинейного движения

Лекция 3

Прямая задача кинематики криволинейного движения. Критерии: угол поворота, угловая скорость, угловое ускорение. Прямая задача кинематики криволинейного движения. Критерии: угол поворота, угловая скорость, угловое ускорение. Обратная задача кинематики криволинейного движения – определение параметров движения.

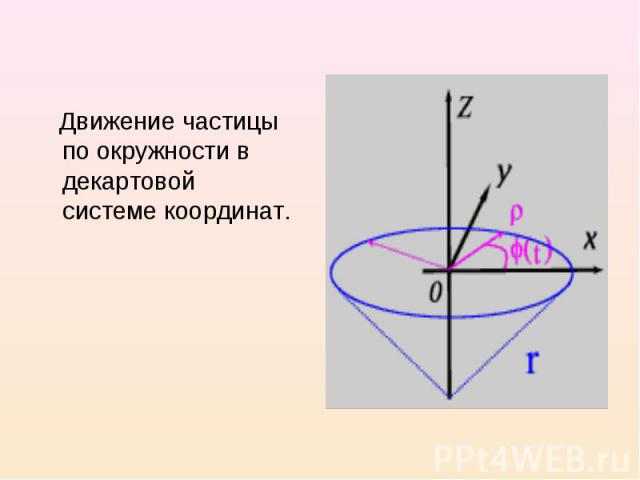
Движение по окружности и его кинематические характеристики.  Описание движения по окружности. Для начала рассмотрим один из простых случаев криволинейного движения частицы - движение, при котором меняется только направление ее радиус-вектора r(t). Уравнение, характеризующее изменение положения частицы со временем, будет иметь вид: r(t) = r·er(t), где r = const.     В декартовой системе координат уравнения движения примут вид: x(t) = ·cos (t);  y(t) = ·sin (t).     В случае равномерного движения по окружности угол изменяется со временем по закону (t) =  ·t +  0

Движение частицы по окружности в декартовой системе координат. Движение частицы по окружности в декартовой системе координат.

Угловые кинематические характеристики.  Рассмотрим движение частицы в плоскости XY в полярных координатах: = const, = (t).     При таком движении она обладает одной степенью свободы. Движение такой частицы удобно характеризовать величиной углового перемещения: = (t + t) - (t).

Вектор угловой скорости и ускорения. То, что величина элементарного углового перемещения действительно является вектором, можно доказать, выразив ее как комбинацию других известных нам векторных величин. Докажем это на примере вектора угловой скорости , который параллелен d .  Используя определение угловой скорости как производной от угла по времени: = d /dt     уравнение для нахождения угловой скорости, как комбинации известных нам векторов v и : = [ ·v]/ 2.    

Вектор углового ускорения  вводится по аналогии с поступательным движением, т.е. как производная от угловой скорости по времени: Вектор углового ускорения  вводится по аналогии с поступательным движением, т.е. как производная от угловой скорости по времени: = d /dt.     Вектор углового ускорения в случае движения частицы при неизменной ориентации ее оси вращения в пространстве сонаправлен этой оси (направлен по или против вектора ).  В случае произвольного движения частицы вокруг неподвижного центра в трехмерном пространстве направление оси вращения, а, следовательно, и вектора может изменяться. Вектор угловой скорости в любой момент времени при этом будет иметь три независимых компонента: = { x, y, z}.

Криволинейное движение. Нормальное и тангенциальное ускорения. Нормальное ускорение. Поскольку вектор ускорения при криволинейном движении сориентирован по отношению к скорости под произвольным углом, то разложим его на нормальную и тангенциальную составляющие: a = an + a = an·n + a · .    an = d /dt = 2/R   Нормальное ускорение характеризует изменение скорости по направлению. Вектор нормального ускорения равен an = 2/R·n.

Тангенциальное ускорение. Тангенциальное ускорение характеризует изменение скорости по величине. Вектор тангенциального ускорения равен: a = d /dt· .     Сам вектор полного ускорения состоит из суммы двух слагаемых: a = d( · )/dt = d /dt· + ·d /dt.     Первое слагаемое представляет собой его тангенциальную составляющую, а второе - нормальную составляющую, причем d /dt = /R·n.