Презентация на тему: Элементы комбинаторики и теории вероятностей

Элементы комбинаторики и теории вероятностей Андреева Алина Ивановна ГОБУ гимназия 293 Г. Санкт Петербург

Цель урока: Устранить пробелы в знаниях, повторить , обобщить и систематизировать знания, умения и навыки, необходимые для нахождения вероятности событий при решении задач на ЕГЭ Развитие умений сравнивать, обобщать, находить различные способы решения задач. Воспитание умение ставить цели и реализовывать их.

План работы Постановка цели. Повторение изученного материала. Проверка домашнего задания. Закрепление материала. Проверка знаний. Итог. Домашнее задание.

Алгоритм нахождения вероятности 1.Определить, что является элементарным событием А. 2.Найти общее число элементарных событий N. 3.Определить, какие элементарные события благоприятствуют событию А, и найти их число N(A). 4.Найти вероятность Р(А) события А

Р В случайном эксперименте симметричную монету бросают сто раз. Найдите вероятность того, что решка выпадет при 101 бросании.

ОО РР ОР РО В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что решка выпадет ровно один раз.

РО РР ОО ОР Монету бросают трижды. Найдите вероятность того, что первые два броска оканчиваются одинаково.

В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно один раз ООО ООР ОРО ОРР РОО РОР РРО РРР

В случайном эксперименте симметричную монету бросают четырежды. Найдите вероятность того, что орёл не выпадет ни разу РРРР ООРР ОООР РРОО ООРО РРРО ОРРО ОРОО РРОР РООР РООО РОРР ОРОР ОРРР РОРО ОООО

2 способ Переформулируем вопрос: найти вероятность того, что решка выпадет 4 раза Вероятность выпадения решки при первом броске Т.к. бросков 4, то вероятность выпадения решки при каждом броске

На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 8 прыгунов из России и 9 прыгунов из Парагвая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что шестым будет выступать прыгун из Парагвая

Для Орлова возможны 25 партнеров, из них 9 русские Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участвуют из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России.

Будем считать, что первый француз уже занял место в какой-то подгруппе. В каждой подгруппе 17 человек. Вероятность того, что второй француз попадёт в ту же группу, что и первый, равна В группе иностранных туристов 51 человек, среди них 2 француза. Для посещения маленького музея группу случайным образом делят на 3 подгруппы, одинаковые по численности. Найдите вероятность того, что французы окажутся в одной подгруппе.

В первом случае 1000 - вся выборка, 5 неисправных среди всех 1000 садовых насосов; а во втором вся выборка 103, из нее 100 качественные В среднем из 1000 садовых насосов, поступивших в продажу, 5 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает. Фабрика выпускает сумки. В среднем на 100 качественных сумок приходится 3 сумки со скрытыми дефектами. Найдите вероятность того, что случайно выбранная в магазине сумка окажется качественной.

Ве ро ят ность того, что ко ман да Рос сии ока жет ся во вто рой груп пе, равна от но ше нию ко ли че ства кар то чек с но ме ром 2, к об ще му числу кар то чек. В чем пи о на те мира участ ву ют 16 ко манд. С по мо щью жре бия их нужно раз де лить на че ты ре груп пы по че ты ре ко ман ды в каж дой. В ящике впе ре меш ку лежат кар точ ки с но ме ра ми групп:  1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4.  Ка пи та ны ко манд тянут по одной кар точ ке. Ка ко ва ве ро ят ность того, что ко ман да Рос сии ока жет ся во вто рой груп пе?

Для по го ды на 4, 5 и 6 июля есть 4 ва ри ан та: ХХО, ХОО, ОХО, ООО (здесь Х — хо ро шая, О — от лич ная по го да). В Вол шеб ной стра не бы ва ет два типа по го ды: хо ро шая и от лич ная, причём по го да, уста но вив шись утром, дер жит ся не из мен ной весь день. Из вест но, что с ве ро ят но стью 0,8 по го да зав тра будет такой же, как и се год ня. Се год ня 3 июля, по го да в Вол шеб ной стра не хо ро шая. Най ди те ве ро ят ность того, что 6 июля в Вол шеб ной стра не будет от лич ная по го да. Най дем ве ро ят но сти на ступ ле ния такой по го ды:   P(XXO) = 0,8·0,8·0,2 = 0,128; P(XOO) = 0,8·0,2·0,8 = 0,128; P(OXO) = 0,2·0,2·0,2 = 0,008; P(OOO) = 0,2·0,8·0,8 = 0,128. Ука зан ные со бы тия не сов мест ные, ве ро ят ность их суммы равна сумме ве ро ят но стей этих со бы тий:  P(ХХО) + P(ХОО) + P(ОХО) + P(ООО) = 0,128 + 0,128 + 0,008 + 0,128 = 0,392.

Первый выиграет, если у второго выпадет 1, 2 или 3. Двое играют в кости - они по разу бросают игральный кубик. Выигрывает тот, у кого больше очков. Если выпадает поровну, то наступает ничья. Первый бросил кубик, и у него выпало 4 очка. Найдите вероятность того, что он выиграет.

Строки – результат первого броска, столбцы – второго В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 6 очков

Правила комбинаторики суммы произведения А или В А и В происходит хотя бы одно из событий происходят оба события Правила комбинаторики

вероятность того, что первый школьник станет обменивать чёрную ручку У двух школьников по четыре шариковых ручки (красная, зелёная, синяя и чёрная). Они наугад обменялись одной ручкой. Какова вероятность того, что у одного из них окажется две ручки чёрного цвета? - вероятность того, что второй школьник станет обменивать ручку другого цвета Т.к. по условию школьники не пронумерованы, то искомая вероятность Вероятность того, что обе чёрные ручки окажутся у второго школьника

Выбор формулы Учитывается ли порядок следования элементов? да нет сочетания перестановки размещения Все ли элементы входят в соединение? да нет

У Пети в кармане есть 8 монет, из которых 6 монет по рублю и 2 монеты по 10 рублей. Петя перекладывает какие-то три монеты в другой карман. Сколькими способами Петя может это сделать, если известно, что обе монеты по 10 рублей оказались в другом кармане? Из трёх монет две зафиксированы, выбираем из 8-2=6 монет 3-2=1 монету по рублю

В кармане у Пети было 4 монеты по рублю и 2 монеты по 2 рубля. Петя, не глядя, переложил какие-то три монеты в другой карман. Найдите вероятность того, что обе двухрублевые монеты лежат в одном кармане. Возможны 2 варианта: либо Петя двухрублёвые монеты вообще не перекладывал, либо переложил сразу обе. Если двухрублевые монеты не перекладывались, то 3 монеты по рублю можно выбрать из 4 способами. Если обе двухрублевые монеты переложены, то еще одну рублевую монету можно выбрать из 4 способами. Всего выбираем 3 монеты из 4+2=6 способами.

Чтобы пятирублевые монеты лежали в разных карманах, надо переложить только одну из них. Это можно сделать способами. Всего Петя переложил 3 монеты, придется переложить еще 2 монеты по 10 рублей. Таких монет у Пети 4, поэтому количество способов равно Переложить 3 монеты из 6 имеющихся можно способами.

1 2 3 4 5 6 123 124 125 126 134 135 136 145 146 156 234 235 236 245 246 256 345 346 356 456 2 способ

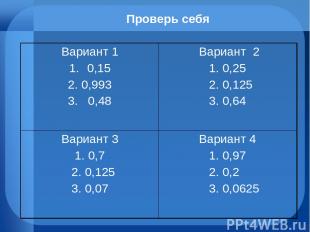
Проверь себя Вариант 1 0,15 2. 0,993 3. 0,48 Вариант 2 1. 0,25 2. 0,125 3. 0,64 Вариант 3 1. 0,7 2. 0,125 3. 0,07 Вариант 4 1. 0,97 2. 0,2 3. 0,0625

«Математика» 1 сентября №1 2012г И.Р. Высоцкий «В10 –вероятность» А.Л.Семенов, И.В.Ященко «ЕГЭ 2012. Типовые тестовые задания» А.Л. Семёнов, И.В.Ященко «ЕГЭ-2012. Математика. Типовые варианты. 30 вариантов» И.Р. Высоцкий, Ященко «ЕГЭ 2012. Математика. Задача В10. Рабочая тетрадь» Ф.Ф. Лысенко, С.Ю. Кулабухова «Математика. Элементы теории вероятностей и статистики. Подготовка к ЕГЭ-2012» http://alexlarin.net/ege/2012/turnir02122011.html http://www.berdov.com/ http://ege2012.mioo.ru/rf1112/ege111207m/index.htm http://mathege.ru/or/ege/Main Используемые ресурсы: http://reshuege.ru/