Презентация на тему: Делимость чисел 8 класс

Делимость чисел

Система упражнений по теме «Делимость чисел». Ее особенности: в действующих учебниках практически нет игр на отгадывание числа по каким-либо его свойствам. Поэтому эти задания будут интересны «математикам»; задания позволят узнать что-то новое о животных и растениях, о знаменитых людях и изобретениях, что вызовет интерес у «гуманитариев»; чтобы получить ответ, необходимо выполнить нетрадиционное математическое упражнение, что способствует развитию мышления.

Задача 1. Чтобы сохранить продукты питания на долгое время, люди замораживали, сушили или вялили их. Технологию консервирования предложил француз Николя Аппер. В каком году это произошло, если известно следующее: - число это четырехзначное, кратное 10; - первая и третья цифры его не являются ни простыми, ни составными числами; - вторая и третья цифры образуют число, кратное 9. Ответ: 1810.

Задача 2. В тот год англичанин Ричард Тревитик продемонстрировал одно из самых революционных изобретений в истории – первый паровоз. Правда , полноценным транспортным средством железная дорога стала лишь много лет спустя. Назовите год демонстрации, если известно следующее: - это четырехзначное число – произведение двух простых чисел; - первая цифра – ни простое, ни составное число; - сумма трех оставшихся цифр совпадает с наименьшим простым двузначным числом; - вторая цифра – наибольший общий делитель чисел 24 и 40; - все цифры этого года различны.

Решение . Первая цифра – 1, вторая – 8. Сумма трех последних цифр равна 11, сумма двух последних – 3. Этим свойством обладают числа 1812, 1821, 1803, 1830. Так как все цифры года различны, то остаются числа 1803 и 1830. Из них лишь 1803 – произведение двух простых чисел 601 и 3.

Ответ: 1803.

Задача 3. Это год рождения фотографии. Правда, на первом снимке мало, что можно было разглядеть, кроме размытых силуэтов, но это не обескуражило французского изобретателя Ж. Н. Ньепса. Назовите этот год, если известно следующее: - это четное четырехзначное число – произведение трех простых чисел, причем один из множителей – наименьшее двузначное простое число; - сумма же этих множителей – наименьшее общее кратное чисел 48 и 32.

Решение. Из первого условия узнаем два простых множителя – 2 и 11. Сумма трех множителей равна 96, то есть третий множитель – 83. Искомое число – 2*11*83 = 1826. Ответ: 1826.


Задача 4. Из всех живущих и вымерших животных самые большие глаза у гигантского кальмара, обитающего в Атлантике. Недавно была обнаружена особь, диаметр глаза которой составлял х мм. Найдите х, если известно, что это трехзначное число, сумма цифр которого есть квадрат простого числа, при этом последние две цифры совпадают, а первая цифра – квадрат четного числа.

Решение. Первая цифра – 4. Сумма цифр числа не превосходит 27 (число трехзначное) и может быть равно 4, 9, 25 (сумма – квадрат простого числа). Сумма двух последних цифр соответственно 0, 5, 21. Так как две последние цифры совпадают, то эта сумма – число четное, то есть 0. Ответ: 400.


Задача 5. На филиппинском острове Панай зоологи нашли новый вид млекопитающих – крупного грызуна из рода пышнохвостых крыс. От кончика носа до кончика хвоста крыса имеет длину более х см. Найдите х, если известно что это двузначное число. Если от этого числа отнять 3, то разность разделится на 3, а если отнять 4, то разность разделится на 4, если отнять 5, то разность разделится на 5.

Решение. Данное число кратно числам 3, 4, 5, поэтому оно равно 3*4*5*m. Так как число двузначное, а при m = 2 получаем трехзначное число, то искомое число – 60. Ответ: 60 см.


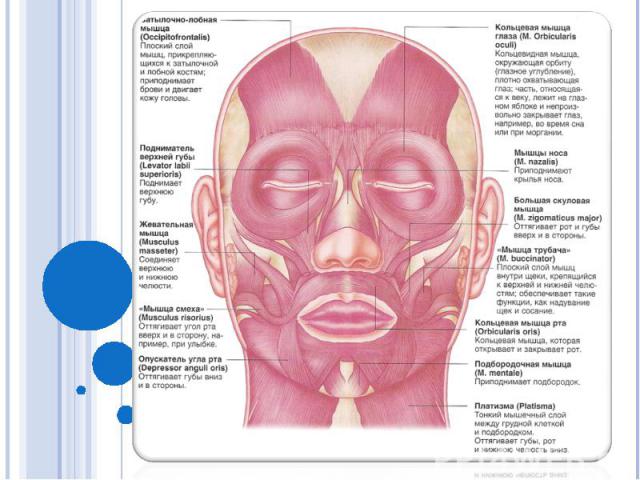
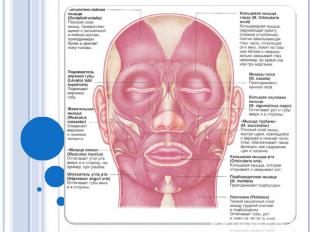
Задача 6. В улыбке участвуют x лицевых мышц, а для гримасы неудовольствия приходится напрягать у мышц. Найдите х и у, если известно, - что х – двузначное число, обладающее любопытным свойством: сумма его цифр не меняется при умножении на 2, 3, 4, 5, 6, 7, 8, 9, а его первая цифра не является ни простым, ни составным числом; - у – двузначное простое число, сумма цифр которого равна 7; если это число уменьшить на наименьшее простое число, то сумма цифр полученного простого числа уменьшится на столько же.

Решение. Первая цифра двузначного числа х равна 1. Перебором находим, что данным свойством обладает число 18. Так как сумма цифр двузначного простого числа у равна 7, то у не может превосходить 70 и может быть равен только 43 или 61. Если данные числа уменьшить на 2, то получим 41 и 59, сумма цифр первого числа меньше на 2. Ответ: х = 18, у = 43.

Задача 7. Наземные черепахи, вероятно живут дольше всех остальных известных животных. Они достигают возраста х лет, что возможно благодаря замедленному протеканию жизненных процессов. Найдите х, если известно, что: - сумма цифр этого трехзначного числа – простое число; - наибольший делитель, отличный от самого числа, - наименьшее трехзначное число; - число кратно 8.

Решение. Число кратно 100 и 8, то есть 200. Сумма цифр числа 200 – простое число. Числа вида 200m (m больше 1) имеют делитель больший 100, что противоречит второму условию. Ответ: 200.


Задача 8. Тапиры принадлежат к древнему семейству. Сегодня им грозит полное вымирание, так как они стали предметом охоты из-за своей прочной и высококачественной шкуры. Проживают тапиры на болотах или во влажных лесах от Венесуэлы до северной Аргентины. Они ведут ночной образ жизни, отличные пловцы. Тапир имеет сильные ноги и хоботообразную вытянутую верхнюю губу. Рост тапира не превышает х м при длине у м и весе z кг. Эти загадочные животные были открыты только в t году. Найдите x, y, z, t , если известно, что Х – не простое и не составное число; У – четное простое число; Z – наименьшее трехзначное число, кратное 75, две последние цифры которого совпадают; - среди делителей числа t есть два последовательных простых числа, а также число 101; первые две цифры числа t образуют число, являющееся наименьшим общим кратным 6 и 9.

Решение. Очевидно, x = 1, y = 2, z = 300. Единственные два последовательных простых числа – 2 и 3, поэтому t делится на 606. Первые его две цифры – 1 и 8, отсюда t = 1818. Ответ: x = 1, y = 2, z = 300, t = 1818.


Задача 9. Это единственный современный представитель голосемянных, появившихся 250 млн. лет назад. Японцы, китайцы и корейцы считают его священным деревом. В Германии его называют деревом Гете. Когда-то он написал одноименное стихотворение, в котором листья дерева выступают символом любви между двумя людьми. Название состоит из 6 букв. Числа, соответствующие буквам алфавита, удовлетворяют следующим условиям: - первое число совпадает с четвертым, это квадрат простого четного числа; - второе число – наибольший общий делитель чисел 50 и 60; - третье число – наименьшее общее кратное наименьшего простого нечетного числа и числа 5; - пятое число – наименьшее общее кратное чисел 4 и 6; - шестое число – сумма первого и пятого чисел.

Решение. Первое и четвертое числа равны 4, вторе равно НОД(50: 60) = 10, третье – НОК(3; 5) = 15, пятое – НОК(4; 6) = 12, шестое – 16. Ответ: гингко.


Задача 10. Из всех растений баобаб имеет самый толстый ствол. Оно растет в саваннах Центральной Африки. Свое название дерево получило в честь французского ботаника Мишеля Адансона, который описал его во время поездки по Сенегалу в х году. Баобаб отличается относительно низким, но очень толстым стволом, достигающим в диаметре у м, причем встречаются экземпляры с диаметром ствола до z м. найдите x, y z, если известно, что: - число х имеет только два делителя отличных от самого числа х и 1. Первый делитель – простое четное число. Второй – трехзначное простое число, причем первая цифра – квадрат второй цифры, две последние цифры образуют простое число; простым числом является и третья цифра; - число у – наименьшее общее кратное чисел 4 и 6; - число z – наименьшее общее кратное 5 и наименьшего простого двузначного числа.

Решение. х кратно 2. Ищем второй множитель. Так как первая цифра – квадрат второй цифры, то вторая цифра не превосходит 3. Остается проверить, какое число является простым из чисел 111, 113, 117, 423, 931, 937. Итак, х = 2 * 937 = 1874, у = НОК(4; 6) = 12, z = НОК(5; 11) = 55. Ответ: х = 1874, у = 12, z = 55.


Задача 11. Это дерево названо в честь вождя племени ирокезов, который создал письменность для своего народа. В переводе его имя означало «огромное дерево». Название самого растения состоит из 7 букв. Числа, соответствующие буквам алфавита, удовлетворяют следующим условиям: - первое число на единицу меньше наименьшего общего кратного 4 и 5; - у второго числа только два делителя, отличных от самого числа и 1, это два последовательных простых числа; - третье число на единицу меньше «чертовой дюжины»; - квадрат четвертого числа равен 9; - пятое – наименьшее двузначное число, в разложении которого только простые четные множители; - шестое число – наименьшее двузначное простое число; - седьмое число – наименьшее общее кратное четвертого и шестого чисел. Узнайте название растения.