Презентация на тему: По страницам знаменитой теоремы Пифагора

По страницам знаменитой теоремы Пифагора Выполнил ученик 10 «А»класса средней школы с.Яникой Габаев М. 2005 г

Теорема Пифагора Квадрат гипотенузы равен сумме квадратов катетов

Это прямоугольный треугольник

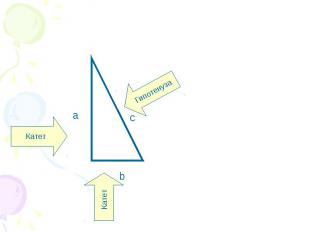
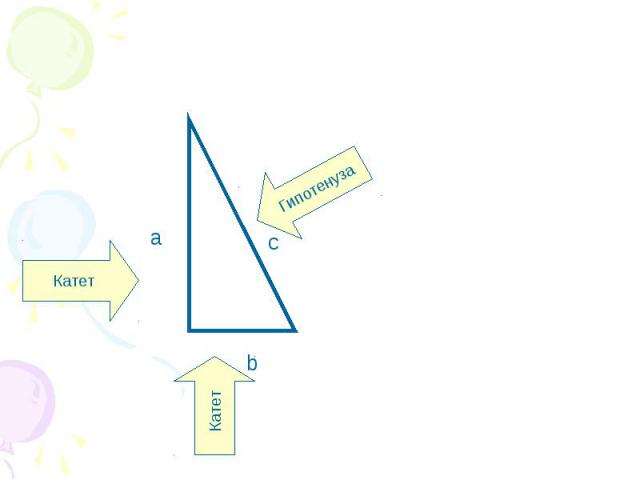
Гипотенуза Катет

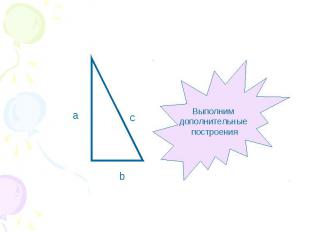
Выполним дополнительные построения

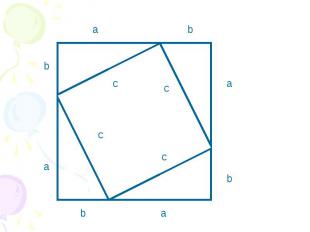
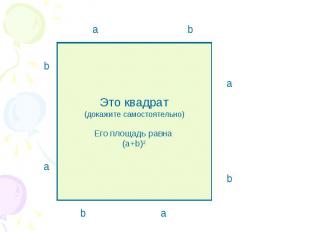
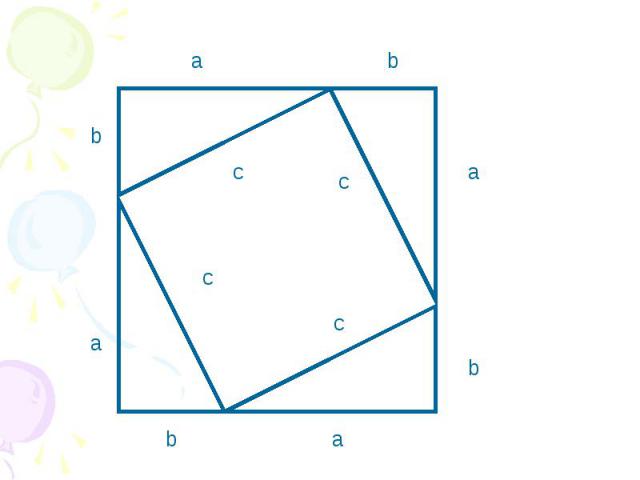
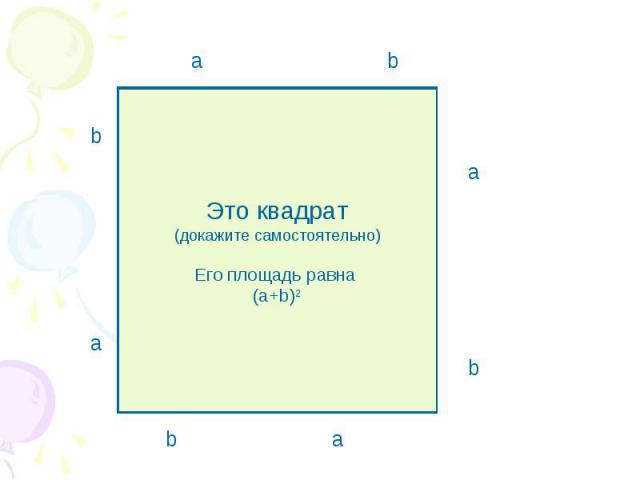
Это квадрат (докажите самостоятельно) Его площадь равна (а+b)2

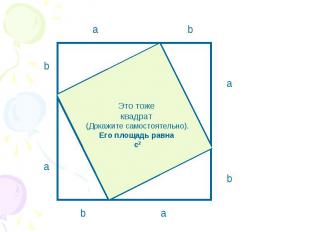
Это тоже квадрат (Докажите самостоятельно). Его площадь равна c2

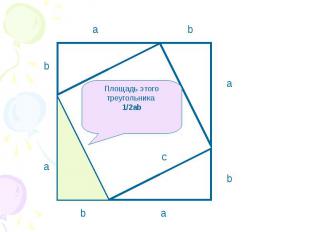
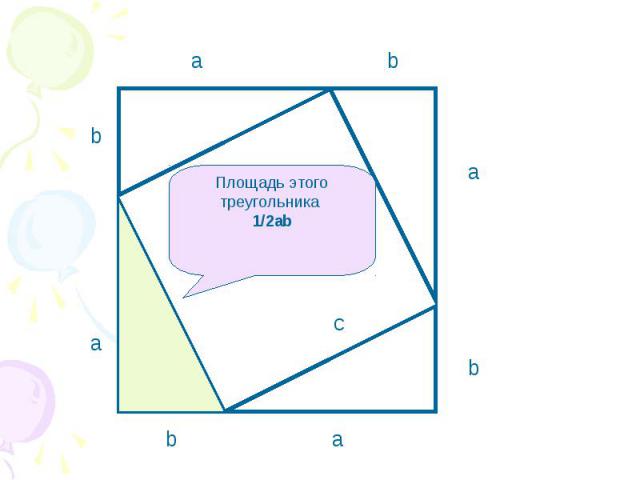
Площадь этого треугольника 1/2аb

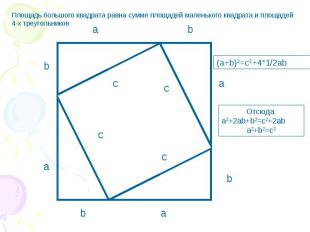
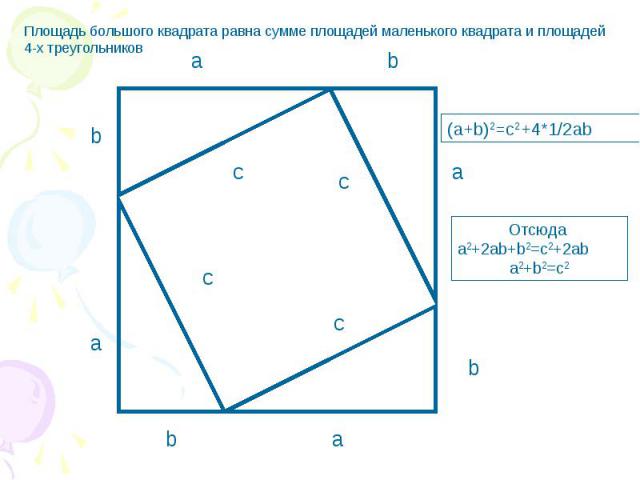
Площадь большого квадрата равна сумме площадей маленького квадрата и площадей 4-х треугольников (a+b)2=c2+4*1/2ab Отсюда a2+2ab+b2=c2+2ab a2+b2=c2

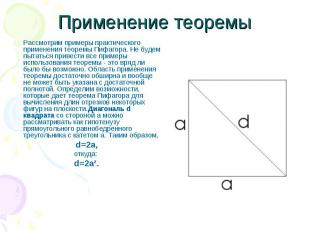
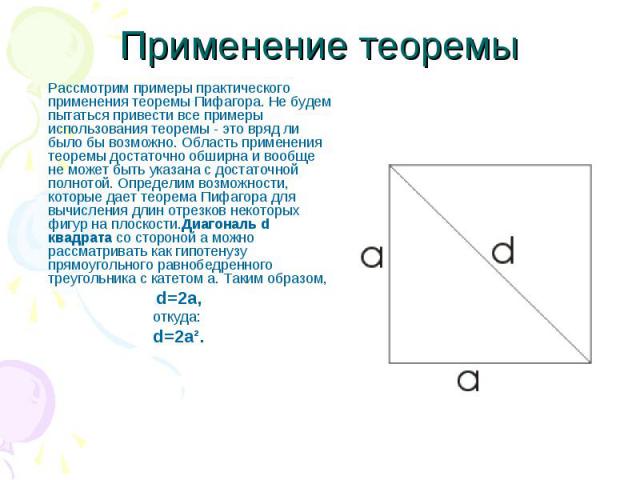
Применение теоремы Рассмотрим примеры практического применения теоремы Пифагора. Не будем пытаться привести все примеры использования теоремы - это вряд ли было бы возможно. Область применения теоремы достаточно обширна и вообще не может быть указана с достаточной полнотой. Определим возможности, которые дает теорема Пифагора для вычисления длин отрезков некоторых фигур на плоскости.Диагональ d квадрата со стороной а можно рассматривать как гипотенузу прямоугольного равнобедренного треугольника с катетом а. Таким образом, d=2a, откуда: d=2a².

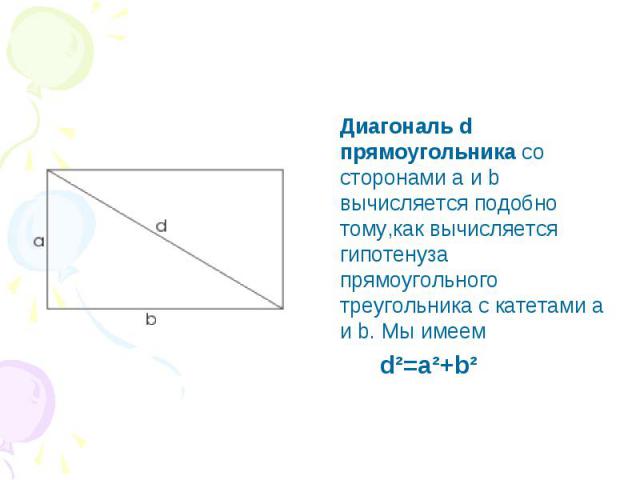
Диагональ d прямоугольника со сторонами а и b вычисляется подобно тому,как вычисляется гипотенуза прямоугольного треугольника с катетами a и b. Мы имеем d²=a²+b²

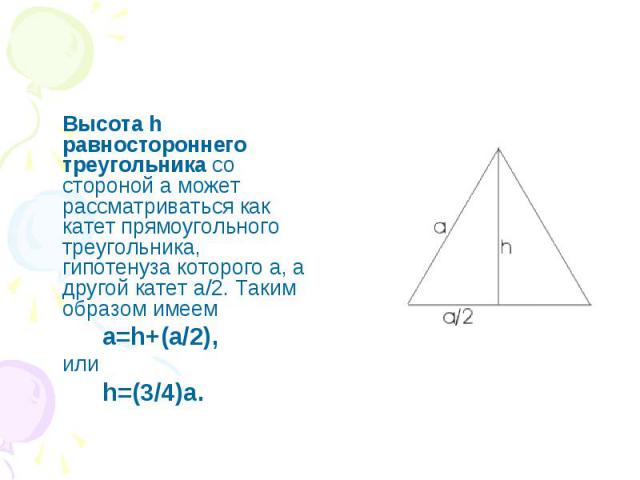
Высота h равностороннего треугольника со стороной а может рассматриваться как катет прямоугольного треугольника, гипотенуза которого а, а другой катет a/2. Таким образом имеем a=h+(a/2), или h=(3/4)a.

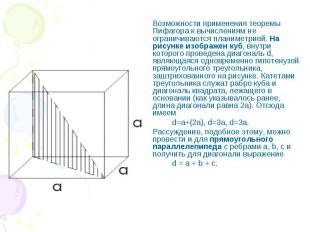
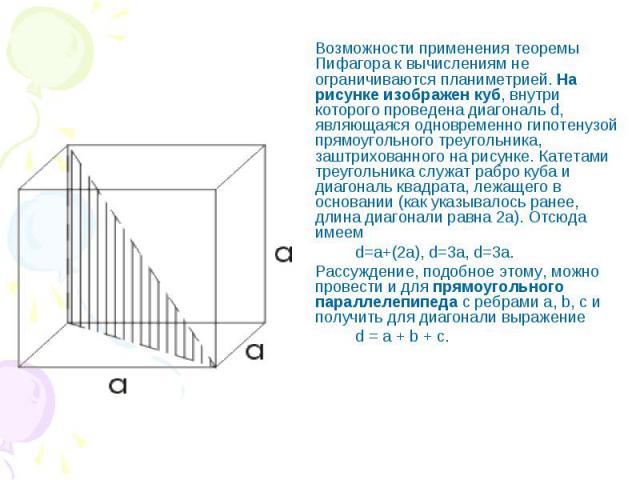
Возможности применения теоремы Пифагора к вычислениям не ограничиваются планиметрией. На рисунке изображен куб, внутри которого проведена диагональ d, являющаяся одновременно гипотенузой прямоугольного треугольника, заштрихованного на рисунке. Катетами треугольника служат рабро куба и диагональ квадрата, лежащего в основании (как указывалось ранее, длина диагонали равна 2а). Отсюда имеем d=a+(2a), d=3a, d=3a. Рассуждение, подобное этому, можно провести и для прямоугольного параллелепипеда с ребрами a, b, с и получить для диагонали выражение d = a + b + c.

В конце девятнадцатого века высказывались разнообразные предположения о существовании обитателей Марса подобных человеку, это явилось следствием открытий итальянского астронома Скиапарелли (открыл на Марсе каналы которые долгое время считались исскуственными) и др. Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно , было решено передать обитателям Марса сигнал в виде теоремы Пифагора. Неизвестно,как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.

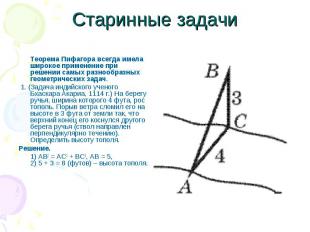
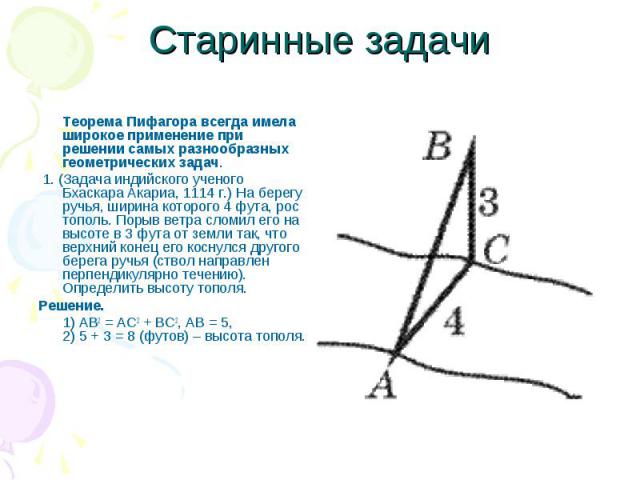
Старинные задачи Теорема Пифагора всегда имела широкое применение при решении самых разнообразных геометрических задач. 1. (Задача индийского ученого Бхаскара Акариа, 1114 г.) На берегу ручья, ширина которого 4 фута, рос тополь. Порыв ветра сломил его на высоте в 3 фута от земли так, что верхний конец его коснулся другого берега ручья (ствол направлен перпендикулярно течению). Определить высоту тополя. Решение. 1) AB2 = AC2 + BC2, AB = 5, 2) 5 + 3 = 8 (футов) – высота тополя.

Биография Пифагора Великий ученый Пифагор родился около 570 г. до н.э. на острове Самосе. Отцом Пифагора был Мнесарх, резчик по драгоценным камням. Имя же матери Пифагора неизвестно. По многим античным свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.Среди учителей юного Пифагора традиция называет имена старца Гермодаманта и Ферекида Сиросского (хотя и нет твердой уверенности в том, что именно Гермодамант и Ферекид были первыми учителями Пифагора). Целые дни проводил юный Пифагор у ног старца Гермодаманта, внимая мелодии кифары и гекзаметрам Гомера.

История теоремы Исторический обзор начнем с древнего Китая. Здесь особое внимание привлекает математическая книга Чу-пей. В этом сочинении так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5:"Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4".В этой же книге предложен рисунок, который совпадает с одним из чертежей индусской геометрии Басхары. Кантор (крупнейший немецкий историк математики) считает, что равенство 3 ² + 4 ² = 5² было известно уже египтянам еще около 2300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6619 Берлинского музея).

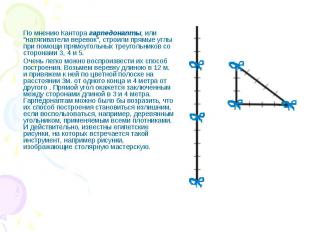
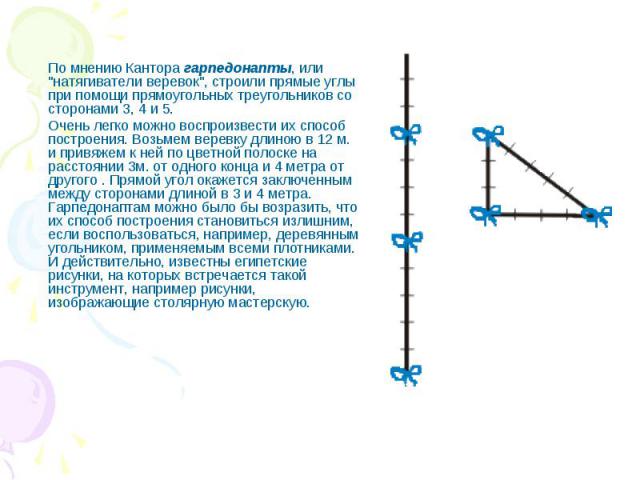
По мнению Кантора гарпедонапты, или "натягиватели веревок", строили прямые углы при помощи прямоугольных треугольников со сторонами 3, 4 и 5. Очень легко можно воспроизвести их способ построения. Возьмем веревку длиною в 12 м. и привяжем к ней по цветной полоске на расстоянии 3м. от одного конца и 4 метра от другого . Прямой угол окажется заключенным между сторонами длиной в 3 и 4 метра. Гарпедонаптам можно было бы возразить, что их способ построения становиться излишним, если воспользоваться, например, деревянным угольником, применяемым всеми плотниками. И действительно, известны египетские рисунки, на которых встречается такой инструмент, например рисунки, изображающие столярную мастерскую.

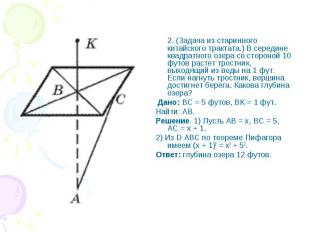
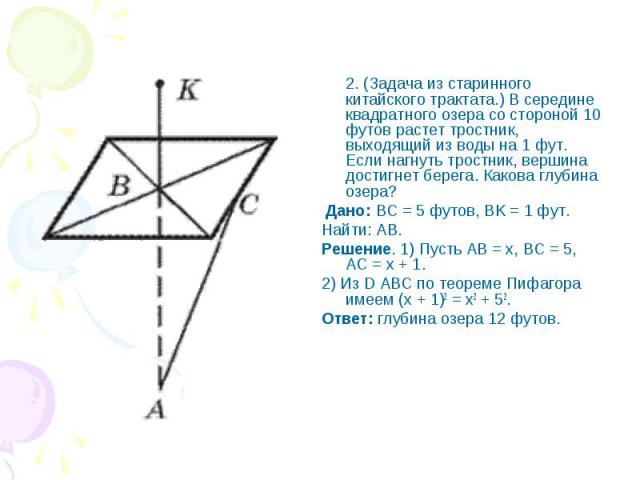
2. (Задача из старинного китайского трактата.) В середине квадратного озера со стороной 10 футов растет тростник, выходящий из воды на 1 фут. Если нагнуть тростник, вершина достигнет берега. Какова глубина озера? Дано: BC = 5 футов, BK = 1 фут. Найти: AB. Решение. 1) Пусть AB = x, BC = 5, AC = x + 1. 2) Из D ABC по теореме Пифагора имеем (x + 1)2 = x2 + 52. Ответ: глубина озера 12 футов.