Презентация на тему: Числа Фибоначчи

Высшее назначение математики … состоит в том, чтобы находить скрытый порядок в хаосе, который нас окружает.Винер Н.Числа ФибоначчиТПУ ИПР ТомсккАвтор: Константин ШелеповПреподаватель: Тарбокова Т.В.

Величайшим математиком Европы в средние века был Леонардо из Пизы, в современности он больше известен как Фибоначчи.Его отец был купцом, и Леонардо много путешествовал с ним. В путешествиях он получил те знания, которые помогли ему в дальнейшей работе.Леонардо Пизанский (Фибоначчи)Около 1170 — 1250 г.

От арабов Леонардо узнал о существовании индийской ныне «арабской» десятичной системы счисления с ее позиционными обозначениями и нулем.В своем известном труде «Книга об абаке» Фибоначчи показывает превосходство десятичной системы над римской.

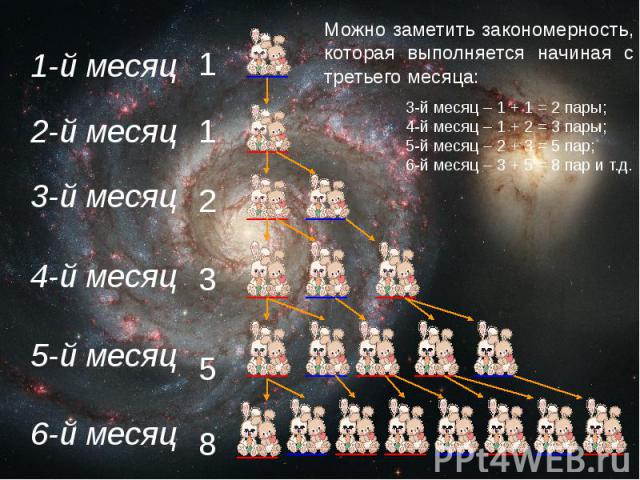
Задача про кроликов Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару, а рождают кролики со второго месяца после своего рождения.

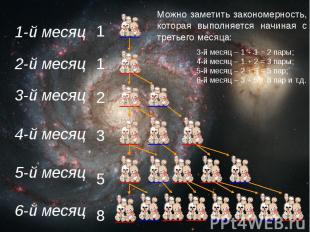
Можно заметить закономерность, которая выполняется начиная с третьего месяца:

Каждое следующее число равно сумме двух предыдущих.За 12 месяцев получится ряд чисел:1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144. Ответом задачи является число 144.Последовательность чисел получаемая в этой задаче названа в честь Леонардо: Числа Фибоначчи

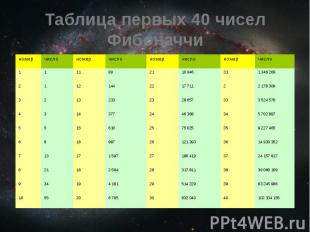
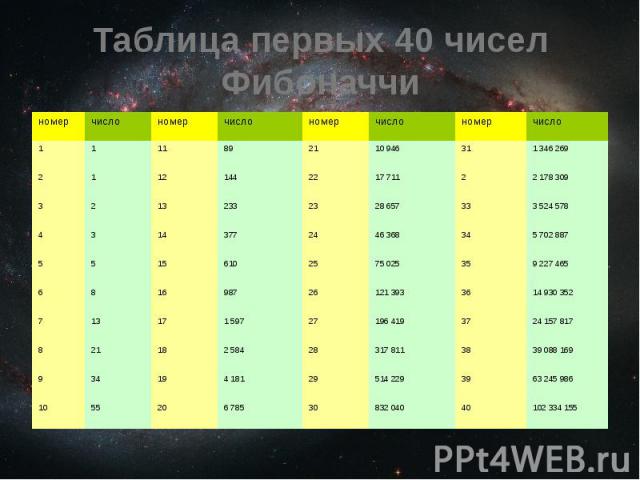
Таблица первых 40 чисел Фибоначчи

Числа Фибоначчи в древнем Египте Пирамида построена так, чтобы площадь каждой из ее граней была равна квадрату ее высоты. 238,7 : 147,6 = 1, 618Наблюдения показывают, что конструкция пирамиды основана на пропорции Ф=1,618.

Свойства чисел Фибоначчи Последовательность чисел обладает многими свойствами.Рассмотрим некоторые из них:Найдем отношение числа ряда Фибоначчи к последующему:Отношение каждого числа к последующему более и более стремится к числу ф = 0,618 по увеличении порядкового номера. Если найти отношения числа к предыдущему, то отношение каждого числа к предыдущему стремится к Ф =1,618 (обратному к 0,618).

Золотое сечение и числа Фибоначчи Золотым прямоугольником называют такой прямоугольник, у которого длина примерно в 1,6 раза больше ширины. Другими словами стороны прямоугольника образуют так называемое золотое сечение. Слово «сечение» обозначает «деление на части». Золотое сечение отрезка – деление непрерывной величины на две части в таком отношении, при котором меньшая часть так относится к большей, как большая ко всей величине.

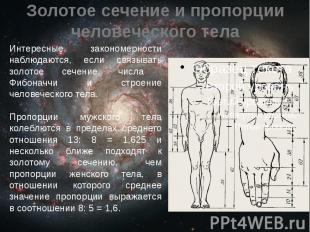
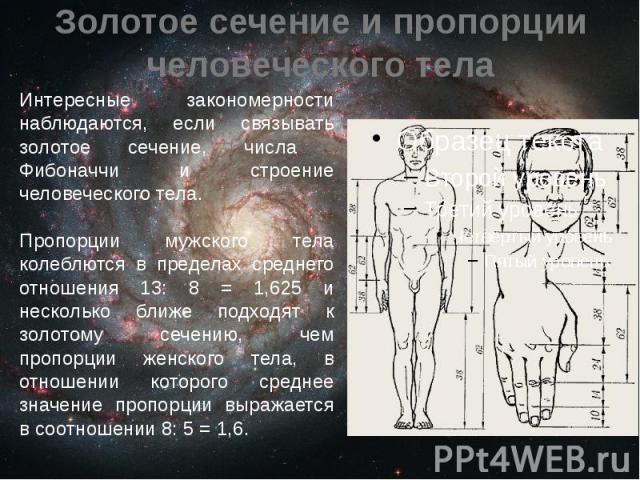
Золотое сечение и пропорции человеческого тела Интересные закономерности наблюдаются, если связывать золотое сечение, числа Фибоначчи и строение человеческого тела. Пропорции мужского тела колеблются в пределах среднего отношения 13: 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8: 5 = 1,6.

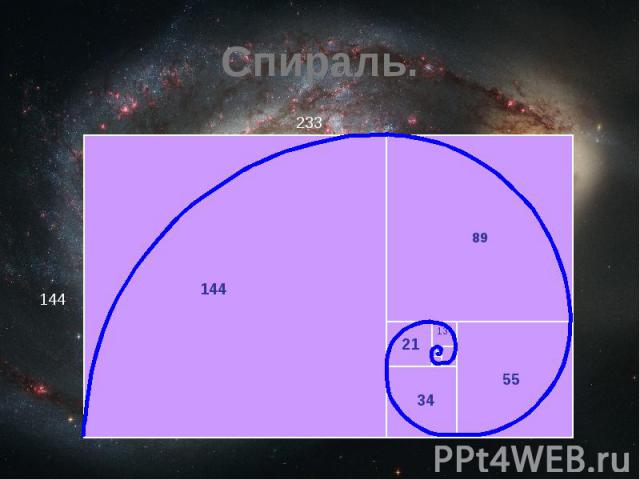
Спираль и числа Фибоначчи Гёте называл спираль «кривой жизни». Удивительно, что последовательность чисел Фибоначчи напрямую связана со спиральность в окружающем мире.

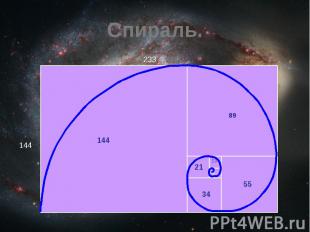
Спираль.

На многих шишках «чешуйки» расположены в трех спиралях, полого навивающихся на стержень шишки. Хорошо видны эти же спирали и на ананасах: обычно их бывает 8 и 13

Рассмотреть спираль так же можно в паутине или в том, как свернулась сороконожка .

Если посмотреть на многие кактусы сверху, то можно и здесь обнаружить ту же спираль, усики огурца или свернувшийся лист также демонстрируют спиралеобразное строение.

У многих сложноцветных (розы, маргаритки, ромашки) заметно, спиральное расположение отдельных цветков. Молодые побеги папоротника, закручены в спираль . Хорошо виден винтообразный рост веток дерева.

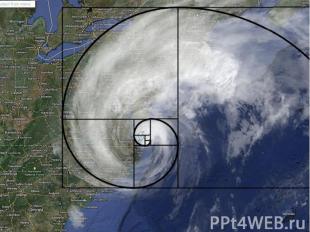
Можно увидеть спираль и в разных явлениях природы, например таких как: смерч, ураган, облака, морские волны. Наша галактика – это спираль.

Оказывается спираль Фибоначчи есть и на отпечатке пальца.

Даже ДНК человека это две свитые спирали. Винты и спирали действительно на каждом шагу окружают нас.

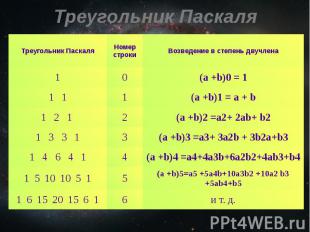
Треугольник Паскаля

Треугольник Паскаля

Парадокс с площадью

Можно заметить, что длины сторон фигур из данной задачи (2, 3, 5, 8, 13) являются последовательными числами Фибоначчи. Площади закрашенных фигур, разумеется, равны между собой (32 клетки), однако, то, что визуально наблюдается как треугольники 13×5, на самом деле таковым не является, и имеет разные площади (S13×5 = 32,5 клетки). То есть ошибка, замаскированная в условии задачи, состоит в том, что начальная фигура поименована треугольником (на самом деле это — вогнутый 4-угольник). Это отчётливо заметно на рисунках 1 и 2 — «гипотенузы» верхней и нижней фигур проходят через разные точки: (8,3) вверху и (5,2) — внизу. Секрет в свойствах синего и красного треугольников. Это легко проверить вычислениями.

Свойство чисел Фибоначчи, на котором основан парадокс с площадью

Некоторые свойства чисел Фибоначчи I свойство: Сумма n первых ряда Фибоначчи равна n+2 члену без единицы. a1 +a2+…an=an+2–1 II свойство: Сумма чисел Фибоначчи с нечётными номерами равна следующему числу с четным номеромa1+a3+a5+…+a2n-1=a2n

Некоторые свойства чисел Фибоначчи III свойство Сумма чисел Фибоначчи с чётными номерами равна следующему четному числу без единицы:a2+ a4+a6+ …+ a2n=a2n+1-1 IV свойство: Сумма квадратов первых n чисел Фибоначчи равна произведению n-го и следующего за ним члена.a12+ a22+a32+…+ an2= an•an+1

Спасибо за внимание