Презентация на тему: Использование Диофантовых уравнений при решении задач в математике и химии

Использование Диофантовых уравнений при решении задач в математике и химии

Цель: Рассмотреть использование неопределенных уравнений при решении задач в математике и химии

ДиофантАлександрийский-древнегреческий математик живший в IIIвеке.

х+ х +х+5+х+4 =х6 12 7 2 Ответ: 84 года

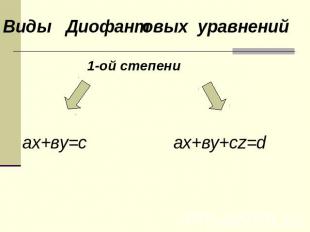
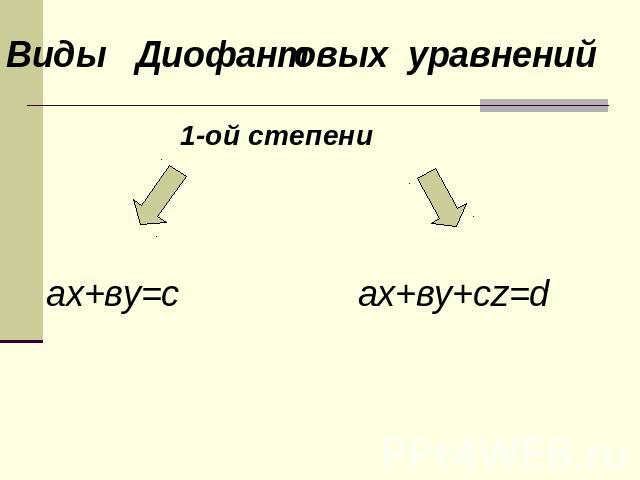
Виды Диофантовых уравнений 1-ой степени ах+ву=с ах+ву+сz=d

Однородное уравнение в целых числах В уравнении ах+ву=с, если с=0,то оно называется однородным уравнением и имеет вид ах+ву=0.Это уравнение имеет бесконечное множество решений в целых числах.

Теорема Если числа а и b- взаимно простые, то уравнение вида ах+bу=0 имеет бесконечно много решений в целых числах. Доказательство:Рассмотрим уравнение 80х+126у=0Разложим коэффициенты а = 80 и b=126 на простые множители: а = 2в4 * 5 и b= 2* 3в2*7. После сокращения на 2 мы получим уравнение40х+63у=0,(1) 40 и 63- взаимно простые числа Перепишем уравнение (1) в виде:2*5* х = -3во2 * 7*у. (2) у = 2в3*5*u= 40u ,(З) Х = 3в2* 7*v = 6Зv,(4) u=-v все пары (u; -u) вида (-n;n) уравнения (2) можно записать в виде: х =63n, у = -40n При n=1, (63;-40), при n=2,(126;-80) и т.д.

Однородное уравнение в целых числах в случае когда с ≠ 0 4х-6у=17Это уравнение не будет иметь решений т.к. 4 и 6- кратны 2, а 17 не кратно 24х-6у=18, 2х-3у=9, х = (9+3у)/2, выделим целую часть из полученной дроби и представим х в виде целой дробной части.Х=у+4+(у+1)/2 (у+1)/2- является целым числомПусть (у+1)/2=n, где n- целое.У=2n-1X=2n-1+4+(2n-1+1)/2X=3n+3 Ответ: х=3n+3;2n-1, где n€Z

Задача «Покупки» Отправляясь за покупками, я имел в кошельке около 15 рублейотдельными рублями и 20-ти копеечными монетами. Возвратившись, я принес столько отдельных рублей, сколько было у меня первоначально 20-ти копеечных монет, и столько 20-ти копеечных, сколько имел я раньше отдельных рублей. Всего же уцелела у меня в кошельке треть той суммы, с какой я отправлялся за покупками.Сколько стоили покупки?Х- первоначальное у- 20-ти копеечные монеты100х+20у было до похода в магазин100у+20х стало после похода в магазин 100х+20у=3(100у+20х) Ответ: 960 копеек

Задача по химии Даны два сплава железа и магния массой 100г и 80г соответственно. Известно, что в первом сплаве железа в два раза больше, чем во втором, а масса магния одинакова. Установите количественный состав сплавов. Решение: Пусть m(Fe)2=x => m(Fe)1=2x Mg=yПолучим уравнения 2х+у=100 (1) х+у=80(2) Выразим из 2-ого уравнения х и подставим в 1-ое уравнение. 2(80-у)+у=100 160-2у+у=100 160-у=100 160-100=у У=60 100-60=40 ( Fe1) 80-60=20 ( Fe2) Ответ: 40г.,.20г.

ВыводыУмения решать Диофантовы уравнения способствуют:-нахождению остроумных и простых решений;-развитию математических навыкови логического мышления;- быстрому и правильному решению задач по другим предметам.