Презентация на тему: MSC.Nastran 101 2006 - 5

Раздел 5 Верификация модели

Краткий обзор Типичные ошибки; сингулярности и механизмы Процедура автоматической проверки в MSC NASTRAN Диагностирование ошибок Основные виды проверок Практика моделирования Жесткие (RIGID) элементы и граничные условия, задаваемые уравнением (MPC) Симметрия

Типичные ошибки; сингулярности и механизмы

Сингулярности и механизмы Сингулярность обуславливается отсутствием жесткости или недостаточной жесткостью конструкции по какой-либо степени свободы. Матрица жесткости не может быть обращена, если она сингулярна Некоторые примеры сингулярности: Возможность движения модели как твердого тела Соединение элементов с различным числом степеней свободы Некорректная перекрестная связь степеней свободы

Сингулярности и механизмы (продолжение) Движение модели как твердого тела Граничные условия должны быть заданы таким образом, чтобы все 6 форм движения "твердого тела" были зафиксированы. Движение твердого тела Адекватные закрепления

Сингулярности и механизмы (продолжение) Движение модели как твердого тела Самая распространенная ошибка: не сшитые сетки (процедура ‘Equivalence’ в MSC Patran или аналог в любом другом препроцессоре). В этом случае сетки не связаны между собой – возникает сингулярность

Процедура автоматической проверки в MSC Nastran

AUTOSPC Если существуют очевидные сингулярности, MSC Nastran пытается исключить их автоматически Запись секции Bulk Data: PARAM,AUTOSPC,YES или в секции Case Control: AUTOSPC = Yes (указывает программе на необходимость автоматического приложения SPCs к этим сингулярностям) PARAM,AUTOSPC,YES применяется по умолчанию для большинства типов анализа.

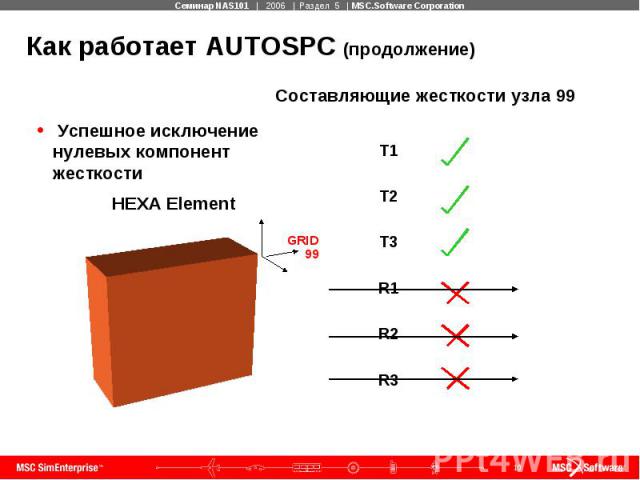
Как работает AUTOSPC

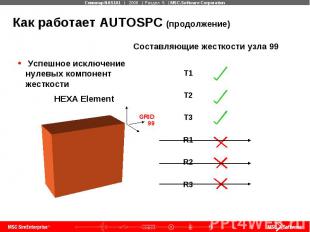
Как работает AUTOSPC (продолжение)

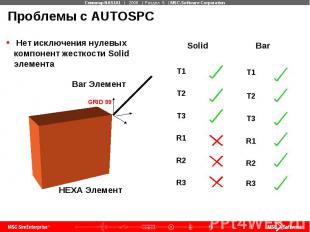
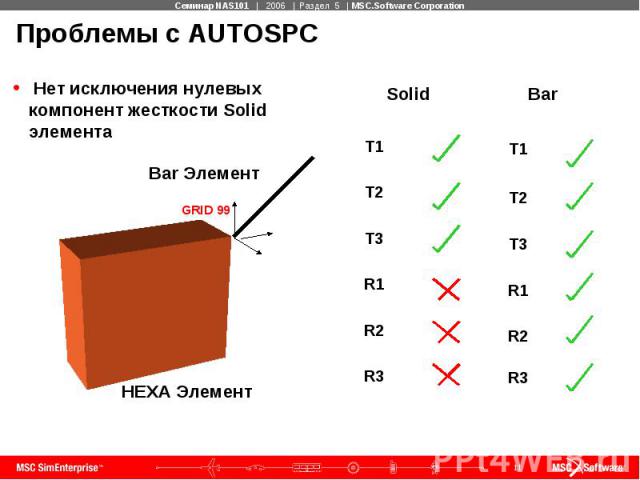
Проблемы с AUTOSPC

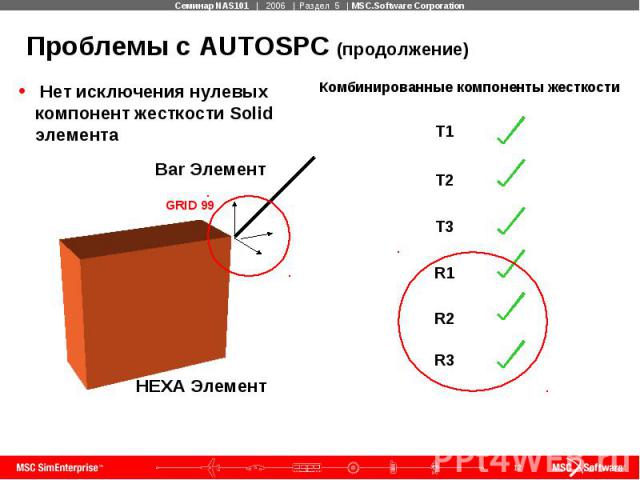
Проблемы с AUTOSPC (продолжение)

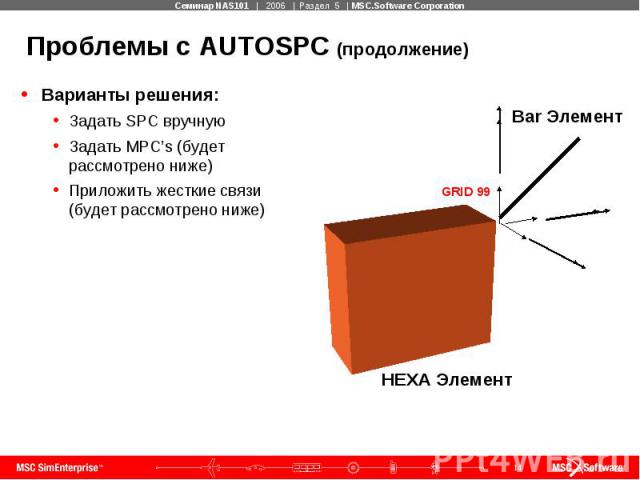
Проблемы с AUTOSPC (продолжение)

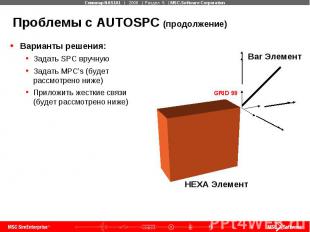
Проблемы с AUTOSPC (продолжение)

Распечатка AUTOSPC (продолжение) Что означает USET? Представим все степени свободы узлов и скалярных точек в конечноэлементной модели как члены одного набора перемещений (displacement set). Этот глобальный набор (Global set) называется g-set а соответствующий набор перемещений известен как Ug. [Kgg] должна быть несингулярной, чтобы уравнение можно было решить. Чтобы достичь отсутствия сингулярности матрицы, пользователь должен определить независимые поднаборы (subsets) набора {ug}, на которые он будет разделен в процессе приведения матрицы Например: um Степени свободы, исключаемые граничными условиями MPC us Степени свободы, исключаемые граничными условиями SPC Исключение М и S наборов (sets) даст набор F (free - свободный), который обычно и решается, чтобы получить неизвестные перемещения. Для более подробной информации о наборах перемещений смотри Приложение B – MSC Nastran Quick Reference Guide и MSC NASTRAN Linear Static Analysis Users’ Guide.

AUTOSPC

Проблемы с AUTOSPC (продолжение) Варианты решения: PARAM,K6ROT, 100 Это новое рекомендуемое значение по умолчанию PARAM,SNORM, 20 Рекомендуемое значение

Установки по умолчанию для SNORM и K6ROT в V2001 Оболочечные нормали обеспечивают более высокую точность PARAM, SNORM, 20. стоит по умолчанию в V2001 PARAM, K6ROT, 0. стоит по умолчанию для всех линейных последовательностей решений в V2001 Уменьшает размер рабочего файла, так как вращательная степень свободы в плоскости элемента закреплена установкой PARAM, AUTOSPC, YES PARAM, K6ROT, 100. стоит по умолчанию для нелинейных последовательностей решений

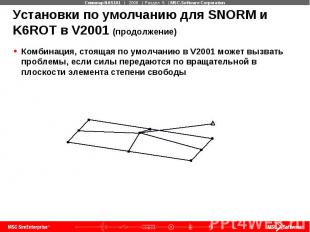
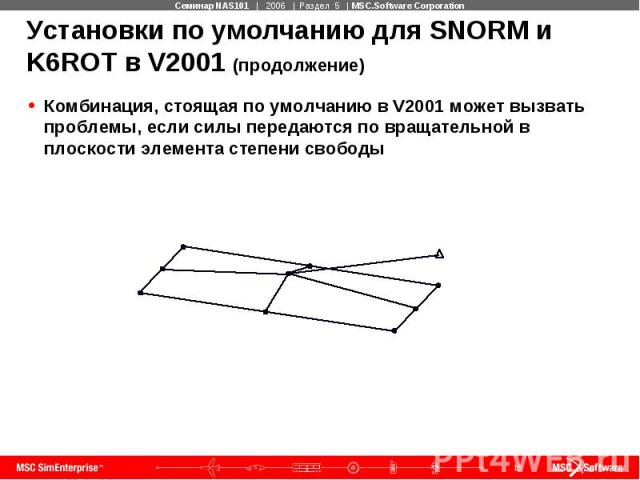
Установки по умолчанию для SNORM и K6ROT в V2001 (продолжение) Комбинация, стоящая по умолчанию в V2001 может вызвать проблемы, если силы передаются по вращательной в плоскости элемента степени свободы

Эффект от использования K6ROT – пример

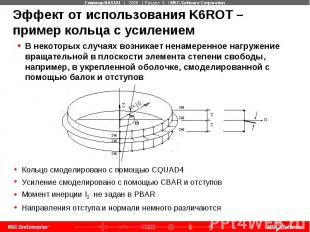
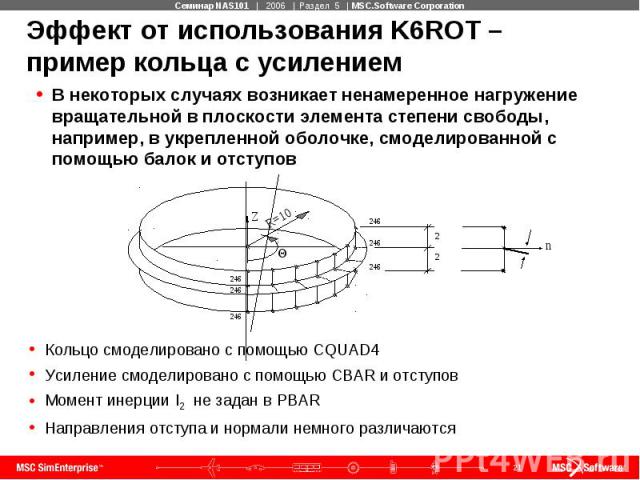
Эффект от использования K6ROT – пример кольца с усилением В некоторых случаях возникает ненамеренное нагружение вращательной в плоскости элемента степени свободы, например, в укрепленной оболочке, смоделированной с помощью балок и отступов

Эффект от использования K6ROT – пример кольца с усилением (продолжение)

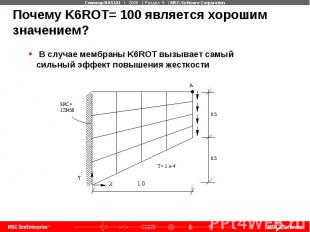
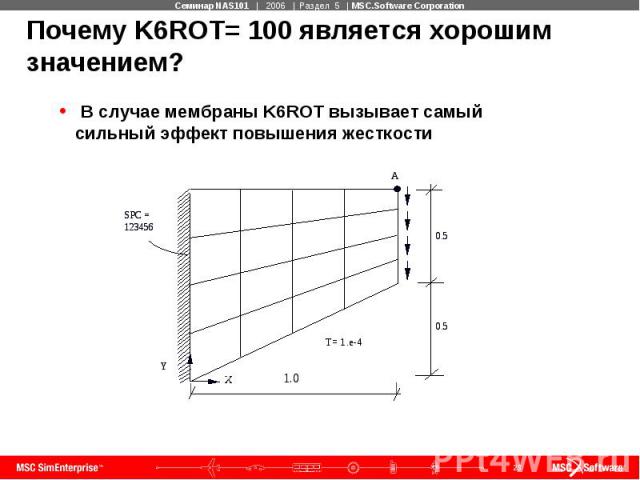
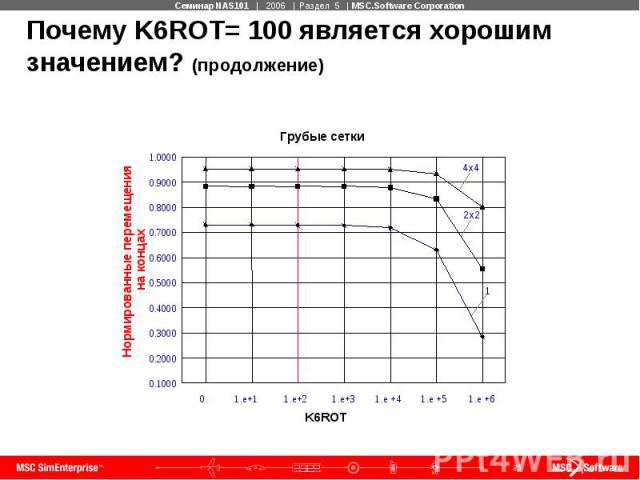
Почему K6ROT= 100 является хорошим значением? В случае мембраны K6ROT вызывает самый сильный эффект повышения жесткости

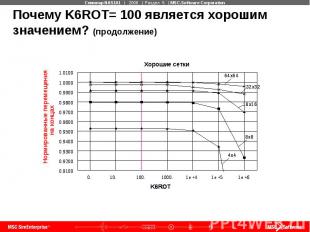
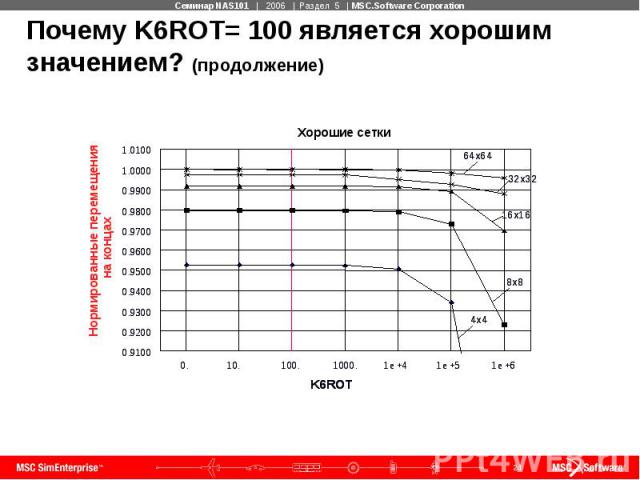
Почему K6ROT= 100 является хорошим значением? (продолжение)

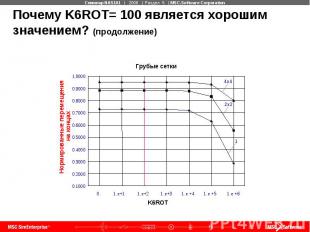
Почему K6ROT= 100 является хорошим значением? (продолжение)

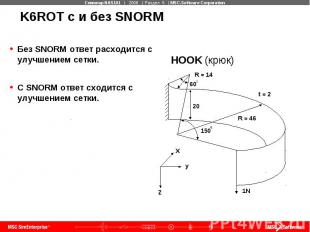
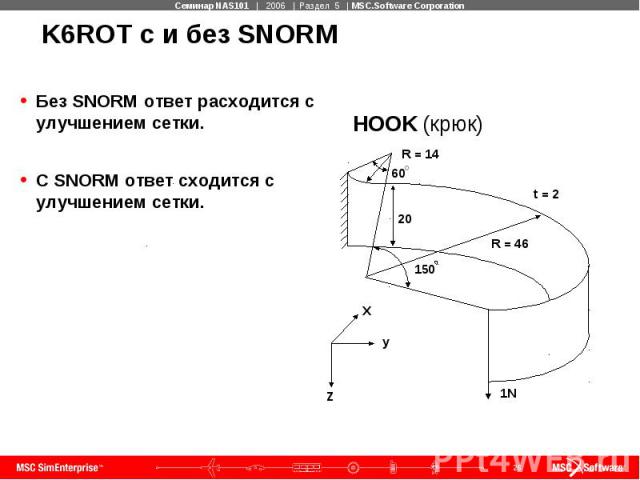
K6ROT с и без SNORM

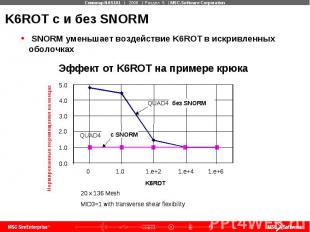
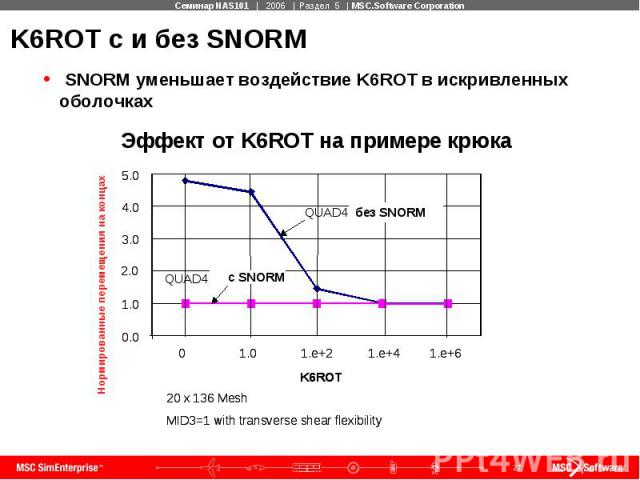
K6ROT с и без SNORM

Новые установки по умолчанию для K6ROT Мембранный тест показывает, что K6ROT=100 является наилучшим выбором. Стандартные тесты подтверждают, что K6ROT=100 не влияет на результат При использовании оболочечных нормалей (PARAM, SNORM, 20.) эффектом повышения жесткости можно пренебречь Когда оболочечные нормали выключены (PARAM, SNORM, 0.), K6ROT значительно влияет на жесткость в задачах с искривленными оболочками.

Новые установки по умолчанию для K6ROT (продолжение) K6ROT=100. Всегда стояло по умолчанию для нелинейных решений SOL 106 и 129 K6ROT=100. Соответствует значению жесткости, используемому другими конечноэлементными программами Если ожидается использование настроек v2001 K6ROT=0. , то: необходимо установить значение параметра по умолчанию в RC файле По умолчанию для всех последовательностей решений в v2004+: SNORM=20. K6ROT=100.

Замечания по поводу новых значений по умолчанию для K6ROT Для плоско-напряженных задач Для плоско-напряженных задач (только мембраны), Обычно закрепляют 6-ую степень свободы SPC 3456, если напряжения возникают в плоскости x-y Проблемы не возникают, если K6ROT=0. Конструкция заземляется, если 6-я степень свободы закрепляется и K6ROT=100. Не закрепляется 6 степень свободы, если K6ROT= 100, или устанавливается K6ROT=0 для плоско-напряженных задач В некоторых случаях из-за увеличения размера модели решение может занять немного больше времени Начиная с MSC Nastran 2005 r2, если PARAM, K6ROT больше нуля, то это значение будет использовано только для элементов, которые имеют как мембранную, так и изгибную жесткости. Жесткость по вращательной степени свободы от K6ROT удаляется у мембранных элементов Это решает проблему перезакрепления по 6й степени свободы.

Пример AUTOSPC Запустите входные файлы MSC NASTRAN Section5_1.bdf вариант solid элементов Оцените таблицу сингулярностей узлов Запустите входные файлы MSC NASTRAN Section5_3.bdf solid/plate комбинация Оцените таблицу сингулярностей узлов и проверьте наличие фатальных ошибок

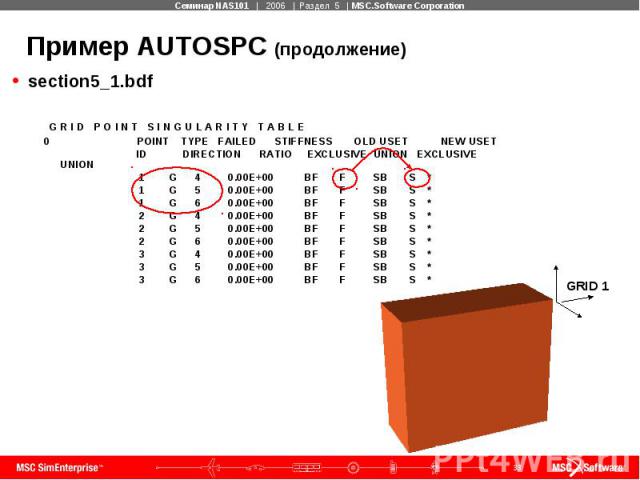
AUTOSPC Пример (продолжение) section5_1.bdf

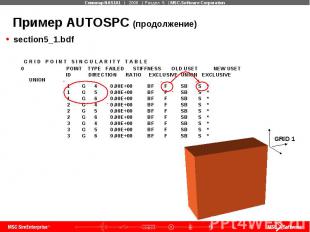
Пример AUTOSPC (продолжение) section5_1.bdf G R I D P O I N T S I N G U L A R I T Y T A B L E 0 POINT TYPE FAILED STIFFNESS OLD USET NEW USET ID DIRECTION RATIO EXCLUSIVE UNION EXCLUSIVE UNION 1 G 4 0.00E+00 BF F SB S * 1 G 5 0.00E+00 BF F SB S * 1 G 6 0.00E+00 BF F SB S * 2 G 4 0.00E+00 BF F SB S * 2 G 5 0.00E+00 BF F SB S * 2 G 6 0.00E+00 BF F SB S * 3 G 4 0.00E+00 BF F SB S * 3 G 5 0.00E+00 BF F SB S * 3 G 6 0.00E+00 BF F SB S *

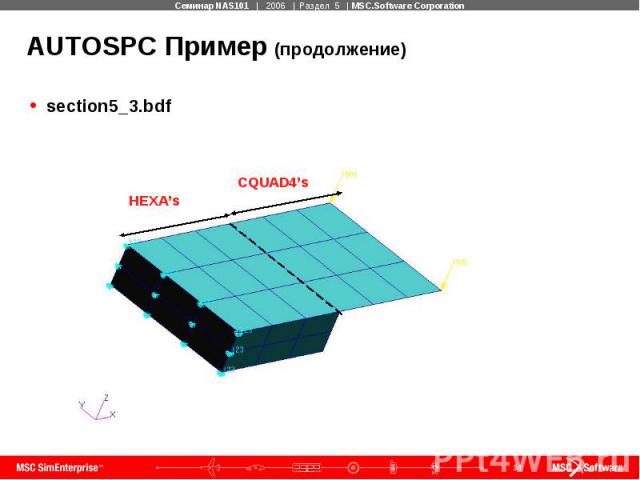
AUTOSPC Пример (продолжение) section5_3.bdf

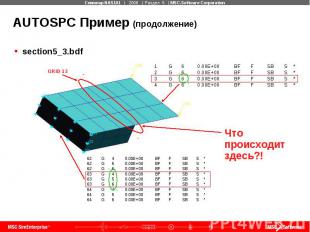
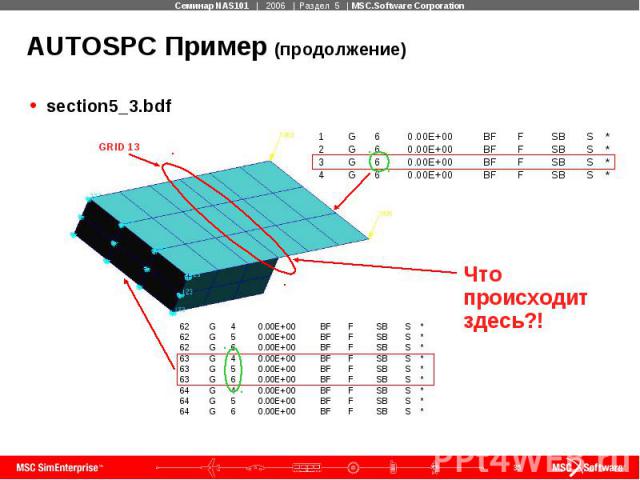
AUTOSPC Пример (продолжение) section5_3.bdf

AUTOSPC Пример (продолжение) section5_3.bdf THE FOLLOWING DEGREES OF FREEDOM HAVE FACTOR DIAGONAL RATIOS GREATER THAN 1.00000E+07 OR HAVE NEGATIVE TERMS ON THE FACTOR DIAGONAL. 0 SUBCASE 1 0 GRID POINT ID DEGREE OF FREEDOM MATRIX/FACTOR DIAGONAL RATIO MATRIX DIAGONAL 13 R2 1.71146E+13 2.13419E+02 ^^^ USER FATAL MESSAGE 9050 (SEKRRS) ^^^ RUN TERMINATED DUE TO EXCESSIVE PIVOT RATIOS IN MATRIX KLL. ^^^ USER ACTION: CONSTRAIN MECHANISMS WITH SPCI OR SUPORTI ENTRIES OR SPECIFY PARAM,BAILOUT,-1 TO CONTINUE THE RUN WITH MECHANISMS.

Диагностирование ошибок

Отладка модели Из предыдущего примера: Section5_3.bdf Результаты расчетов привели к фатальным ошибкам из-за наличия механизмов В данном разделе показано, как определить тип ошибки

Отладка модели (продолжение)

Отладка модели (продолжение)

Отладка модели (продолжение) Используя SPC или SPC1 записи, Исправьте входные файлы MSC NASTRAN Section5_3.bdf (подсказка: GRIDS 1 5 9 13 формируют соединение) Оцените результаты и последствия изменений

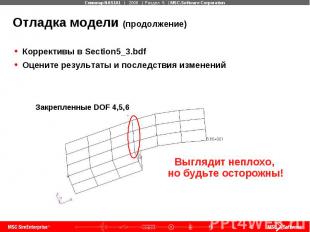
Отладка модели (продолжение) Коррективы в Section5_3.bdf Оцените результаты и последствия изменений

Отладка модели (продолжение) Коррективы в Section5_3.bdf Оцените результаты и последствия изменений

Отладка модели (продолжение) До сих пор мы рассматривали два примера с фатальными ошибками, вызванными наличием механизмов Сообщение о фатальной ошибке Fatal Message 9050 На практике существует большое количество проверок (как синтаксических так и общих данных), которые MSC Nastran будет выполнять для нахождения ошибок перед началом анализа, а также в ходе его проведения. Общий вид сообщений о фатальной ошибке будет одинаков. Ключевая информация - это номер сообщения и краткое описание. Более подробно о значениях фатальных ошибок можно узнать из Reference Guide или из On Line Encyclopedia

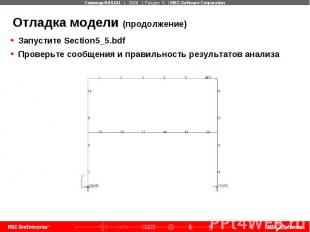
Отладка модели (продолжение) Запустите Section5_5.bdf Проверьте сообщения и правильность результатов анализа

Отладка модели (продолжение) Section5_5.f06 На какую характеристику группы элементов указывают предупреждающие сообщения (warning messages)? Что означает предупреждающее (warning) сообщение?

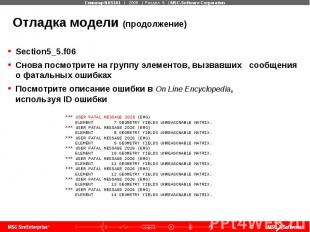
Отладка модели (продолжение) Section5_5.f06 Снова посмотрите на группу элементов, вызвавших сообщения о фатальных ошибках Посмотрите описание ошибки в On Line Encyclopedia, используя ID ошибки

Отладка модели (продолжение)

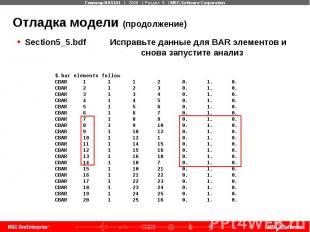
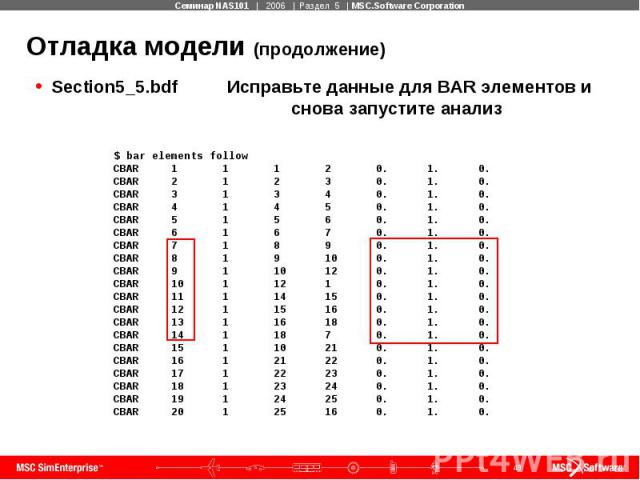
Отладка модели (продолжение) Section5_5.bdf Исправьте данные для BAR элементов и снова запустите анализ

Дальнейшая отладка модели Для более глубокого понимания значения файлов, которые могут использоваться при отладке, рассмотрим основные положения внутреннего языка MSC Nastran – DMAP. DMAP – Direct Matrix Abstraction Procedure Язык высокого уровня, на котором написан MSC Nastran Полностью открыт для просмотра и редактирования пользователем DMAP модули выполняют математические операции, требуемые для выполнения запрошенной при анализе последовательности решения.

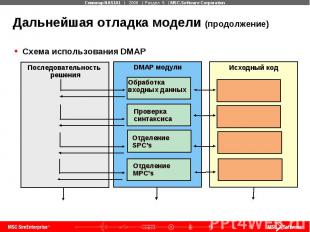
Дальнейшая отладка модели (продолжение) Схема использования DMAP

Дальнейшая отладка модели (продолжение) Описание файла .f04 Файл ".f04" содержит список выполнения модулей MSC Nastran используемых при решении задачи Каждый раз, когда выполняется какой-либо DMAP модуль, в файле .f04 печатается строка содержащая имя модуля и его текущее состояние

Дальнейшая отладка модели (продолжение) Если сообщения об ошибке не обеспечивают достаточного объяснения ее причины, пользователь может также проверить файл .f04 чтобы определить – в какой точке анализ был прерван. В общем случае, понимание выполнения последовательности DMAP модулей бывает достаточно сложным, но для специалистов MSC обеспечивающих поддержку своих пользователей эта информация может быть очень важной. 10:33:06 0:00 33.0 0.0 0.6 0.0 PHASE1DR 104 (S)DBSETOFF BEGN 10:33:06 0:00 33.0 0.0 0.6 0.0 PHASE1DR 106 (S)PHASE1A BEGN 10:33:06 0:00 33.0 0.0 0.7 0.0 PHASE1A 42 TA1 BEGN 10:33:06 0:00 34.0 1.0 0.7 0.0 PHASE1A 51 MSGHAN BEGN * 10:33:06 0:00 34.0 0.0 0.7 0.0 PHASE1A 52 (S)SEMG BEGN 10:33:06 0:00 34.0 0.0 0.7 0.0 SEMG 22 ELTPRT BEGN 10:33:06 0:00 34.0 0.0 0.7 0.0 SEMG 28 EMG BEGN 10:33:06 0:00 34.0 0.0 0.7 0.0 SEMG 36 (S)ERRPH1 BEGN 10:33:06 0:00 34.0 0.0 0.7 0.0 ERRPH1 19 (S)PRTSUM BEGN 10:33:06 0:00 34.0 0.0 0.7 0.0 PRTSUM 24 PROJVER BEGN 10:33:06 0:00 34.0 0.0 0.7 0.0 PRTSUM 25 DBDICT BEGN 10:33:06 0:00 34.0 0.0 0.7 0.0 PRTSUM 26 PRTPARM BEGN 10:33:06 0:00 34.0 0.0 0.7 0.0 ERRPH1 20 EXIT BEGN 10:33:06 0:00 34.0 0.0 0.7 0.0 XSEMDR END

Основные виды проверок

Основные виды проверок В предыдущем разделе мы рассматривали способ исправления ошибок: Отладка В этом разделе мы поговорим об их предотвращении: Основные виды проверок Практика правильного моделирования

Основные виды проверок (продолжение) Перед анализом Искаженная форма элементов Используйте препроцессор для визуальной проверки правильности формы элементов Обратите внимание на предупреждающие сообщения (WARNING messages) в файле .f06 Согласованность единиц измерения модели Проверка по силе: СИЛА = МАССА * УСКОРЕНИЕ

Основные виды проверок (продолжение) Искаженная форма элементов Соотношение сторон Соотношение сторон должно быть меньше, чем 4:1 (более низкое для мест с высоким градиентом напряжений). В случае одноосных полей напряжений допустимы большие отношения сторон.

Основные виды проверок (продолжение) Искаженная форма элементов Наклон Четырехугольные элементы должны быть близки к квадрату настолько, насколько это возможно.

Основные виды проверок (продолжение) Искаженная форма элементов Трапеция (2 направления)

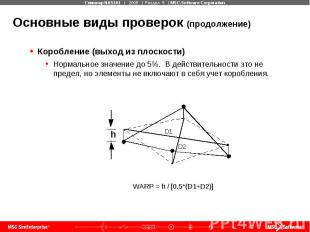
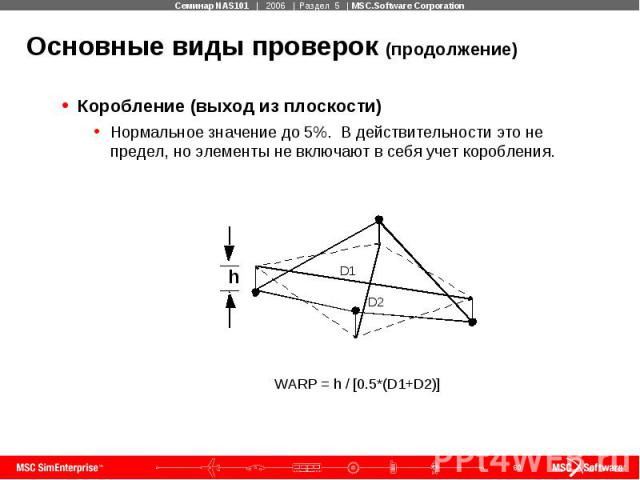
Основные виды проверок (продолжение) Коробление (выход из плоскости) Нормальное значение до 5%. В действительности это не предел, но элементы не включают в себя учет коробления.

Основные виды проверок (продолжение) После анализа Значение эпсилон (погрешности) Суммирование приложенных нагрузок Суммирование сил реакции Значения энергии деформации Максимальные перемещения

Основные виды проверок (продолжение) После анализа - Значение Эпсилон

Основные виды проверок (продолжение) Если эта величина 10-6 ,и больше, это значит, что модель плохо обусловлена. Для каждого типа конструкции, модели и расчета Посмотрите значение эпсилон после Сравните с допустимыми значениями

Основные виды проверок (продолжение) После анализа – Суммирование приложенных нагрузок Используйте запрос OLOAD в секции Case Control Особенно важно для: Инерционных нагрузок Сложной нагрузки давлением Сложной распределенной нагрузки

Основные виды проверок (продолжение) Проверка приложенных нагрузок

Основные виды проверок (продолжение) Пост анализ – Суммирование реакций Проверка, что направление противоположно и балансирует OLOAD сумму

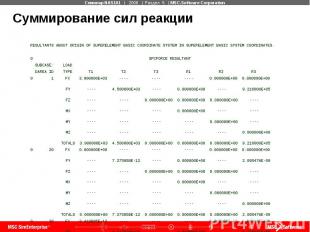
Суммирование сил реакции

Проверка равновесия Проверка равновесия является одной из самых важных проверок в статическом анализе F = 0 M = 0 Раньше можно было получить результаты OLOAD, SPCFORCE и MPCFORCE и вручную их использовать для проверки равновесия Теперь в секции Case Control появилась команда Equilibrium, запрашивающая автоматическую проверку равновесия Возможно только для статического анализа

Проверка равновесия (продолжение) Формат:

Проверка равновесия (продолжение)

Проверка действительных приложенных нагрузок Запрос на вывод нагрузок в точках приложения OLOAD = n Для некоторых типов нагружения могут создаваться большие объемы выходных данных Например, гравитационная нагрузка в больших моделях

Проверка действительных приложенных нагрузок (продолжение)

Основные виды проверок (продолжение) После анализа – Суммирование сил реакции Проверьте, что значения соответствуют и уравнивают суммарные приложенные нагрузки

Основные виды проверок (продолжение) Проверка сил реакций

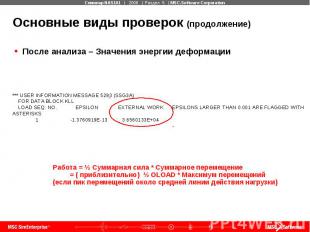
Основные виды проверок (продолжение) После анализа – Значения энергии деформации

Основные виды проверок (продолжение) После анализа – Максимальные перемещения Укажите PARAM,PRTMAXIM,YES для этой распечатки Номер узла (GRID ID) не печатается, и может быть разным для каждой степени свободы 0 MAXIMUM DISPLACEMENTS 0 T1 T2 T3 R1 R2 R3 0 1 3.0938861E-07 4.1483727E-08 3.6560131E+01 7.2180829E+00 5.6827263E+01 0.0000000E+00

Основные виды проверок. Пример Запустите section5_6.bdf Выполните следующие проверки: Значение эпсилон Суммирование приложенных нагрузок Суммирование сил реакции Значения энергии деформации Максимальные перемещения

Практика моделирования

Практика моделирования Основные моменты: Плотность сетки – должна соответствовать поставленным целям Качество сетки – должно соответствовать поставленным целям Нагружение Граничные условия

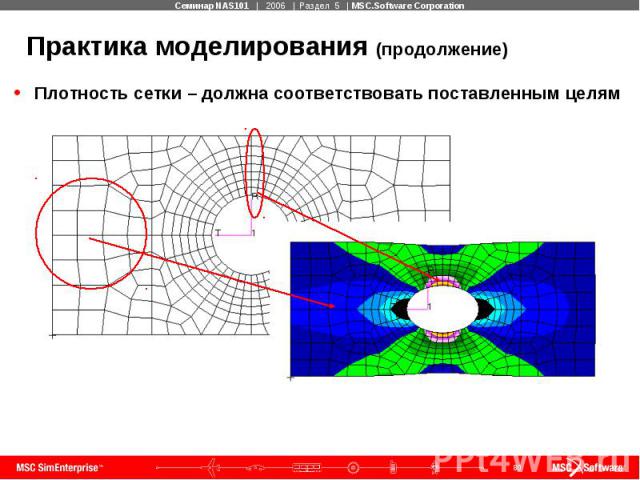
Практика моделирования (продолжение) Плотность сетки – должна соответствовать поставленным целям

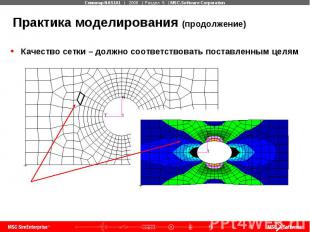
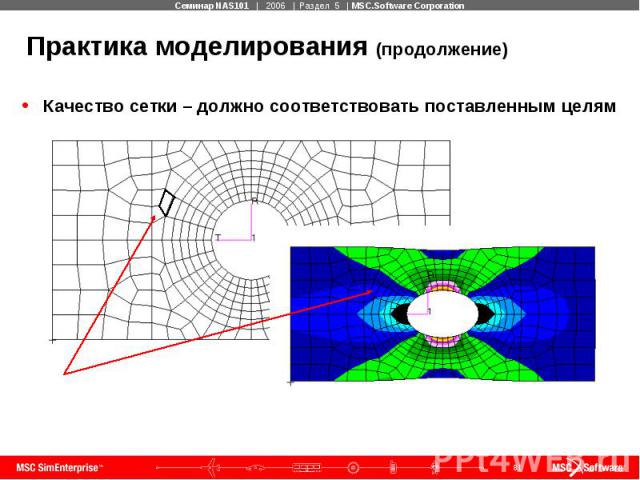
Практика моделирования (продолжение) Качество сетки – должно соответствовать поставленным целям

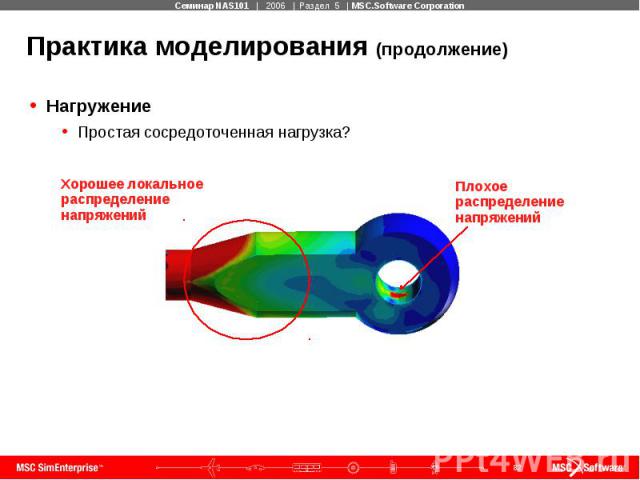
Практика моделирования (продолжение) Нагружение Простая сосредоточенная нагрузка?

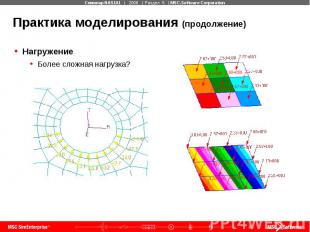
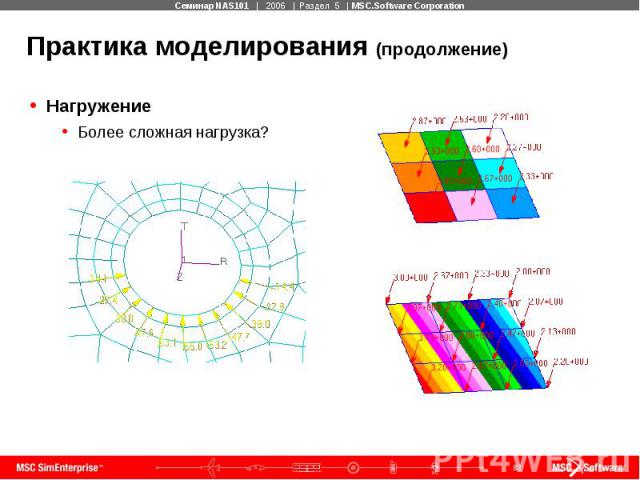
Практика моделирования (продолжение) Нагружение Более сложная нагрузка?

Практика моделирования (продолжение) Граничные условия Неправильное определение выходной системы координат для SPC, MPC и RIGID элементов может "испортить" модель Чрезмерное закрепление модели может привести к большему влиянию сдвиговых напряжений через коэффициент Пуассона. Эти напряжения могут сильно исказить действительное поле напряжений Закрепление (или сила) в одном узле приводит к сингулярности в поле напряжения. Результаты расчета напряжений в этой точке вероятно будут ошибочными.

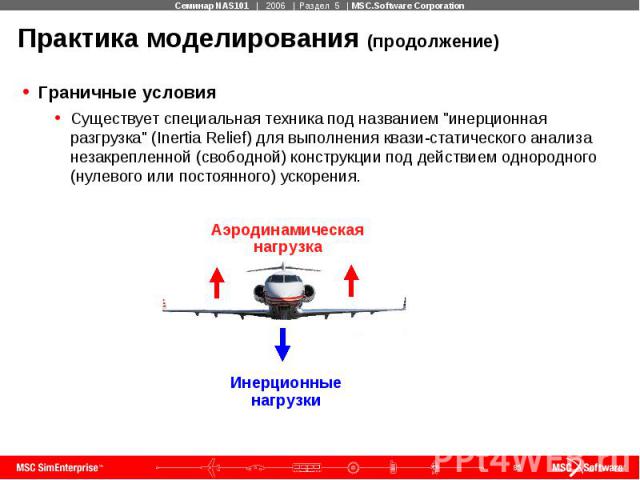
Практика моделирования (продолжение) Граничные условия Существует специальная техника под названием "инерционная разгрузка" (Inertia Relief) для выполнения квази-статического анализа незакрепленной (свободной) конструкции под действием однородного (нулевого или постоянного) ускорения.

MPC - граничные условия для группы узлов Rigid (жесткие) элементы

Граничные условия для группы узлов Граничные условия для группы узлов (MPC) задаются пользователем в виде линейного уравнения, которое задает соотношения между перемещениями по степеням свободы. MPC полезно использовать для: Определения относительного смещения двух и более узловых точек по заданным степеням свободы Соединения различных типов элементов; например, соединения элементов, которые имеют вращательные степени свободы с элементами, которые имеют только поступательные степени свободы (оболочки с объемными элементами) Распределения нагрузки в нескольких точках конструкции Моделирования жестких связей между узлами

Граничные условия для группы узлов (продолжение) Предположим, узлы 145 и 146 должны двигаться вместе в направлениях x и y (могут быть чем-либо соединены)

Граничные условия для группы узлов (продолжение) $ SID GRID DOF A1 GRID DOF A2 MPC 1 145 1 -1. 146 1 1. MPC 1 145 2 -1. 146 2 1.

Граничные условия в виде жестких элементов (R-тип) MSC NASTRAN содержит несколько наиболее часто используемых MPC-соотношений в форме различных элементов R-типа. Во избежание ошибок, настоятельно рекомендуется пользователям, плохо владеющим техникой записи MPC- соотношений, применять жесткие элементы (элементы R-типа) там, где это возможно. В отличии от MPC, элементы R-типа не выбираются в секции CASE CONTROL. Они описываются только в секции BULK DATA следующими записями: Два типа элементов R-типа: линейные лагранжевы (действительные элементы, , дифференциальная жесткость)

Жесткие (Rigid) элементы RBAR - Жесткий балочный элемент с шестью степенями свободы на каждом конце RBE2 - Жесткое тело связанное с произвольным числом узлов RBE3 - Определяет граничное уравнение, в котором движение "ссылочного" узла является средневзвешенным значением движения других узлов

Формат RBAR GA, GB – узлы A и B соответственно CNA, CNB – независимые степени свободы на концах A и B соответственно CMA, CMB – зависимые степени свободы на концах A и B соответственно ALPHA – тепловой коэффициент расширения (доступен только с включенной опцией Lagrange, см. дальше)

Формат RBE2 GN – независимый узел GM – зависимый узел CM – компоненты в зависимых узлах ALPHA—тепловой коэффициент расширения (доступен только с включенной опцией Lagrange, см. дальше)

Формат RBE3

Формат RBE3 (продолжение) REFGRID – Опорный узел REFC – компоненты, определенные на REFGRID WTi – весовые факторы Ci – компоненты с весовым фактором Wti в узле Gi,j Gi,j – узловые точки с компонентами Ci, содержащие в уравнении весовой фактор Wti ALPHA—тепловой коэффициент расширения (доступен только с включенной опцией Lagrange, см. дальше)

Жесткие (Rigid) элементы (продолжение) RSPLINE Определяет граничное уравнение коэффициенты которого определяются перемещениями и углами наклона гибкой трубчатой балки RSSCON Используется для соединения Plate элементов с Solid элементами В разделе 2.10 MSC NASTRAN Application Manual приведены 10 примеров использования элементов R-типа и два примера использования MPC.

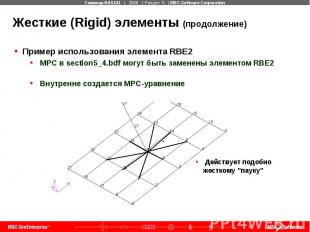
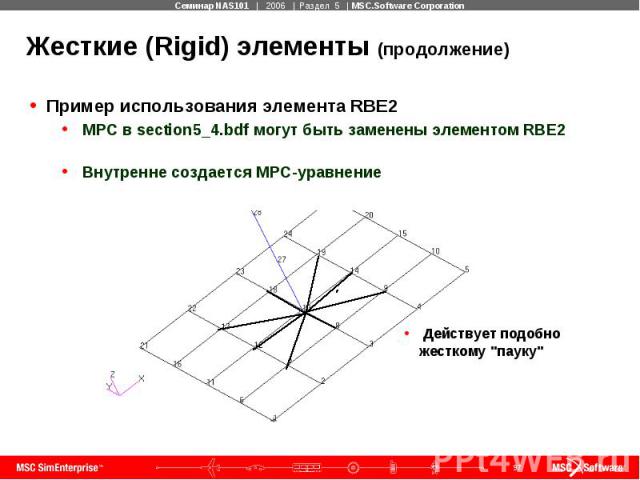
Жесткие (Rigid) элементы (продолжение) Пример использования элемента RBE2 MPC в section5_4.bdf могут быть заменены элементом RBE2 Внутренне создается MPC-уравнение

Жесткие (Rigid) элементы (продолжение) Пример использования элемента RBE2 Степени свободы центра "паука" являются независимыми степенями свободы Другие степени свободы являются зависимыми и не должны иметь перекрестных связей

Жесткие (Rigid) элементы (продолжение) Пример использования элемента RBE2

Жесткие (Rigid) элементы (продолжение) Примеры использования элемента RBE2 Соединения при упрощении моделей Блок двигателя Параболическая антенна Соединение областей с различной сеткой Более точная модель, например, фланца с грубой моделью вала

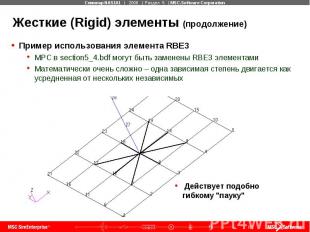
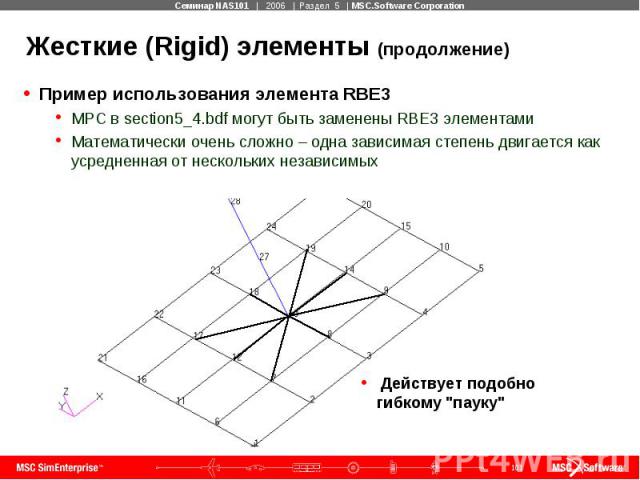
Жесткие (Rigid) элементы (продолжение) Пример использования элемента RBE3 MPC в section5_4.bdf могут быть заменены RBE3 элементами Математически очень сложно – одна зависимая степень двигается как усредненная от нескольких независимых

Жесткие (Rigid) элементы (продолжение) Пример использования элемента RBE3 Степени свободы центра "паука" являются зависимыми степенями свободы Другие степени свободы являются независимыми и могут иметь перекрестную связь

Жесткие (Rigid) элементы (продолжение) RBE3 математически очень сложен – одно зависимое движение как среднее от множества независимых Примеры использования элемента RBE3: Соединения при упрощении моделей Параболическая антенна Соединение областей с различной сеткой Фюзеляж из балок и пластин – гибкая овализация фюзеляжа Присоединение полезной нагрузки Распределяет полезную нагрузку по требуемым узлам ее присоединения

Жесткие элементы (пример) Используйте файл section5_3.bdf Попробуйте модифицировать его с использованием: RBAR RBE2 RBE3 Сравните распределение перемещений

Жесткие элементы RSSCON

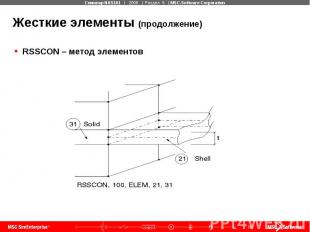
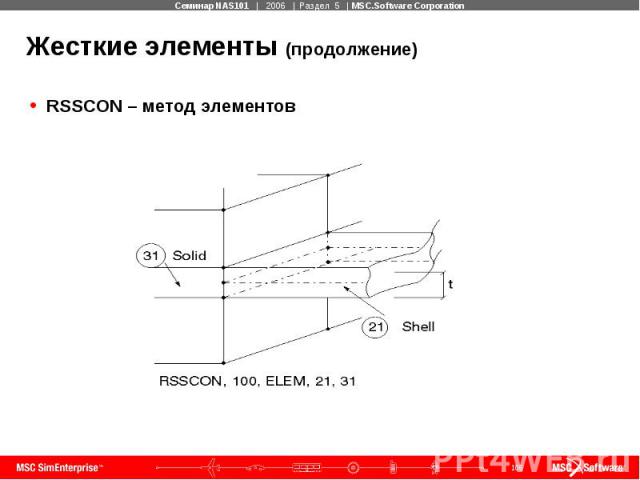
Жесткие элементы (продолжение) RSSCON – метод элементов

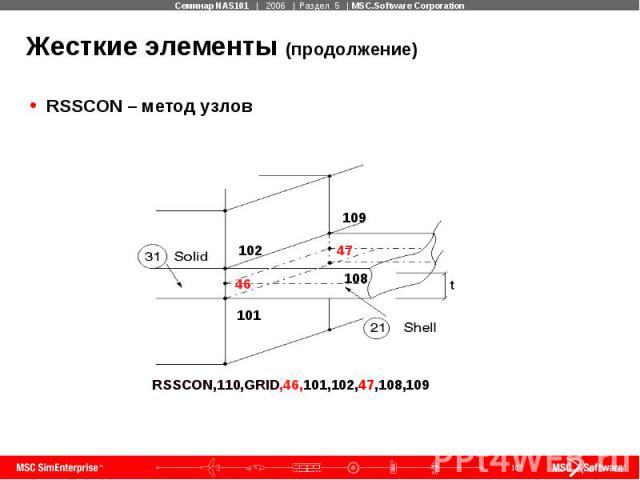
Жесткие элементы (продолжение) RSSCON – метод узлов

Жесткие элементы (продолжение) Используйте файл section5_3.bdf Попробуйте модифицировать его с использованием: RSSCON – узловой метод RSSCON – метод элементов Сравните распределение перемещений

Усовершенствования жестких элементов (v2004) До MSC Nastran 2004 жесткие элементы (например, RBAR и т.д.) были линейными элементами В MSC Nastran 2004 введен новый тип жестких элементов – лагранжевы элементы Линейные жесткие элементы обладают следующими ограничениями: Не вычисляют тепловые нагрузки Не обладают дифференциальной матрицей жесткости, что ведет к неправильным результатам в задачах, требующих ее (например, анализ устойчивости) Используют теорию малых вращений, что ведет к неправильным результатам в геометрически нелинейном анализе Используют метод уменьшения, приводящую к плотным матрицам

Усовершенствования жестких элементов (v2004) (продолжение) На лагранжевы жесткие элементы не обладают ограничениями, накладываемыми на линейные элементы (перечислены на предыдущем слайде) Лагранжевы жесткие элементы похожи на “реальные элементы” с матрицей жесткости вместо MPC, включая возможность поля ( – коэффициент температурного расширения) В зависимости от самого лагранжева жесткого элемента к нему добавляется 1-6 степеней свобод множителей Лагранжа например, у RROD 1 степень свободы множителя Лагранжа, у RBAR – от 1 до 6

Усовершенствования жестких элементов (v2004) (продолжение) Два типа методов множителей Лагранжа Расширенный метод множителей Лагранжа (предпочитаемый метод) Независимые степени свободы, зависимые степени свободы, и степени свободы множителей Лагранжа хранятся в наборе решений (l-set) Сохраняется разреженность матрицы Возможен для решений SOL 101, 103, 105 и 400 Метод исключений Лагранжа (вспомогательный метод) И зависимые степени свободы, и степени свободы множителей Лагранжа исключаются из глобальной матрицы жесткости и помещаются в mr-set Теряется разреженность матрицы Возможен для решений SOL 101, 103 и 105

Усовершенствования жестких элементов (v2004) (продолжение) По умолчанию используются линейные жесткие элементы Для выбора лагранжевых жестких элементов в секцию Case Control добавлена новая команда LINEAR RIGID = LAGR LGELIM где LINEAR – линейный жесткий элемент (по умолчанию) LAGR – расширенный жесткий элемент Лагранжа LGELIM – метод исключений Лагранжа

Усовершенствования жестких элементов (v2004) (продолжение) Существующие линейные жесткие элементы – RBAR, RBE1, RBE2, RBE3, RROD и RTRPLT – поддерживают новые жесткие элементы Лагранжа (активизируется командой RIGID секции Case Control) Добавлены три новых жестких элемента: RBAR1 RTRPLT1 RJOINT Все Rtype элементы могут использоваться как в линейном, так и в лагранжевом формализмах Входные данные по элементу различаются для двух методов

Усовершенствования жестких элементов (v2004) (продолжение) RBAR Линейный жесткий элемент Независимые степени свободы назначаются и на CAN, и на CNB Жесткий элемент Лагранжа Независимые степени свободы должны быть назначениы на одну точку По умолчанию CNA=123456 и CMB=123456 Аналогичные правила действуют для элементов RBE1, RBE2 и RTRPLT

Усовершенствования жестких элементов (v2004) (продолжение) RBAR1 (новая альтернативная форма RBAR) Все 6 степеней свободы на GA являются независимыми Зависимые степени свободы узла GB определяются в поле CMB Предпочтительно для жестких элементов Лагранжа RTRPLT1 (новая альтернативная форма RTRPLT) Все 6 степеней свободы на GA являются независимыми Зависимые степени свободы на узлах GB и GC определяются в полях CMB и CMC соответственно

Усовершенствования жестких элементов (v2004) (продолжение) RROD Линейный жесткий элемент Выбирает одну зависимую степень свободы на CMA или CMB Жесткий элемент Лагранжа Выбирает одну зависимую степень свободы на CMA или CMB или позволяет MSC Nastran выбрать зависимую степень свободы автоматически (рекомендуется) RBE3 Линейный жесткий элемент REFC – любая комбинация из чисел от 1 до 6 (например, 126, 12356, и т.д.) Жесткий элемент Лагранжа REFC должен быть 123, 456 или 123456

Усовершенствования жестких элементов (v2004) (продолжение) RJOINT Формат нового жесткого элемента: Все 6 степеней свободы на GA независимы GB является зависимым узлом CB зависимая степень свободы для узла GB Нулевая длина между GA и GB Если CB=123456 или пустое, тогда GA и GB двигаются как одна точка Если GA и GB имеют разные выходные системы координат, CB использует систем координат GB

Усовершенствования жестких элементов (v2004) (продолжение) RJOINT (продолжение) Если одна из степеней свободы отсутствует в поле CB, RJOINT становится механизмом Шарнир – свободное вращение вокруг одной оси CB=12356, 12345 или 12346 Кардан – свободное вращение вокруг двух осей CB=1234, 1235 или 1236 Сферическое соединение – свободное вращение вокруг трех осей CB=123 Призматическое соединение – 2 блока, которые могут вращаться одинаково и перемещаться друг относительно друга вдоль локальной оси CB=23456, 13456 или 12456 Цилиндрическое соединение – механическая система, в которой 2 узловые точки могут иметь относительное перемещение и вращение вдоль подвижной оси CB=2356, 1346, 1245

Общая информация о модели

ELSUM Команда ELSUM секции Case Control выводит обобщенную информацию о запрошенных элементах Распечатка включает в себя Номера элементов Номер материала Длину или толщину Площадь Объем Конструкционную массу Не конструкционную массу Общую массу Общий вес

Вывод общей информации по элементу (ELSUM) Команда ELSUM предоставляет общую информацию по элементу (например, длина, масса и т.д.) ALL ELSUM (EID, PID, BOTH PIDSUM,EIDSUM) = n NONE

Вывод общей информации по элементу (ELSUM) Типичный вид выходного файла (продолжение):

MAX/MIN для перемещений и сил реакций В решении SOL 101 существует опция для вывода MAX/MIN значений перемещений и сил реакций для каждого варианта (SUBCASE) Если запрос сделан, то распечатка добавляется к стандартному выводу результатов

MAX/MIN для перемещений и сил реакций $ file maxmin.dat sol 101 cend title = cantilever beam model subtitle = OLOAD OUTPUT spc = 1 disp=all maxmin(vmag=2,disp,spcf)=all subcase 1 label = pload1 load = 1 subcase 2 label = load in x, y, and z load = 2 begin bulk pload1,1,1,fy,fr,0.,1.,1.,1. =,=,*(1),== =(6) force,2,9,,1.,1.,1.,1. PARAM GRDPNT 0 PARAM POST -1 $ cord2r,1,,0.,0.,0.,0.,1.,0. ,1.,0.,1.

MAX/MIN для перемещений и сил реакций 0 *** T1 *** D I S P L A C E M E N T M A X / M I N V A L U E S U M M A R Y RESULTS FOR SUBCASE 1 MAXMIN OPTIONS: SET=ALL, CID=BASIC, VMAG=2, VMAG=2, COMP=T1 POINT ID. TYPE CID ***TMAG*** T2 T3 R1 R2 R3 1 G BASIC 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 2 G BASIC 5.404634E-02 0.000000E+00 0.000000E+00 8.251953E-03 0.000000E+00 0.000000E+00 8 G BASIC 1.563420E+00 0.000000E+00 0.000000E+00 2.495117E-02 0.000000E+00 0.000000E+00 9 G BASIC 1.875780E+00 0.000000E+00 0.000000E+00 2.500000E-02 0.000000E+00 0.000000E+00 9 G 1 0.000000E+00 0.000000E+00 1.875780E+00 1.767767E-02 -1.767767E-02 0.000000E+00 1 CANTILEVER BEAM MODEL FEBRUARY 13, 2001 MSC.NASTRAN 1/17/01 PAGE 12 OLOAD OUTPUT 0 0 *** R1 *** D I S P L A C E M E N T M A X / M I N V A L U E S U M M A R Y RESULTS FOR SUBCASE 1 MAXMIN OPTIONS: SET=ALL, CID=BASIC, VMAG=2, VMAG=2, COMP=R1 POINT ID. TYPE CID T1 T2 T3 ***RMAG*** R2 R3 1 G BASIC 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 0.000000E+00 2 G BASIC 5.404634E-02 0.000000E+00 0.000000E+00 8.251953E-03 0.000000E+00 0.000000E+00 8 G BASIC 1.563420E+00 0.000000E+00 0.000000E+00 2.495117E-02 0.000000E+00 0.000000E+00 9 G BASIC 1.875780E+00 0.000000E+00 0.000000E+00 2.500000E-02 0.000000E+00 0.000000E+00 9 G 1 0.000000E+00 0.000000E+00 1.875780E+00 1.767767E-02 -1.767767E-02 0.000000E+00

Проверка геометрии элементов

Проверка геометрии элементов Препроцессоры могут генерировать сетку с плохой геометрией элементов (соотношение сторон, наклон, выход из плоскости и т.п.) Ранее печаталось отдельное сообщение для каждого элемента, который не удовлетворял рекомендациям MSC Nastran (это часто приводило к большому количеству сообщений, которые большинство пользователей игнорировало) Сейчас существует опция, позволяющая управлять этими сообщениями (т.е. можно их проигнорировать, запретив печать, но делать это НЕ РЕКОМЕНДУЕТСЯ) Управление происходит с помощью команды GEOMCHECK секции Executive Control

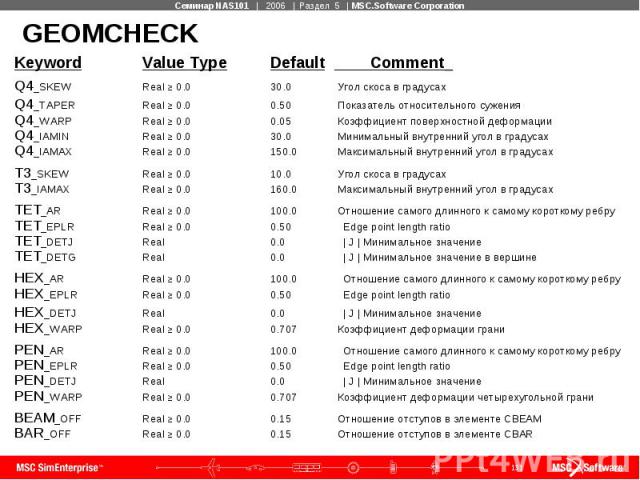
GEOMCHECK Проверки доступны только для следующих элементов: Тип элемента Ключевое слово Число тестов CQUAD4, CQUADR Q4_... 5 CTRIA3, CTRIAR T3_… 2 CTETRA TET_... 4 CHEXA HEX_... 4 CPENTA PEN_... 4 CBEAM BEAM_... 1 CBAR BAR_... 1 Всего: 21 Может быть записано несколько команд GEOMCHECK в одном файле. Карты продолжения поддерживаются.

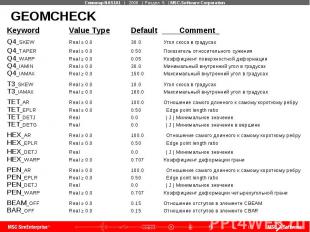
Проверка геометрии элементов Примеры: 1. Установка значения погрешности скоса угла в элементе CQUAD4 на 15 градусов и минимального значения сообщений 50 GEOMCHECK Q4_SKEW=15.0,MSGLIMIT=50 2. Установка минимального количества сообщений для каждого типа элементов на 500 GEOMCHECK MSGLIMIT = 500 3. Запрос сообщений об ошибке при определении относительного сужения в элементе CQUAD4 GEOMCHECK Q4_TAPER,MSGTYPE=FATAL 4. Запрос на вывод результатов всех тестов с использованием погрешностей по умолчанию GEOMCHECK SUMMARY

Эквивалентные константы NASTRAN и их значения по умолчанию NASTRAN Q4SKEW = 30. или NASTRAN SYSTEM (190) = 30. (см. ключевое слово Q4_SKEW команды GEOMCHECK) NASTRAN Q4TAPER = 0.5 или NASTRAN SYSTEM (189) = 0.5 (см. ключевое слово Q4_TAPER команды GEOMCHECK) NASTRAN T3SKEW = 10. или NASTRAN SYSTEM (218) = 10. (см. ключевое слово T3_SKEW команды GEOMCHECK) NASTRAN TETRAAR = 100. или NASTRAN SYSTEM (191) = 100. (см. ключевое слово TET_AR команды GEOMCHECK)

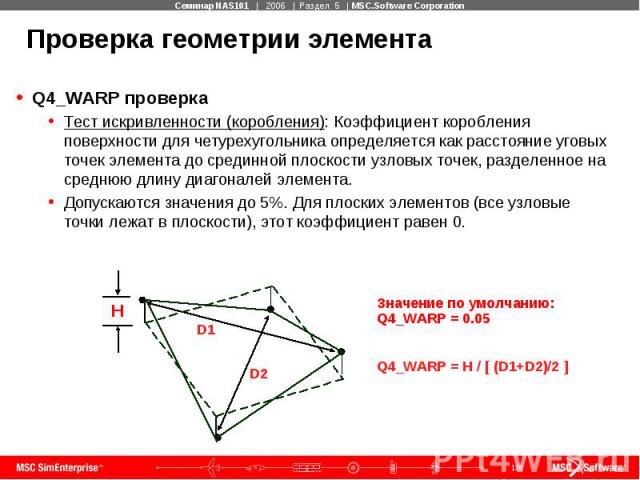
Проверка геометрии элемента Q4_Skew проверка Тест скошенности: Угол скошенности для четырехугольного элемента определяется как угол между линиями, которые соединяют срединный точки противоположных сторон четырехугольника. Четырехугольные элементы по форме должны быть как можно ближе к квадрату. При отсутствии скошенности, угол скошенности равен 90о.

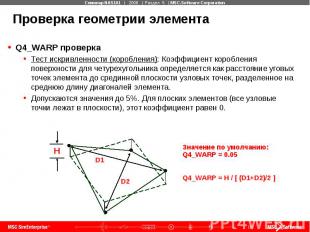
Проверка геометрии элемента Q4_Taper проверка Тест сужения (трапециевидности): Коэффициент сужения для четырехугольного элемента определяется как отношение площади треугольника, построенного по трем узловым точкам к половине площади четырехугольника. Наибольшее из четырех отношений сравнивается с допускаемым значением.

Проверка геометрии элемента

Проверка геометрии элемента

Проверка геометрии элемента TET_AR , HEX_AR и PEN_AR проверки Тест удлинения: Этот тест дает оценку отношения наибольшей длины (ребра или высоты) к наименьшей длине (ребра или высоты) в элементе. Удлинение – Aspect ratio (AR) должно быть меньше примерно 4:1 (как можно меньше в областях модели, где выкокий градиент напряжений). В случаях возникновения напряженно-деформированного состояния близкого к одноосному, допускаются большие значения.

Проверка геометрии элемента

TET_DETJ , HEX_DETJ и PEN_DETJ проверка Тест определителя Якобиана в точках интегрирования: Этот тест дает оценку определителя Якобиана в каждой точке интегрирования. Если он равен нулю или меняет знак от одной точки интегрирования к другой, то выдается информационное сообщение. Внимание! Нулевое значение признак ошибки, т.к. матрицы конечного элемента полученные с такой геометрии редко дают удовлетворительные результаты расчета. Значения по умолчанию: TET_DETJ = HEX_DETJ = PEN_DETJ = 0. TET_DETG проверка Тест определителя Якобиана в узловых точках: Этот тест применим только для элементов СTETRA. Этот тест такой же, что был рассмотрен ранее, за исключением того, что он использует положение угловых узлов. Если любой определитель равен нулю или меняет знак, то выдается информационное сообщение. Значение по умолчанию : TET_DETG = 0.

HEX_WARP и PEN_WARP проверка Тест кривизны грани: Этот тест применим для элементов CHEXA и CPENTA. Коэффициент кривизны грани - это косинус угла между векторами нормалей в противоположных угловых точках на каждой грани. Для грани у которой все четыре угловые точки лежат в одной плоскости, значение равно 1. Заданная по умолчанию точность допускает углы до 45o, прежде чем будет сгенерировано информационное сообщение.

Проверки BEAM_OFF и BAR_OFF Тест отступов: Этот тест применим для CBEAM и CBAR элементов. Длина отступа элемента сравнивается с реальной длиной элемента. Если отношение этих длин больше, чем точность, то выдается информационное сообщение, идентифицирующее элемент и его длину с и без эффекта отступов.

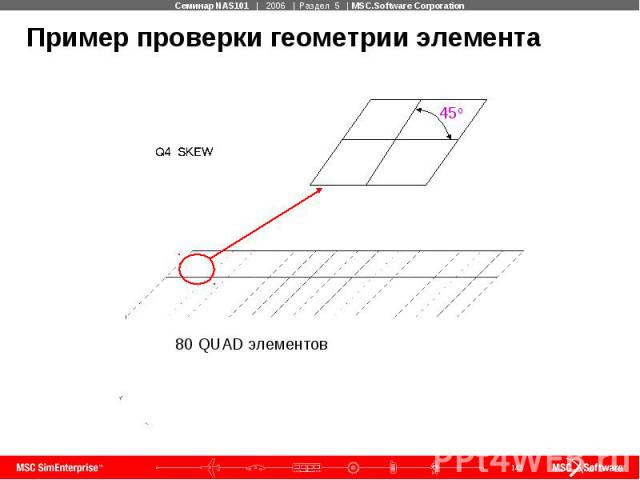
Пример проверки геометрии элемента

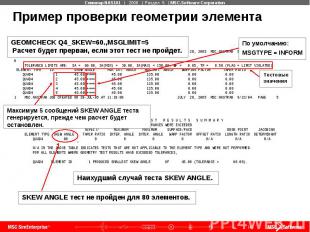
Пример проверки геометрии элемента Пример: GEOMCHECK Q4_SKEW=60.,MSGLIMIT=5 Идеальное значение угла SKEW (скошенности) равно 90о. Тест будет генерировать сообщение для любого значения меньше, чем 60о. Только 5 сообщений будет сгенерировано. Значение по умолчанию MSGTYPE: MSGTYPPE=INFORM, ++++ - индикатор для этого типа. Расчет не будет прерван независимо от того, прошел этот тест или нет.

Пример проверки геометрии элемента

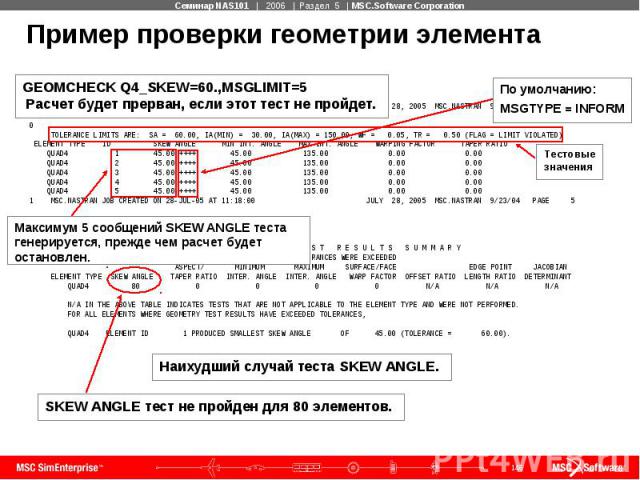
Пример проверки геометрии элемента 1 MSC.NASTRAN JOB CREATED ON 28-JUL-05 AT 11:18:00 JULY 28, 2005 MSC.NASTRAN 9/23/04 PAGE 4 0 TOLERANCE LIMITS ARE: SA = 60.00, IA(MIN) = 30.00, IA(MAX) = 150.00, WF = 0.05, TR = 0.50 (FLAG = LIMIT VIOLATED) ELEMENT TYPE ID SKEW ANGLE MIN INT. ANGLE MAX INT. ANGLE WARPING FACTOR TAPER RATIO QUAD4 1 45.00 ++++ 45.00 135.00 0.00 0.00 QUAD4 2 45.00 ++++ 45.00 135.00 0.00 0.00 QUAD4 3 45.00 ++++ 45.00 135.00 0.00 0.00 QUAD4 4 45.00 ++++ 45.00 135.00 0.00 0.00 QUAD4 5 45.00 ++++ 45.00 135.00 0.00 0.00 1 MSC.NASTRAN JOB CREATED ON 28-JUL-05 AT 11:18:00 JULY 28, 2005 MSC.NASTRAN 9/23/04 PAGE 5 0 E L E M E N T G E O M E T R Y T E S T R E S U L T S S U M M A R Y TOTAL NUMBER OF TIMES TOLERANCES WERE EXCEEDED ASPECT/ MINIMUM MAXIMUM SURFACE/FACE EDGE POINT JACOBIAN ELEMENT TYPE SKEW ANGLE TAPER RATIO INTER. ANGLE INTER. ANGLE WARP FACTOR OFFSET RATIO LENGTH RATIO DETERMINANT QUAD4 80 0 0 0 0 N/A N/A N/A N/A IN THE ABOVE TABLE INDICATES TESTS THAT ARE NOT APPLICABLE TO THE ELEMENT TYPE AND WERE NOT PERFORMED. FOR ALL ELEMENTS WHERE GEOMETRY TEST RESULTS HAVE EXCEEDED TOLERANCES, QUAD4 ELEMENT ID 1 PRODUCED SMALLEST SKEW ANGLE OF 45.00 (TOLERANCE = 60.00).

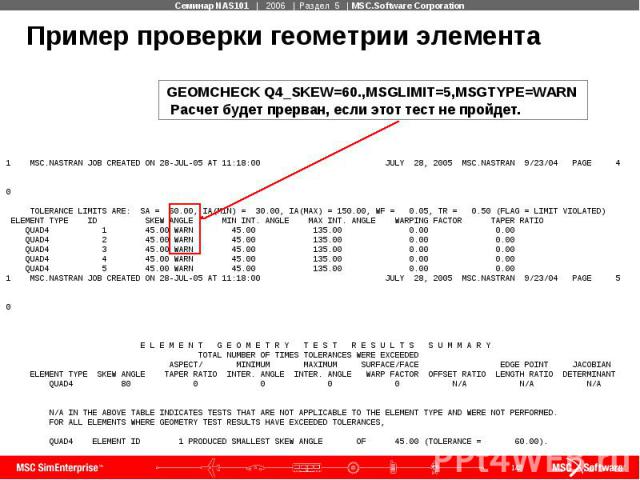
Пример проверки геометрии элемента

Пример проверки геометрии элемента

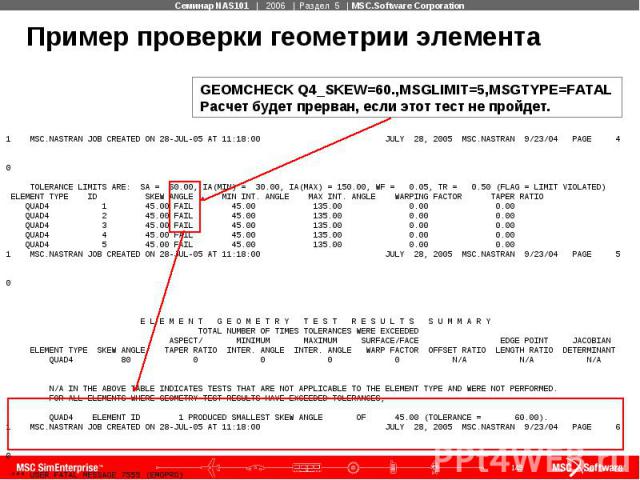
Пример проверки геометрии элемента

Симметрия конструкции Свойства симметрии часто могут использоваться в процессе моделирования для уменьшения ресурсов, требуемых для расчета.

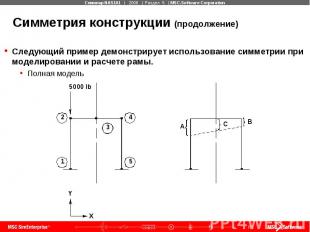
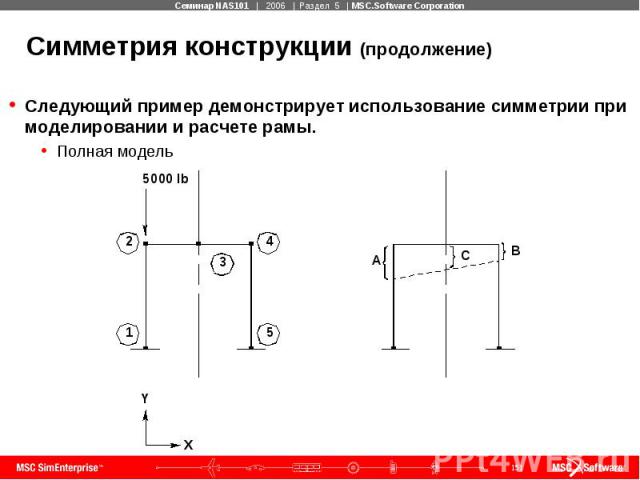
Симметрия конструкции (продолжение) Следующий пример демонстрирует использование симметрии при моделировании и расчете рамы. Полная модель

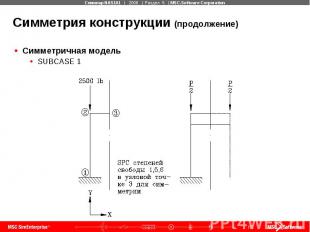
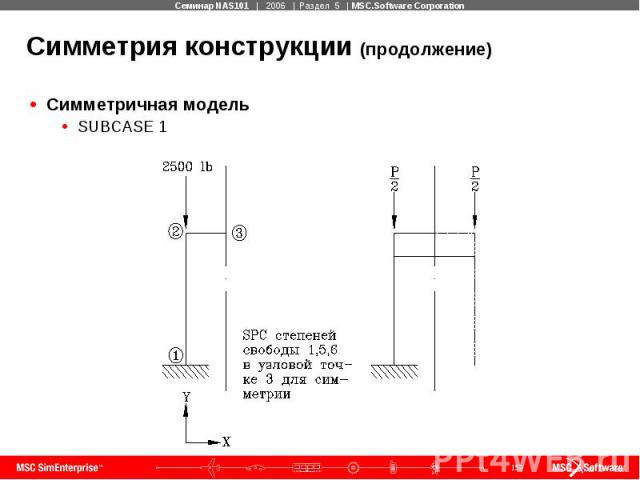
Симметрия конструкции (продолжение) Симметричная модель SUBCASE 1

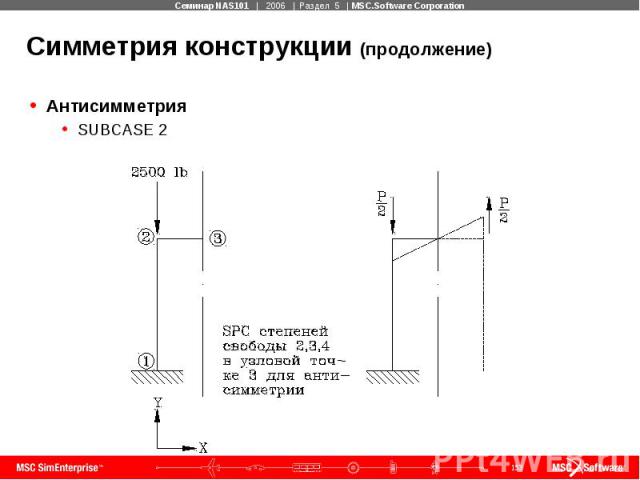
Симметрия конструкции (продолжение) Антисимметрия SUBCASE 2

Симметрия конструкции (продолжение) Входной файл MSC NASTRAN ID SYM,EX TIME 5 SOL 101 CEND $ TITLE =Пример использования условий симметрии/Антисимметрии DISP = ALL $ SUBCASE 1 LABEL = Симметричные ограничения SPC = 1 LOAD = 1 $ SUBCASE 2 LABEL = Антисимметричные ограничения SPC = 2 LOAD = 1 $ SUBCOM 3 LABEL = Левая сторона модели SUBSEQ 1.0, 1.0 $ SUBCOM 4 LABEL = Правая сторона модели SUBSEQ 1.0, -1.0 $ BEGIN BULK $ GRID 1 0.0 0.0 0.0 123456 GRID 2 0.0 10.0 0.0 345 GRID 3 5.0 10.0 0.0 34 $ CBAR 1 100 1 2 -1.0 0.0 0.0 CBAR 2 100 2 3 0.0 1.0 0.0 PBAR 100 1 5.0 5.0 5.0

Симметрия конструкции (продолжение) Входной файл MSC NASTRAN (продолжение) MAT1 1 3.E+7 0.3 $ FORCE 1 2 2500. 0.0 -1.0 0.0 $ SPC1 1 156 3 SPC1 2 2 3 $ ENDDATA

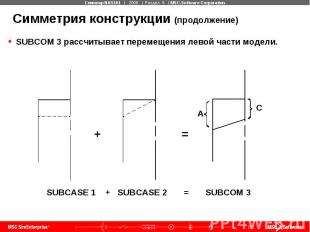
Симметрия конструкции (продолжение)

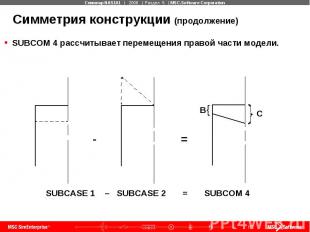
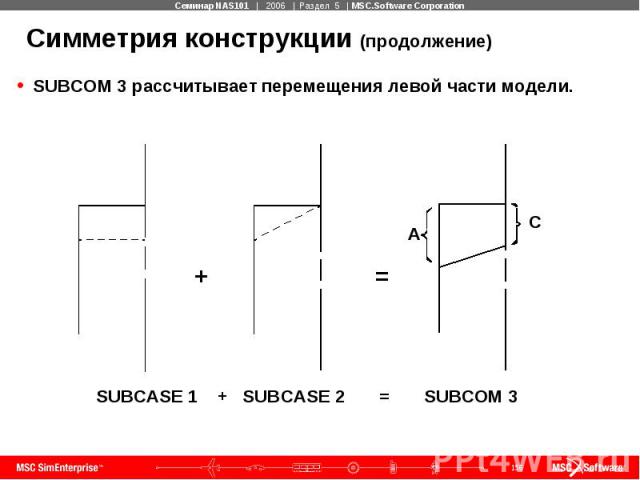
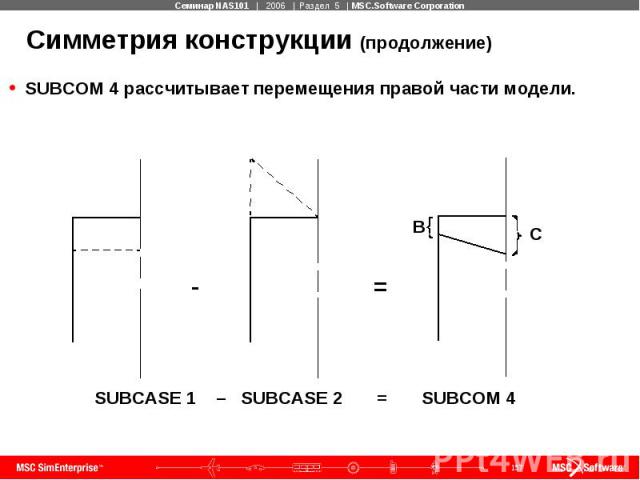
Симметрия конструкции (продолжение) SUBCOM 4 рассчитывает перемещения правой части модели.

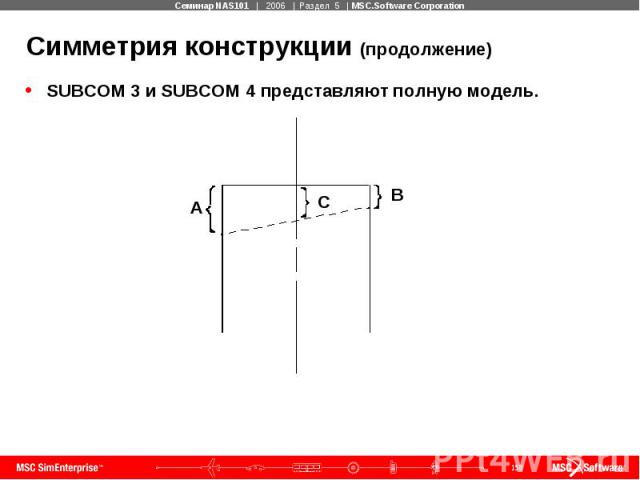
Симметрия конструкции (продолжение) SUBCOM 3 и SUBCOM 4 представляют полную модель.