Презентация на тему: MSC.Nastran 102 2001 - 08

Раздел 8 Анализ частотного отклика

Раздел 8. Анализ частотного оклика ВВЕДЕНИЕ В АНАЛИЗ ЧАСТОТНОГО ОТКЛИКА………………..………………8 - 4 ПЯМОЙ МЕТОД АНАЛИЗА…………….……………………………..……………… 8 - 5 МОДАЛЬНЫЙ МЕТОД АНАЛИЗА…………………………………………………. 8 - 6 ЗАДАНИЕ ВНЕШНЕГО ВОЗДЕЙСТВИЯ…………………………………….……. 8 - 7 ОПЕРАТОР RLOAD……….…………………………………………………………… 8 - 8 ОПЕРАТОР RLOAD2……….………………………………….………………………. 8 - 9 ЗАМЕЧАНИЯ К АНАЛИЗУ ЧАСТОТНОГО ОТКЛИКА...……………….……….. 8 - 10 ОПЕРАТОРЫ FREQi..………………………………………………….……………. 8 - 11 ОПЕРАТОР FREQ.……………………………………………………...……………. 8 - 13 ОПЕРАТОР FREQ1…..…………………………………...…………...………………. 8 - 14 ОПЕРАТОР FREQ2…..………………………………..……………….……………… 8 - 15 ОПЕРАТОР FREQ3..………………………………..……………….………………… 8 - 16 ОПЕРАТОР FREQ4…..…………………………..……………………………………. 8 - 17 ОПЕРАТОР FREQ5……………………………………………………...……………. 8 - 20 МЕТОДЫ ВЫЧИСЛЕНИЯ РЕЗЕЛЬТАТОВ…..……………………...……………. 8 - 22 ПРИМЕНЕНИЕ МОДАЛЬНОГО И ПРЯМОГО МЕТОДОВ…………………..……8 – 23 ФОРМАТЫ ВЫВОДА SORT1 И SORT2……………..………………………………8 - 24

Анализ частотного оклика (продолж.) УПРАВЛЕНИЕ РЕШЕНИЕМ ПРИ АНАЛИЗЕ ЧАСТОТНОГО ОТКЛИКА..….…8 - 25 ВИДЫ ВЫЧИСЛЯЕМЫХ ВЕЛИЧИН.………………………………...……………. 8 - 27 ЧАСТОТНО-ЗАВИСИМЫЕ ПРУЖИНЫ И ДЕМПФЕРЫ..………………………. 8 - 28 ОПЕРАТОР CBUSH.………………………………………...………………………… 8 - 29 ОПЕРАТОР PBUSH……….…………………………………………….………………8 - 32 ОПЕРАТОР PBUSHT….………………………………………………………………. 8 - 34 ПРИМЕР ЧАСТОТНО-ЗАВИСИМОГО ИМПЕДАНСА…………………………… 8 - 36 ПРИМЕР ИСПОЛЬЗОВАНИЯ ЭЛЕМЕНТА CBUSH…………………….…………8 - 37 РЕЗУЛЬТАТЫ РАСЧЕТА ПЕРЕМЕЩЕНИЙ ДЛЯ ЭЛЕМЕНТА CBUSH ..……..8 - 38 РЕЗУЛЬТАТЫ РАСЧЕТА СИЛ ДЛЯ ЭЛЕМЕНТА CBUSH ….……………..……8 - 39 ПРИМЕР №5 – АНАЛИЗ ЧАСТОТНОГО ОТКЛИКА ПРЯМЫМ МЕТОДОМ.…8 - 40 ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №5.……………………………….……….. 8 - 42 РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №5….…………………………..…….. 8 - 43 ПРИМЕР №6 – АНАЛИЗ ЧАСТОТНОГО ОТКЛИКА МОДАЛЬНЫМ МЕТОДОМ…………………………………………………………… 8 - 48 ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №6….…………………………….………. 8 - 50 РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №6……….…………………………… 8 - 52

Введение в анализ частотного отклика Вычисление отклика на гармоническое воздействие. Воздействие в явной форме определено в частотной области – величины всех прилагаемых силовых факторов известны на всех частотах. Обычно вычисляются узловые перемещения, а также силы и напряжения в элементах. Результаты решения – комплексные величины: амплитуда и фаза (относительно воздействия) или действительная и мнимая часть отклика. Два типа анализа – прямой и модальный.

Прямой метод анализа Уравнение колебаний: (1) Параметры PARAM,G и GE в операторе MATi формируют не матрицу демпфирования, а комплексную матрицу жесткости (2) где K1 – глобальная матрица жесткости G – коэффициент глобального конструкционного демпфирования (PARAM,G) KE – матрица жесткости элемента GE – коэффициент конструкционного демпфирования элемента (параметр GE в операторе MATi) Сравните с анализом переходного процесса Выражение (2) подставляется в уравнение (1), а затем оно решается аналогично статической задаче (с использованием комплексной арифметики).

Модальный метод анализа Физические координаты конвертируются в модальные, а затем анализируются несвязанные системы с одной степенью свободы (СС) Решение выполняется много быстрее, чем прямым методом Уравнения несвязанные, если присутствует только модальное демпфирование (задаваемое оператором TABDMP1) или его нет совсем . В противном случае, если есть немодальное демпфирование (элементы VISC, DAMP), то для решения используется менее эффективный прямой подход (однако, все же, на небольших модальных матрицах).

Задание внешнего воздействия Внешнее воздействие задается как функция частоты. В MSC.Nastran предусматриваются различные методы: RLOAD1 (задание воздействия в виде действительной и мнимой компонент) RLOAD2 (задание воздействия в форме амплитуды и фазы) LSEQ (конвертация статических нагрузок в динамические) Оператор DLOAD в Bulk Data Section используется для комбинирования частотно-зависимых нагрузок. Операторы RLOADi инициируются оператором DLOAD в Case Control Section.


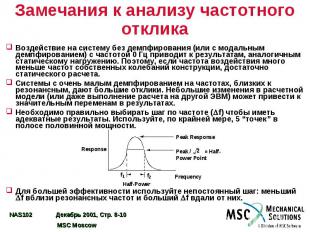
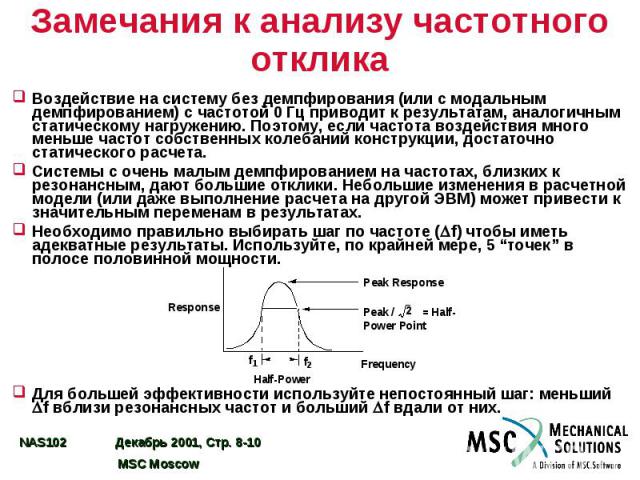
Замечания к анализу частотного отклика Воздействие на систему без демпфирования (или с модальным демпфированием) с частотой 0 Гц приводит к результатам, аналогичным статическому нагружению. Поэтому, если частота воздействия много меньше частот собственных колебаний конструкции, достаточно статического расчета. Системы с очень малым демпфированием на частотах, близких к резонансным, дают большие отклики. Небольшие изменения в расчетной модели (или даже выполнение расчета на другой ЭВМ) может привести к значительным переменам в результатах. Необходимо правильно выбирать шаг по частоте ( f) чтобы иметь адекватные результаты. Используйте, по крайней мере, 5 “точек” в полосе половинной мощности. Для большей эффективности используйте непостоянный шаг: меньший f вблизи резонансных частот и больший f вдали от них.

Операторы FREQi Задают шаг по частоте. Оператор FREQ задает дискретные значения частот воздействия. Оператор FREQ1 задает начальное значение частоты, инкремент (шаг) и число инкрементов (шагов). Оператор FREQ2 задает начальное и конечное значения частоты, а также количество логарифмических интервалов. Оператор FREQ3 задает частоты F1, F2 и количество частот воздействия между F1, собственными частотам конструкции и F2. Допускает неравномерную разбивку интервалов. Оператор FREQ4 задает частоты F1 и F2, частотный диапазон и количество частот воздействия “около” каждой из собственных частот конструкции, “попадающих” в диапазон (F1,F2). Оператор FREQ5 задает частоты F1 и F2 и доли собственных частот конструкции, на которых будет вычисляться воздействие, если они (вычисленные частоты) находятся в диапазоне (F1,F2). Операторы FREQ3, FREQ4 и FREQ5 применимы только при модальном методе анализа.

Операторы FREQi Операторы FREQi вBulk Data Section инициируются оператором FREQUENCY в Case Control Section. Все операторы FREQi в Bulk Data Section, имеющие одинаковый идентификатор, инициируются одним оператором FREQUENCY в Case Control Section. Следовательно, операторы FREQ, FREQ1, FREQ2, FREQ3, FREQ4 и FREQ5 могут использоваться одновременно.






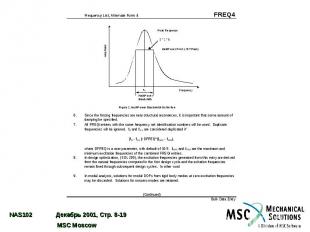



Методы вычисления результатов Предусмотрены два метода вычисления результатов при модальном анализе: метод модальных перемещений и матричный метод. где H – количество мод F – количество частот воздействия Матричный метод задан “по умолчанию”, он менее затратен при H < F и рекомендуется к применению в большинстве случаев. Метод модальных перемещений может быть инициирован с помощью параметра PARAM,DDRMM,-1.

Применение модального и прямого методов

Форматы вывода SORT1 и SORT2 SORT1: для частоты воздействия выводятся результаты по всем узлам и элементам, затем для другой частоты и т.д. SORT2: для узла (элемента) выводятся результаты по всем частотам, затем для другого узла (элемента) и т.д. Рекомендации по использованию Если указана “смесь” форматов SORT1 и SORT2, то “по умолчанию”при анализе частотного отклика будет использован SORT1, а переходного процесса - SORT2.

Управление решением при анализе частотного отклика Executive Control Section SOL <см. таблицу> Case Control Section DLOAD (требуется при обоих методах решения) LOADSET (может применяться при обоих методах) METHOD (требуется при модальном методе) SDAMPING (может применяться при модальном методе) FREQUENCY (требуется при обоих методах решения)

Управление решением при анализе частотного отклика Bulk Data Section ASET,OMIT (может применяться при обоих методах) EIGRL or EIGR (требуется при модальном методе) FREQ (требуется при обоих методах решения) RLOADi (требуется при обоих методах решения) LSEQ (может применяться при обоих методах) DAREA (требуется при обоих методах решения*) DELAY (может применяться при обоих методах) DPHASE (может применяться при обоих методах) TABDMP1 (может применяться при модальном методе) DLOAD (может применяться при обоих методах) *Идентификатор оператора DAREA необходим; если же применяется оператор LSEQ, то сам оператор DAREA может отсутствовать.

Виды вычисляемых величин Результаты вычислений для узлов ACCELERATION DISPLACEMENT (или VECTOR) OLOAD SACCELERATION SDISPLACEMENT SVELOCITY SVECTOR SPCFORCES VELOCITY MPCFORCE Результаты вычислений для элементов ELSTRESS (или STRESS) ELFORCE (или FORCE) STRAIN ESE EKE EDE Специальный оператор OFREQUENCY (задание частот, для которых должны выводиться результаты; работает совместно с оператором FREQUENCY)

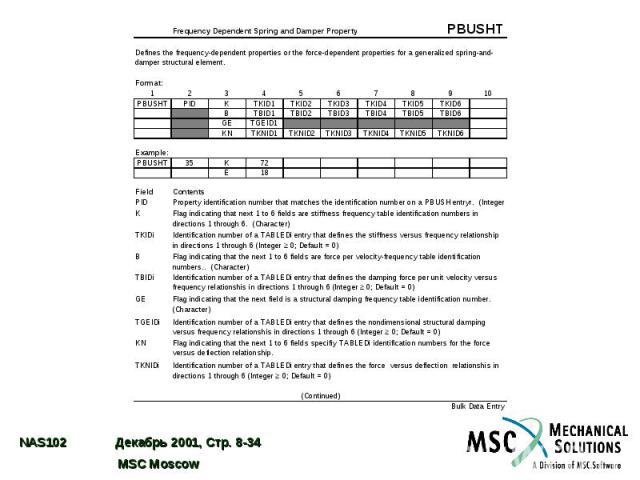
Частотно-зависимые пружины и демпферы Жесткость зависит от частоты воздействия Демпфирование зависит от частоты воздействия Различный импеданс в различных направлениях Оператор CBUSH Задание топологии элемента Оператор PBUSH Задание основных свойств элемента (не частотно-зависимых) Оператор PBUSHT Задание частотно-зависимых свойств элемента







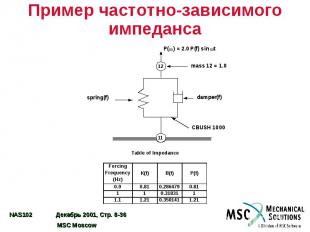
Пример частотно-зависимого импеданса

Пример использования элемента CBUSH

Результаты расчета перемещений для элемента CBUSH

Результаты расчета сил для элемента CBUSH

Пример №5 Анализ частотного отклика прямым методом

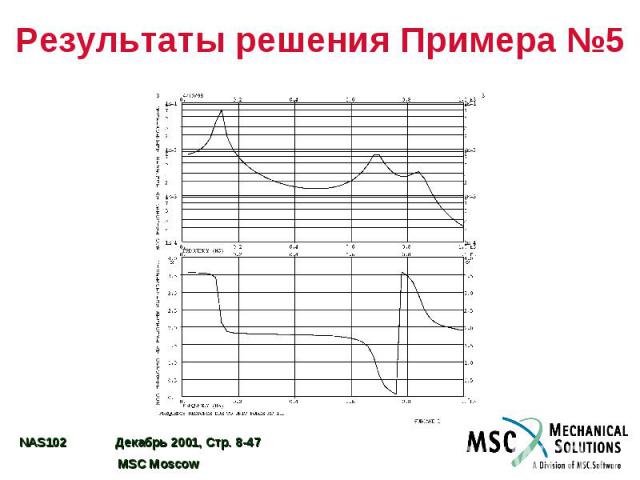
Пример №5. Анализ частотного отклика прямым методом Используя модель из Примера №1, прямым методом определите частотный отклик плоской пластины под действием гармонического возмущения – сосредоточенной силы, действующей на угол пластины. Определить решение с шагом 20 Гц в диапазоне 20 – 1000 Гц. Использовать конструкционное демпфирование g=0,06.

Входной файл для Примера №5

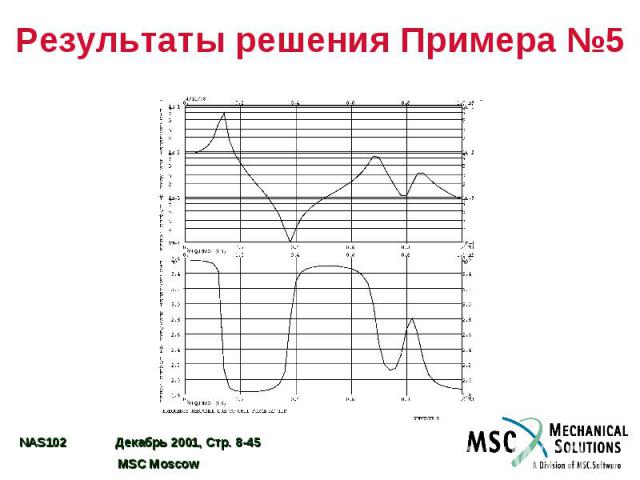
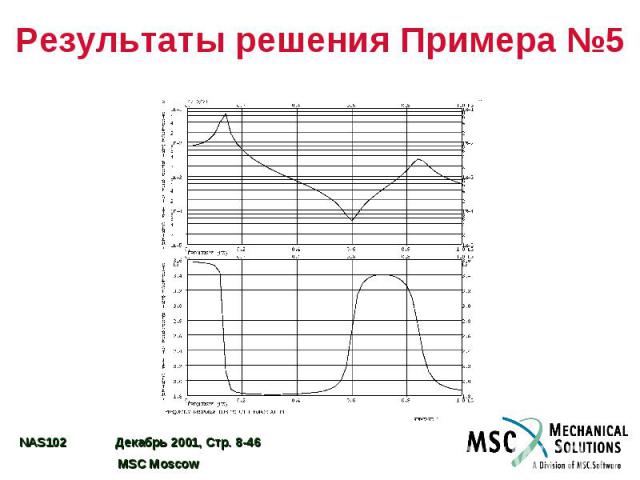
Результаты решения Примера №5

Результаты решения Примера №5
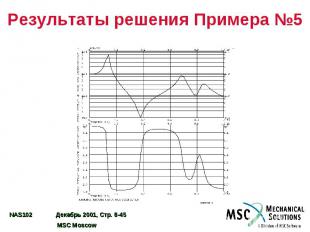
Результаты решения Примера №5
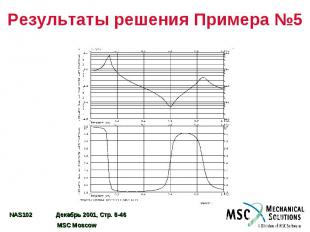
Результаты решения Примера №5
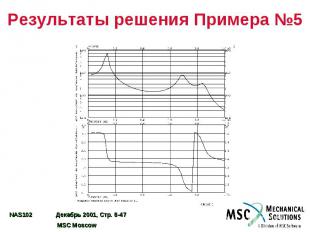
Результаты решения Примера №5

Пример №6 Анализ частотного отклика модальным методом

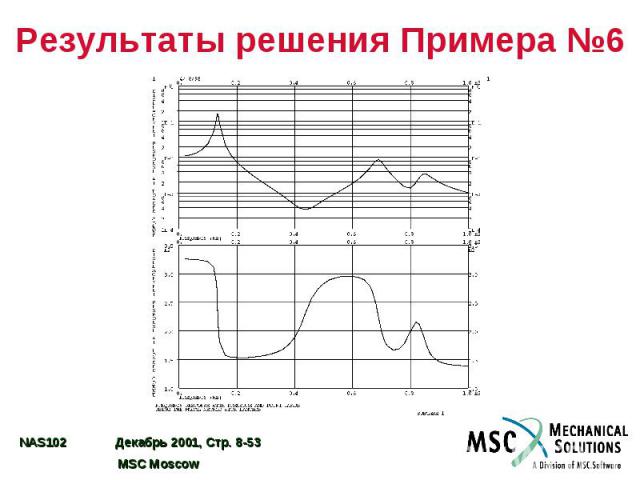
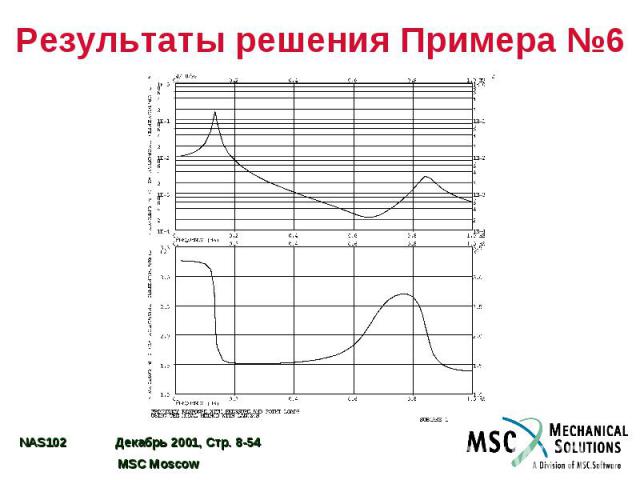
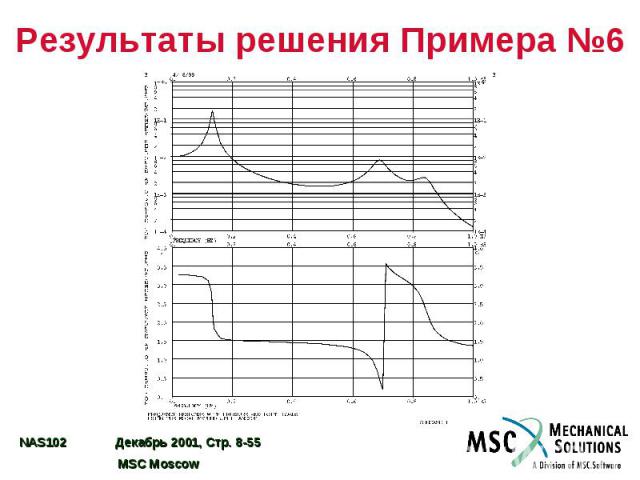
Пример №6. Анализ частотного отклика модальным методом Используя модель из Примера №1, модальным методом определите частотный отклик плоской пластины под действием гармонического возмущения – давления в 0,1 фунт/кв. дюйм и сосредоточенной силы в 1 фунт, приложенной к углу пластины и запаздывающей по фазе на 45o. Использовать модальное демпфирование = 0,03. Определить решение с шагом 20 Гц в диапазоне 20 – 1000 Гц, а также на пяти частотах в диапазоне половинной мощности вблизи каждой резонансной частоты конструкции.

Входной файл для Примера №6

Входной файл для Примера №6

Результаты решения Примера №6
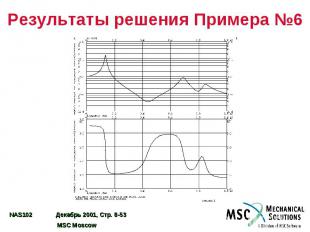
Результаты решения Примера №6
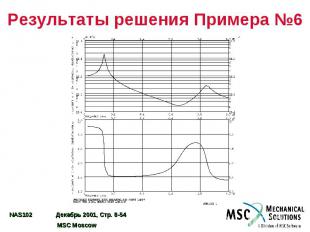
Результаты решения Примера №6
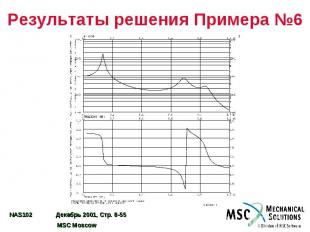
Результаты решения Примера №6