Презентация на тему: MSC.Nastran 102 2001 - 04

Раздел 4 Редуцирование в динамическом анализе

Раздел 4. Редуцирование в динамическом анализе ВВЕДЕНИЕ В ДИНАМИЧЕСКОЕ РЕДУЦИРОВАНИЕ………………………………….… 4 - 3 МЕТОДЫ ДИНАМИЧЕСКОГО РЕДУЦИРОВАНИЯ В MSC.Nastran…………………… 4 - 4 СТАТИЧЕСКАЯ КОНДЕНСАЦИЯ (ВНУТРЕНЕЕ ВЫЧИСЛЕНИЕ)...…………………… 4 - 5 ИНТЕРФЕЙС ПОЛЬЗОВАТЕЛЯ.……………………………………………………………. 4 - 9 УПРАВЛЕНИЕ ЕШЕНИЕМ ПРИ РЕДУЦИРОВАНИИ ГАЙАНА.………………………. 4 - 10 ПРОБЛЕМЫ, ВОЗНИКАЮЩИЕ ПРИ РЕДУЦИРОВАНИИ ГАЙАНА..………………. 4 - 11 МОДАЛЬНОЕ РЕДУЦИРОВАНИЕ………………………………………………………… 4 - 13 УПРАВЛЕНИЕ РЕШЕНИЕМ ПРИ МОДАЛЬНОМ РЕДУЦИРОВАНИИ……………… 4 - 15 ПРИМЕР №2 – МОДАЛЬНЫЙ АНАЛИЗ С ИСПОЛЬЗОВАНИЕМ РЕДУЦИРОВАНИЯ ГАЙАНА..………………………………………………………….….. 4 - 16 ПРИМЕР №2 – МОДАЛЬНЫЙ АНАЛИЗ ПЛОСКОЙ ПЛАСТИНЫ С ИСПОЛЬЗОВАНИЕМ СТАТИЧЕСКОГО РЕДУЦИРОВАНИЯ……………..………….. 4 - 17 ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №2..………………………………………………….. 4 - 19 РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №2……..………………………………………… 4 - 20

Введение в динамическое редуцирование Определение Динамическое редуцирование – это преобразование одной динамической математической модели в другую с меньшим количеством степеней свободы. Причины применения динамического редуцирования Математическая модель м.б. слишком велика для того, чтобы использовать ее без редуцирования. Математическая модель может быть излишне подробной. Динамическое редуцирование позволяет исключить отдельные локальные моды. Применение динамического редуцирования дает большую точность (и, вероятно, дешевле), чем создание отдельной, более компактной модели.

Методы динамического редуцирования в MSC.Nastran Редуцирование Гайана (Guyan) – статическая конденсация Обобщенное динамическое редуцирование (GDR, см. Приложение A) Модальное редуцирование Синтез модальных компонентов (component mode synthesis) – разновидность метода суперэлементов – см. Раздел 16.

Статическая конденсация (внутреннее вычисление) Положим, что {uf} – набор незакрепленных (свободных) координат конструкции. Разделим где ua – набор анализируемых координат (analysis set) uo – набор неучитываемых координат (omitted set)

Статическая конденсация (внутреннее вычисление) Запишем статическое уравнение для uf и разделим матрицу жесткости на O-set и the A-set. Предположим Po равным нулю и решим уравнение, выразив uo через ua Переход от A-set к F-set запишется как Зависимость O-set от A-set выражается уравнением (2): O-set – линейная комбинация компонентов A-set, причем столбцы Goa – векторы статической деформации конструкции.

Статическая конденсация (внутреннее вычисление) Уравнения для F-set записываются через A-set Динамические задачи решаются относительно редуцированных “координат” (A-set). Компоненты O-set вычисляются с помощью уравнения (2). Массы, демпфирование и жесткости, ассоциирующиеся с O-set, “размазываются” на A-set. Наибольшие затраты ассоциируются с формированием матриц Maa и Baa, особенно недиагональной матрицы Mff (при распределенной формулировке массы). Полученные в результате матрицы Kaa, Baa и Maa - небольшие и плотно заполненные (ленточная структура матриц нарушается).

Статическая конденсация (внутреннее вычисление) МЕТОДИКА ПРИМЕНЕНИЯ Разделяйте степени свободы (Uf) на O-set (U0) и A-set (UA) с помощью операторов OMIT или ASET. Сохраняйте только малую часть степеней свободы (обычно 10% или меньше) в A-set, т.к. вычислительные затраты на статическую конденсацию быстро растут с увеличением величины A-set. Или же сохраняйте в A-set все СС . Сохраняйте СС с большими сосредоточенными массами в A-set. Сохраняйте в A-set СС, к которым “прикладываются” нагрузки (в анализе переходного процесса и частотного отклика). Сохраняйте в A-set СС, необходимые для адекватного описания форм колебаний, представляющих интерес.

Интерфейс пользователя Либо и/или или OMIT, OMIT1 Указывайте либо A-set (с помощью оператора ASET), либо O-set (с помощью оператора OMIT). Неуказанные степени свободы автоматически относятся к противоположному набору СС.

Управление решением при редуцировании Гайана Executive Control Section Любой оператор SOL Case Control Section Не требуется специальных команд Bulk Data Section ASET* (спецификация A-set) OMIT* (спецификация O-set) *Неуказанные степени свободы автоматически относятся к противоположному набору СС. Если специфицированы оба набора (ASET и OMIT), то неуказанные компоненты относятся к O-set.

Проблемы, возникающие при редуцировании Гайана Пользователь должен сформировать A-set Точность зависит от умения пользователя сформировать A-set Независимо от навыков пользователя для высокой точности расчетов необходима большая размерность A-set – не менее, чем в 2-5 раз больше, чем желаемое количество сохраняемых форм колебаний Редуцирование жесткости выполняется точно, масс и демпфирования – только приближенно Наибольшие погрешности имеют место при моделировании “высоких” мод колебаний Локальные моды могут быть “потеряны” вовсе РЕЗЮМЕ В целом не рекомендуется к применению, за исключением анализа согласованности результатов расчетов и испытаний (см. Раздел 20)

Проблемы, возникающие при редуцировании Гайана При статической конденсации локальные динамические эффекты могут быть “потеряны”.

Модальное редуцирование Все типы линейных динамических решений в MSC.Nastran имеют две разновидности. Прямое решение – решение относительно компонентов A-set. Модальное решение – решение относительно модальных координат (H-set). В модальных алгоритмах координаты A-set записываются через модальные координаты. Модальные векторы (модальные формы) – это результат решения собственной задачи без учета демпфирования (в A-set координатах)

Модальное редуцирование Уравнения колебаний для A-set записываются относительно модальных координат (H-set notation), причем это выполняется автоматически. (Замечание: E-set не показан для компактности записи) Если собственные векторы нормализованы по массе и не используются K2PP, M2PP, B2PP и TF, тогда: Замечание: матрицы A-set м.б. результатом редуцирования Гайана или GDR. В этом случае трансформирование из модальных координат в F-set потребует двух преобразований.

Управление решением при модальном редуцировании Executive Control Section Любой (динамический) оператор SOL Case Control Section METHOD (инициализирует операторы EIGR или EIGRL в Bulk Data Section) Bulk Data Section EIGR или EIGRL (задаются параметры решения собственной задачи)

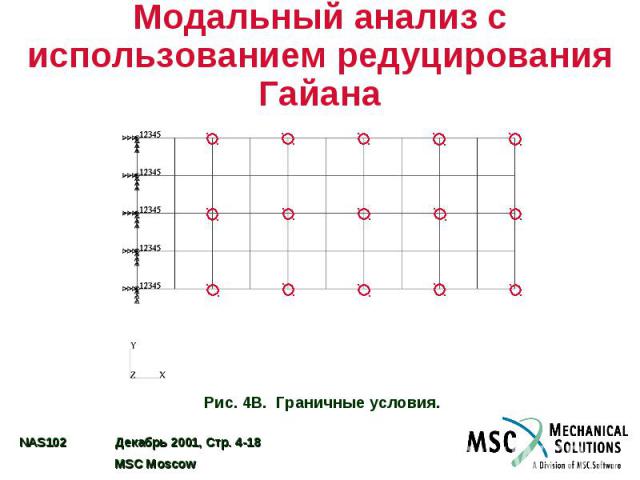
Пример №2 Модальный анализ с использованием редуцирования Гайана

Пример №2. Модальный анализ с использованием редуцирования Гайана Используя метод Гайана, редуцировать модель, применявшуюся в Примере №1. Используя автоматический метод Хаусхольдера, найти первые пять собственных частот. Для A-set использовать узлы, указанные на рисунке 4B. Рис. 4A. Координаты узлов и топология элементов.

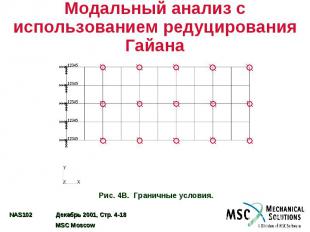
Модальный анализ с использованием редуцирования Гайана Рис. 4B. Граничные условия.

Входной файл для Примера №2

Результаты решения для Примера №2