Презентация на тему: MSC.Nastran 102 2001 - 06

Раздел 6 Демпфирование

Раздел 6. Демпфирование ДЕМПФИРОВАНИЕ…………………………………………………………………………… 6 - 3 КОНСТРУКЦИОННОЕ И ВЯЗКОЕ ДЕМПФИРОВАНИЕ………………………………… 6 - 4 КОНСТРУКЦИОННОЕ И ВЯЗКОЕ ДЕМПФИРОВАНИЕ (ПОСТОЯННЫЕ ПЕРЕМЕЩЕНИЯ)..………………………………………………. 6 - 7 ДЕМПФИРОВАНИЕ (ВЫВОДЫ)..………………………………………………………….. 6 - 8 КОНСТРУКЦИОННОЕ ДЕМПФИРОВАНИЕ.……………………………………………… 6 - 9 ВЯЗКОЕ ДЕМПФИРОВАНИЕ.……………………………………………………………… 6 - 10 МОДАЛЬНОЕ ДЕМПФИРОВАНИЕ………………………………………………………… 6 - 18 ДЕМПФИРОВАНИЕ РЭЛЕЯ.……………………………………………………………….. 6 - 19

Демпфирование Демпфирование – это рассеивание энергии, наблюдающееся в конструкциях. Точное моделирование демпфирования затруднено вследствие множественности механизмов его возникновения: Вязкостные эффекты (буфер, амортизатор) Внешнее трение (трение в соединениях конструкции) Внутреннее трение (характерная особенность материала) Структурные нелинейности (пластичность) Аналитические зависимости, использующиеся для моделирования демпфирования Вязкая демпфирующая сила Конструкционная демпфирующая сила

Конструкционное и вязкое демпфирование Предположим, что колебания синусоидальные: Тогда: Вязкое демпфирование: Конструкционное демпфирование:

Конструкционное и вязкое демпфирование Уравнения идентичны, если: Следовательно, если конструкционное демпфирование (g) моделируется эквивалентным вязким демпфированием (b), то указанное уравнение справедливо только на одной частоте w3 (или w4). если но

Конструкционное и вязкое демпфирование тогда - коэффициент апериодичности (доля критического демпфирования) g = - коэффициент конструкционного демпфирования Q – добротность (или динамический фактор)
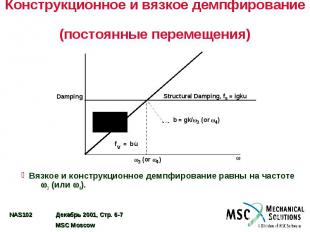
Конструкционное и вязкое демпфирование (постоянные перемещения) Вязкое и конструкционное демпфирование равны на частоте 3 (или 4).

Демпфирование (выводы) Вязкая демпфирующая сила пропорциональна скорости Конструкционная демпфирующая сила пропорциональна перемещению (деформации) Коэффициент апериодичности Коэффициент добротности Q обратно пропорционален величине энергии, рассеивающейся за один цикл колебаний При резонансе = g/2 Q = 1/(2 ) Q = 1/g

Конструкционное демпфирование Конструкционное демпфирование Операторы MATi PARAM,G, <коэффициент> (по умолчанию = 0) Коэффициент глобального конструкционного демпфирования (умножается на глобальную матрицу жесткости системы) PARAM,W3, <коэффициент> (по умолчанию = 0) Конвертирует глобальное конструкционное демпфирование в эквивалентное вязкое демпфирование PARAM,W4, <коэффициент> (по умолчанию = 0) Конвертирует конструкционное демпфирование в элементе в эквивалентное вязкое демпфирование Единицы измерения W3 и W4 – рад/ед. времени Если используется PARAM,G, <…>, то <коэффициент> в операторе PARAM,W3, … д.б. больше нуля, иначе оператор PARAM,G при анализе переходного процесса будет игнорирован (подробнее см. Раздел 7).

Вязкое демпфирование Скалярное вязкое демпфирование

Вязкое демпфирование

Вязкое демпфирование

Вязкое демпфирование

Вязкое демпфирование

Вязкое демпфирование

Вязкое демпфирование

Вязкое демпфирование

Модальное демпфирование CASE CONTROL SDAMP = n $ “инициализирует” таблицу модального демпфирования. BULK DATA TABDMP1,n,CRIT ,x1,y1,x2,y2,..endt $ Зависимость демпфирования ("G", "CRIT" или "Q") $ от частоты.

Демпфирование Рэлея Пропорционально матрице массе и/или матрице жесткости Известно также как “пропорциональное” демпфирование Пропорциональность матрице масс PARAM,ALPHA1,<x> Пропорциональность матрице жесткости PARAM,ALPHA2,<y> Применимо при анализе переходного процесса и анализе частотного отклика Коэффициенты умножаются на матрицы, соответствующие наборам степеней свободы d-set (при прямом анализе) или h-set (при модальном анализе) “Добавка” к матрице вязкого демпфирования: [B’] = [B] + {alpha1 * [M] + alpha2 * [K]}

Демпфирование Рэлея ALPHA1 и ALPHA2 – комплексные параметры, например PARAM, ALPHA2, 1.25E-4, 0. Интерпретация модальной матрицы демпфирования