Презентация на тему: MSC.Nastran 102 2001 - 17

Раздел 17 Внешние переменные, передаточные функции и элементы NOLIN

Раздел 17. Внешние переменные, передаточные функции и элементы NOLIN ВНЕШНИЕ ПЕРЕМЕННЫЕ..………………………………….………………………17 - 3 ПЕРЕДАТОЧНЫЕ ФУНКЦИИ...………………………………………..……………. 17 - 4 НЕЛИНЕЙНЫЕ СИЛОВЫЕ ФАКТОРЫ.……………………………………..…… 17 - 5 ОСОБЕННОСТИ ИСПОЛЬЗОВАНИЯ НЕЛИНЕЙНЫХ СИЛ………………….. 17 - 7 ЭЛЕМЕНТЫ NOLIN...………………………………………………….……………… 17 - 8 ПРИМЕР №13 – ЛИНЕЙНЫЙ АНАЛИЗ ПЕРЕХОДНОГО ПРОЦЕССА С ИСПОЛЬЗОВАНИЕМ ЭЛЕМЕНТОВ NOLIN…………………………………… 17 - 10 ПРИМЕР №13 – ПЕРЕЕЗД АВТОМОБИЛЯ ЧЕРЕЗ НЕРОВНОСТЬ………… 17 - 11 ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №13..………………………….……………… 17 - 13 РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №13.………………………………...……. 17 - 15

Внешние переменные Степени свободы, не связанные с конструкцией используются для представления не связанных с конструкцией переменных. Задаются оператором EPOINT в Bulk Data Section. Могут использоваться только в остаточной структуре для динамического анализа (E-set - часть набора D-set). Неподвержены никаким процедурам редуцирования, включая модальное редуцирование. Не могут использоваться как конструкционные СС. Не могут быть “связаны” (закреплены) посредством MPC или SPC. Могут использоваться только в матрицах прямого ввода типа P и в передаточных функциях. Могут подвергаться динамическому нагружению только посредством оператора DAREA в Bulk Data Section.

Передаточные функции Передаточные функции (ПФ) используются для задания динамических связей в форме: где ud - зависимая переменная u - независимая переменная p - оператор дифференцирования (p = d/dt) Эквивалентны матрицам типа P, вводимым оператором DMIG (M2PP, B2PP, K2PP) ПФ складываются с другими матрицами типа P. ud определяет строку матрицы, к элементам которой будут добавлены коэффициенты b0, b1, b2. ui определяет столбец, к элементам которого будут добавлены коэффициенты a0, a1, и a2. Задаются оператором TF в Bulk Data Section, который инициируется оператором TFL в Case Control Section.

Нелинейные силовые факторы Нелинейные силовые факторы, прикладываемые к узлам N(t) – нелинейная сила (момент), являющаяся функцией перемещения или скорости. Задаются операторами NOLINi в Bulk Data Section, инициируемыми оператором NONLINEAR Case Control Section. Применяются только при анализе переходного процесса (должны прикладываться к переменным E-set при модальном методе решения или к переменным D-set при прямом методе решения).

Нелинейные силовые факторы Нелинейные силы представляют отклонения от линейных зависимостей. Наиболее просто используется при прямом методе решения: нелинейная сила просто прикладывается к узлу. Модальный метод предполагает использование внешних переменных и передаточных функций, т.к. при модальной формулировке только к переменным E-set могут прикладываться нелинейные силы.

Особенности использования нелинейных сил Нелинейные силы вычисляются по результатам, полученным на предыдущем шаге. Меньшее значение t позволит получить большую точность. Нелинейные силы м.б. приложены только к переменным D-set (A-set + E-set) при прямом методе и H-set (modal set + E-set) при модальном методе. СС, к которым прикладываются нелинейные силы, не могут быть в наборе O-set, так же как и быть зависимыми. При приложении сил по направлениям, не совпадающим с направлениями глобальной системы координат, необходимо использовать локальные системы координат. Отладьте эти приемы на “пилотной” модели.

Элементы NOLINS NOLIN1 – нелинейная сила в форме таблицы Функция перемещения Функция скорости NOLIN2 – нелинейная сила в форме “произведения” двух таблиц где Xj и Xk могут быть значениями двух перемещений или же двумя значениями одного и того же перемещения

Элементы NOLINS NOLIN3 – нелинейная сила в форме экспоненциальной функции положительного аргумента где Xj может быть как перемещением, так и скоростью NOLIN4 - нелинейная сила в форме отрицательного значения экспоненциальной функции отрицательного аргумента где Xj может быть как перемещением, так и скоростью

Пример №13 Нелинейный анализ переходного процесса с использованием элементов NOLIN
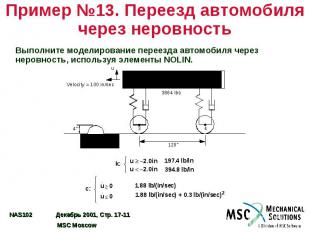
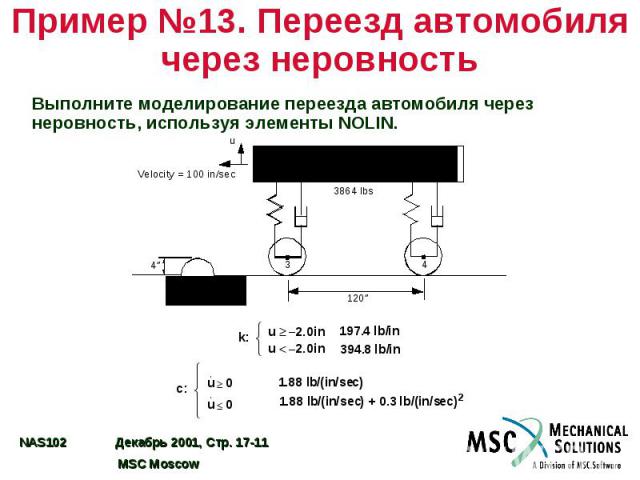
Пример №13. Переезд автомобиля через неровность Выполните моделирование переезда автомобиля через неровность, используя элементы NOLIN.

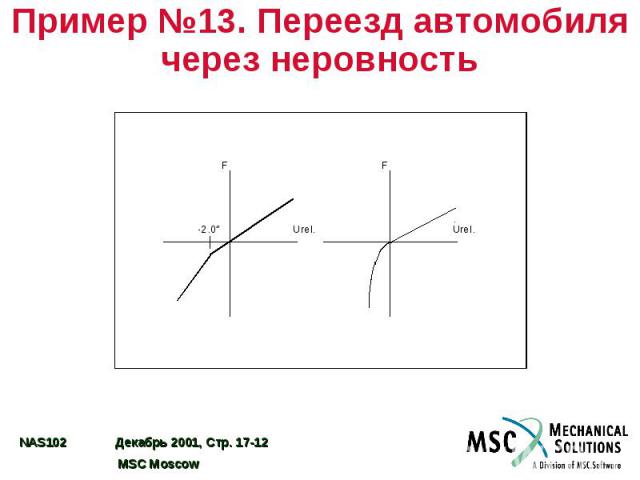
Пример №13. Переезд автомобиля через неровность

Входной файл для Примера №13

Входной файл для Примера №13

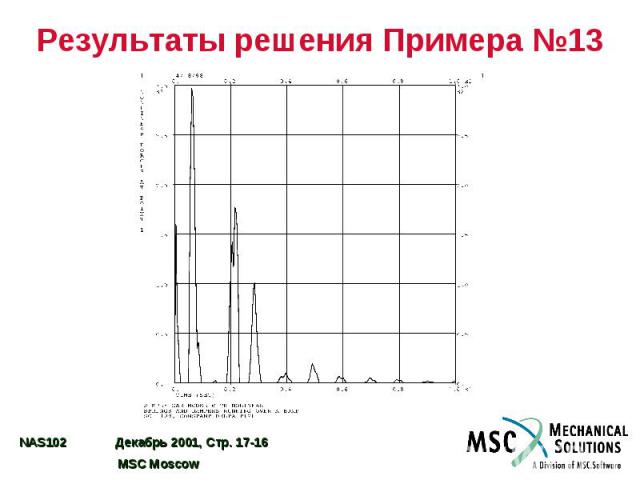
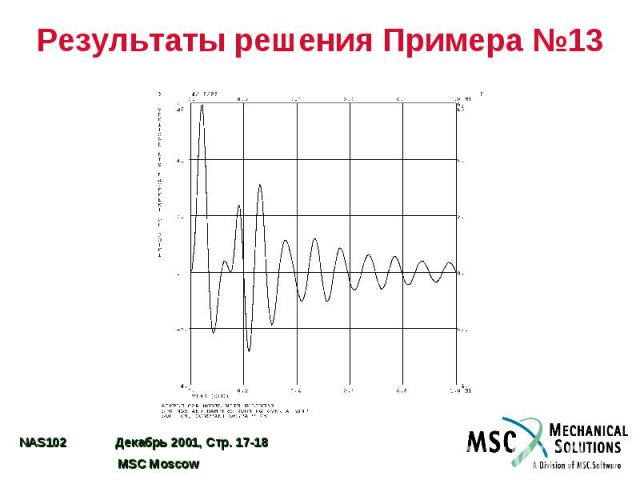
Результаты решения Примера №13
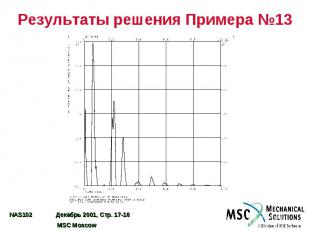
Результаты решения Примера №13
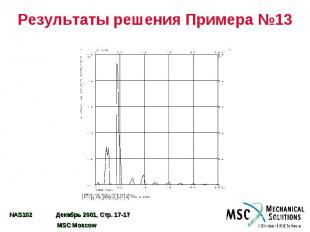
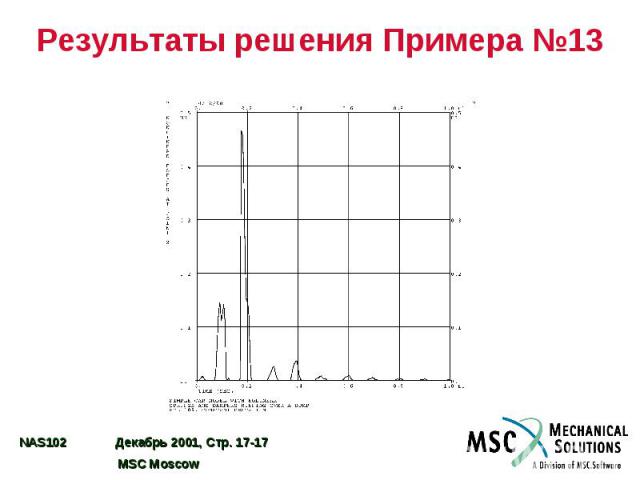
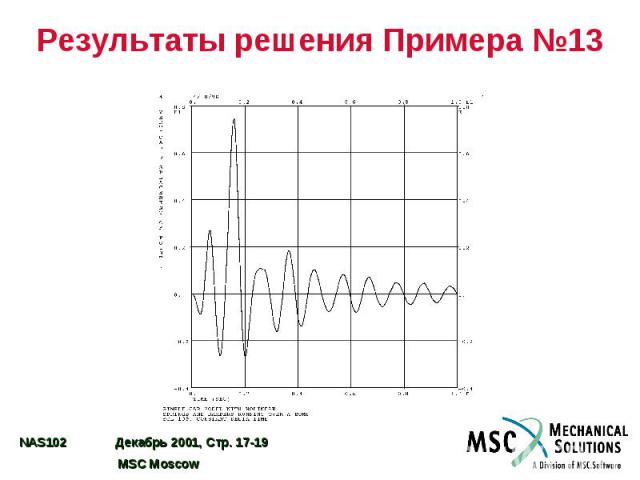
Результаты решения Примера №13
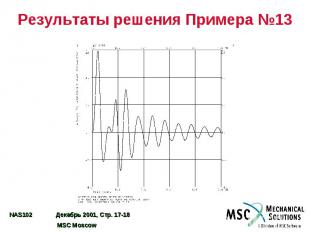
Результаты решения Примера №13
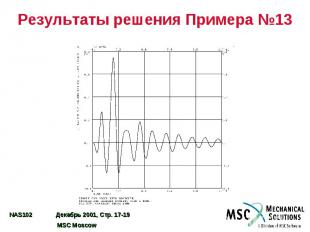
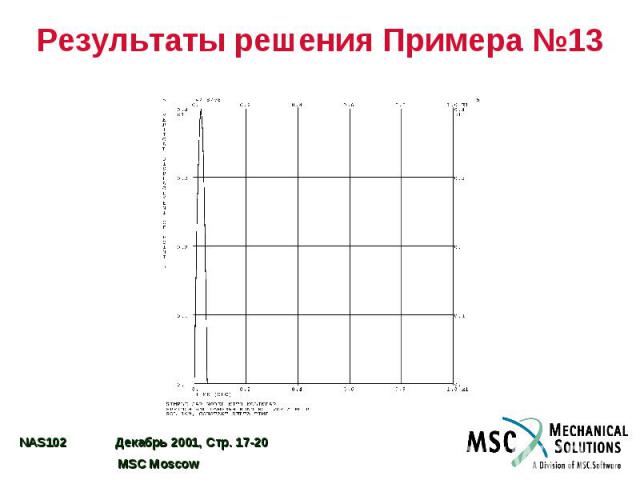
Результаты решения Примера №13

Результаты решения Примера №13

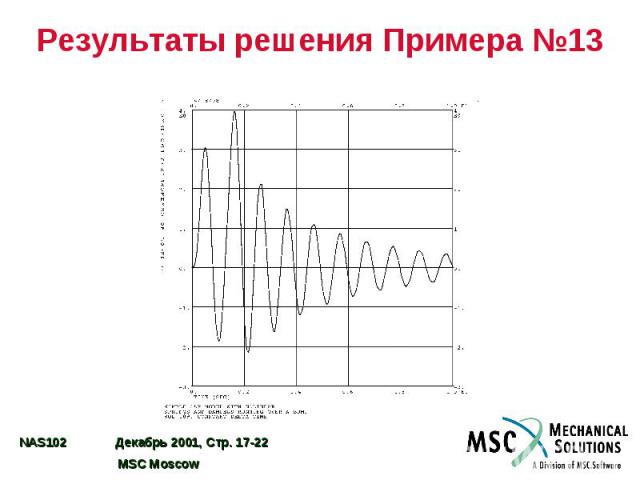
Результаты решения Примера №13
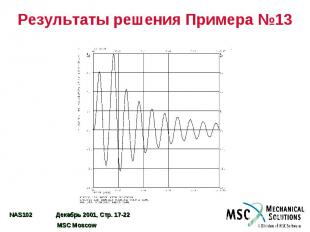
Результаты решения Примера №13