Презентация на тему: MSC.Nastran 102 2001 - 14

Раздел 14 Анализ отклика на случайное воздействие

Раздел 14. Анализ отклика на случайное воздействие ТИПЫ ДИНАМИЧЕСКИХ ПРОЦЕССОВ………………………………… 14 - 4 АНАЛИЗ ОТКЛИКА НА СЛУЧАЙНОЕ ВОЗДЕЙСТВИЕ..……...…….. 14 - 5 ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ......……………………………… 14 - 6 ПРИМЕРЫ СЛУЧАЙНЫХ ПРОЦЕССОВ………………..……………… 14 - 7 ПРИМЕР АНСАМБЛЯ ЭРГОДИЧЕСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ……………………………………..……….. 14 - 8 АВТОКОРРЕЛЯЦИЯ И АВТОСПЕКТР………..………………………… 14 - 9 ВЫЧИСЛЕНИЕ ОТКЛИКА ЛИНЕЙНОЙ СИСТЕМЫ НА ЭРГОДИЧЕСКОЕ СЛУЧАЙНОЕ ВОЗДЕЙСТВИЕ.……………………. 14 - 11 СПЕКТРАЛЬНЫЕ СООТНОШЕНИЯ ДЛЯ ЛИНЕЙНОЙ СИСТЕМЫ С МНОГИМИ ВХОДАМИ И ВЫХОДАМИ..……………… 14 - 12 АНАЛИЗ ОТКЛИКА НА СЛУЧАЙНОЕ ВОЗДЕЙСТВИЕ В MSC.Nastran…………………………………………………..…………. 14 - 16 ОПЕРАТОР RANDPS……………………………………………………… 14 - 17 ОПЕРАТОР TABRND….………………………………………………….. 14 - 19

Анализ отклика на случайное воздействие (продолж.) УПРАВЛЕНИЕ РЕШЕНИЕМ ПРИ АНАЛИЗЕ ОТКЛИКА НА СЛУЧАЙНОЕ ВОЗДЕЙСТВИЕ………………….. 14 - 21 РЕКОМЕНДАЦИИ ПО ВЫПОЛНЕНИЮ РАСЧЕТА..………………...… 14 - 22 ПРИМЕР №10 – ОТКЛИК ПРИ СЛУЧАЙНОМ ВОЗДЕЙСТВИИ ПО ОДНОМУ ВХОДУ………………………………..…. 14 - 23 ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №10...………………………………. 14 - 26 РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №10…………………………….. 14 - 27 ПРИМЕР №11 - ОТКЛИК ПРИ СЛУЧАЙНОМ ВОЗДЕЙСТВИИ ПО НЕСКОЛЬКИМ ВХОДАМ..……………………….. 14 - 35 ВХОДНОЙ ФАЙЛ ДЛЯ ПРИМЕРА №11...……………………………… 14 - 37 РЕЗУЛЬТАТЫ РЕШЕНИЯ ПРИМЕРА №11……………………………. 14 - 40

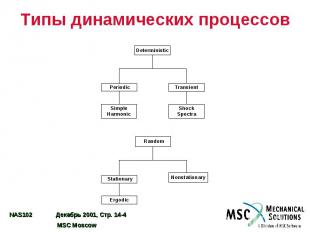
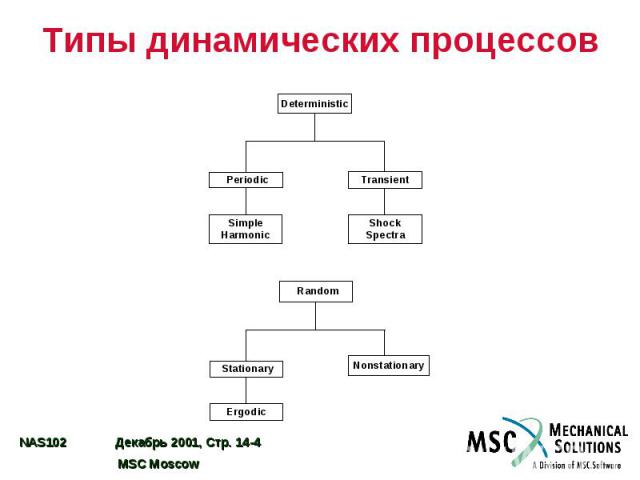
Типы динамических процессов

Анализ отклика на случайное воздействие Случайные колебания – это колебания, которые могут быть описаны только статистически. Их истинное значение в конкретный момент времени неизвестно, чего нельзя сказать о вероятности превышения определенного уровня. Примеры: перемещение почвы при землетрясении, флюктуации давления вокруг самолетов и высоких зданий, акустическое воздействие шума ракетных и авиадвигателей. MSC.Nastran выполняет анализ отклика на случайное воздействие как постпроцессинг анализа частотного отклика. Исходной информацией являются результаты анализа частотного отклика и заданные пользователем нагрузки в форме авто- и взаимных спектральных плотностей. Результаты расчета – спектральные плотности, автокорреляционные функции, значения частоты положительных пересечений нулевого уровня и среднеквадратические отклонения откликов. Теорию см.: Random Vibration in Mechanical Systems, by S. H. Crandall and W. D. Mark, Academic Press, 1963. Дополнительная информация - в MSC.Nastran Advanced Dynamics User’s Guide.

Теория случайных процессов Существуют различные формулировки характеристик случайных процессов. Будьте внимательны при использовании MSC.Nastran (см. MSC.Nastran Advanced Dynamics User’s Guide и книгу Бендата и Пирсола [13] для понимания соответствующих формулировок). При анализе отклика на случайное воздействие с помощью MSC.Nastran предполагается эргодичность процессов. Должна быть ясность в понятиях автокорреляции, автоспектра (спектра мощности), взаимной корреляции и кросспектра. Среднеквадратичное отклонение (значение) и кажущаяся частота – основные статистические характеристики процесса.

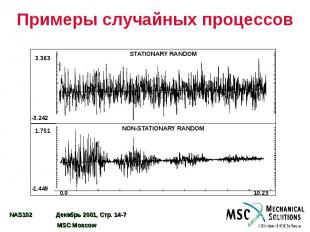
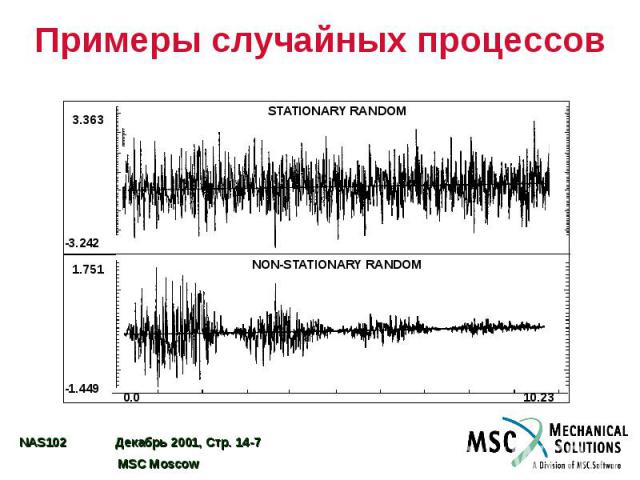
Примеры случайных процессов

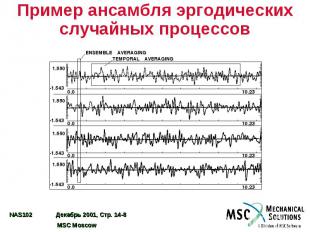
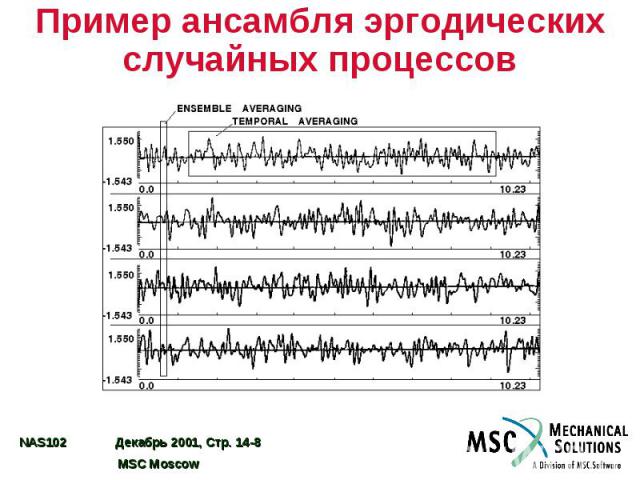
Пример ансамбля эргодических случайных процессов

Автокорреляция и автоспектр Автокорреляционная функция: Примечание: Rj(o) - дисперсия uj(t). Функция автоспектра (спектр, спектральная плотность): Преобразование Фурье: Дисперсия:

Автокорреляция и автоспектр Кажущаяся частота (частота пересечения нулевого уровня) N0:

Вычисление отклика линейной системы на эргодическое случайное воздействие Из анализа частотного отклика где Hja( ) -передаточная функция от входа Fa к выходу uj. При наличии нескольких входов

Спектральные соотношения для линейной системы с многими входами и выходами В матричной форме имеем Fa ( ) uj( ) = [ Hja( ) Hjb( ) … ] Fb ( ) . . Автоспектр на выходе равен Fa ( ) H*ja Sujuj = [ Hja Hjb … ] Fb ( ) [F*a( )F*b( )…] H*jb . . . .

Спектральные соотношения для линейной системы с многими входами и выходами Спектральные характеристики на входе

Спектральные соотношения для линейной системы с многими входами и выходами Входная спектральная матрица Saa( ) Sab( ) … [ S ]in = Sba( ) Sbb( ) … . . . . и ее специальные свойства

Спектральные соотношения для линейной системы с многими входами и выходами Обычно используемые частные случаи Анализ с одним входом (полностью коррелированный вход) Несколько некоррелированных воздействий

Анализ отклика на случайное воздействие в MSC.Nastran Предполагается, что результат анализа частотного отклика - Hja( ). Вычисление не производится. В случае необходимости вычисления Hja( ) задавайте F( ) = 1,0.

Управление решением при анализе отклика на случайное воздействие Executive Control Section SOL (выбирается в соответствие с методом анализа частотного отклика) Case Control Section RANDOM (инициализирует операторы RANDPS, RANDT в Bulk Data Section и должен быть впереди операторов SUBCASE) Bulk Data Section RANDPS (задает значения спектральной плотности мощности) RANDT1 (задает временные сдвиги для вычисления автокорреляционной функции)

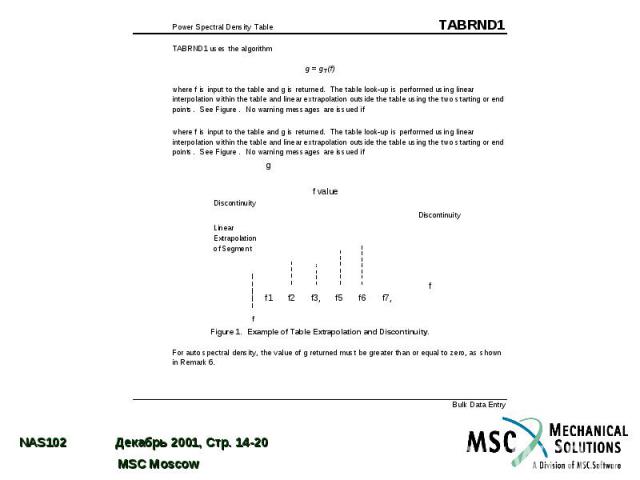
Рекомендации по выполнению расчета В большинстве случаев спектр задают в логарифмических координатах. Используйте соответствующие возможности оператора TABRND1. При возможности всегда вычисляйте входную спектральную плотность (СП). Стройте графики выходной СП. Не пользуйтесь интегральными результатами вслепую. Задавайте несколько частот вблизи каждой моды. При модальном методе для этого хорошо подходят операторы FREQ1 (или FREQ2) и FREQ4. На низких частотах (<20 Гц) задавайте много частот, т.к. спектральная плотность изменяется с частотой быстро при постоянном входном воздействии.

Пример №10 Отклик при случайном воздействии по одному входу

Пример №10. Отклик при случайном воздействии по одному входу Приложите к модели пластины случайное воздействие в направлении Z с заданной СП. Левое ребро соедините с помощью элемента RBE2 с узлом 9999 и приложите вынужденное перемещение к этому узлу Используйте модальное решение с остаточным вектором

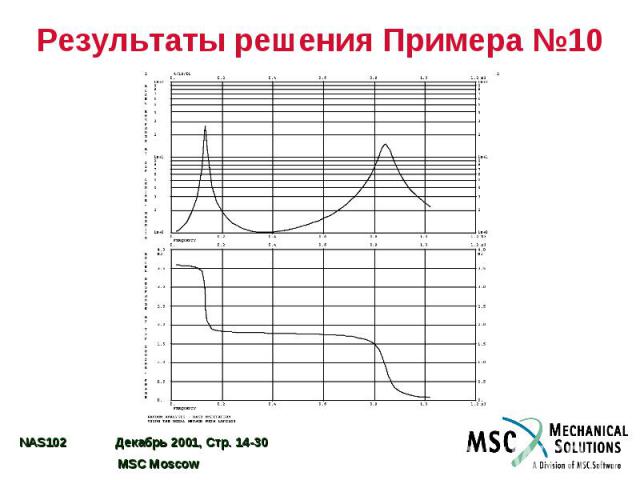
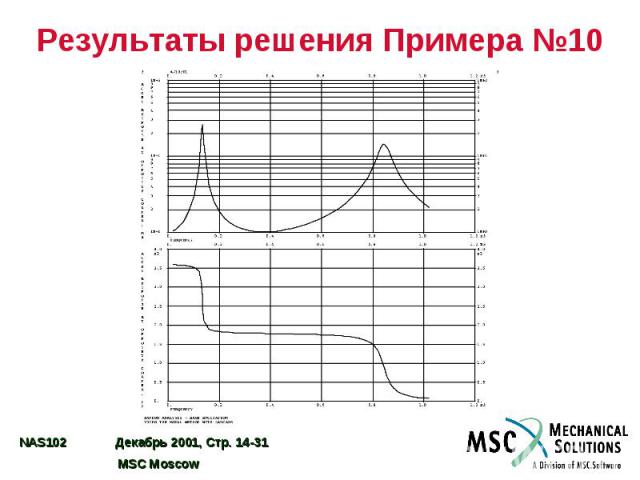
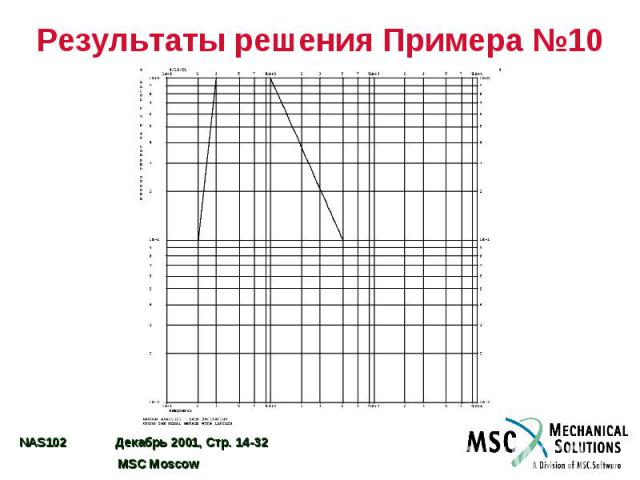
Пример №10. Отклик при случайном воздействии по одному входу Задайте постоянное модальное демпфирование на уровне 0,03 от критического. Используйте задание СП на входе в двойных логарифмических координатах. Определите СП ускорения в точке воздействия, а также в угле и в середине свободного ребра (узлы 33 и 55)

Входной файл для Примера №10 ID SEMINAR, PROB10 SOL 111 CEND TITLE= RANDOM ANALYSIS - BASE EXCITATION SUBTITLE= USING THE MODAL METHOD WITH LANCZOS ECHO= UNSORTED SPC= 101 SET 111= 33, 55, 9999 ACCELERATION(SORT2, PHASE)= 111 METHOD= 100 FREQUENCY= 100 SDAMPING= 100 RANDOM= 100 DLOAD= 100 $ OUTPUT(XYPLOT) XTGRID= YES YTGRID= YES XBGRID= YES YBGRID= YES YTLOG= YES XTITLE= FREQUENCY YTTITLE= ACCEL RESPONSE BASE, MAGNITUDE YBTITLE= ACCEL RESPONSE AT BASE, PHASE XYPLOT ACCEL RESPONSE / 9999 (T3RM, T3IP) YTTITLE= ACCEL RESPONSE AT TIP CENTER, MAGNITUDE YBTITLE= ACCEL RESPONSE AT TIP CENTER, PHASE XYPLOT ACCEL RESPONSE / 33 (T3RM, T3IP) YTTITLE= ACCEL RESPONSE AT OPPOSITE CORNER, MAGNITUDE YBTITLE= ACCEL RESPONSE AT OPPOSETE CORNER, PHASE XYPLOT ACCEL RESPONSE / 55 (T3RM, T3IP) $ $ PLOT OUTPUT IS ONLY MEANS OF VIEWING PSD DATA $ XGRID= YES YGRID= YES XLOG= YES YLOG= YES YTITLE= ACCEL P S D AT LOADED CORNER XYPLOT ACCEL PSDF / 9999(T3) YTITLE= ACCEL P S D AT TIP CENTER XYPLOT ACCEL PSDF / 33(T3) YTITLE= ACCEL P S D AT OPPOSITE CORNER XYPLOT ACCEL PSDF / 55(T3) $

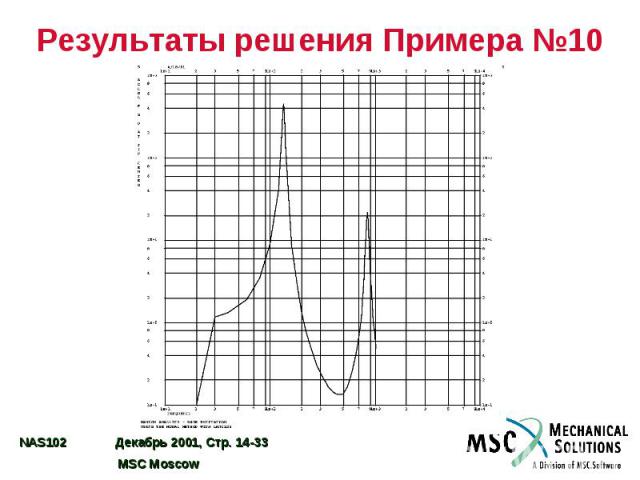
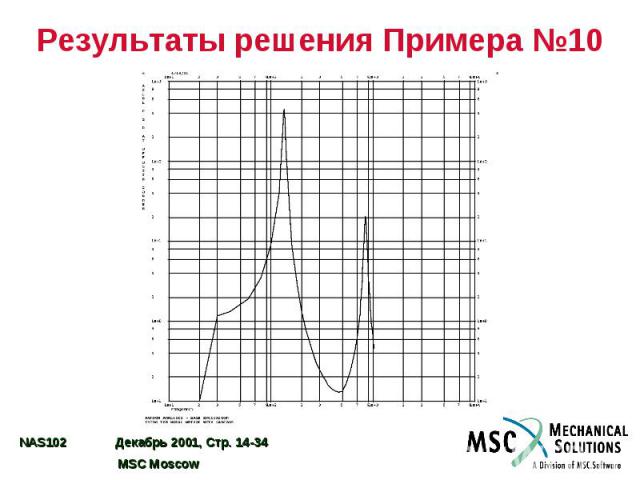
Результаты решения Примера №10

Результаты решения Примера №10

Результаты решения Примера №10

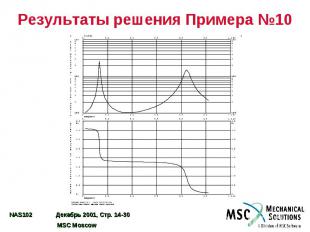
Результаты решения Примера №10

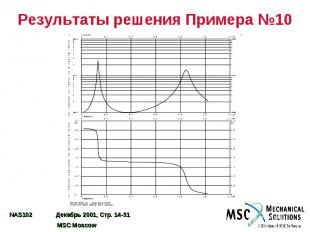
Результаты решения Примера №10

Результаты решения Примера №10

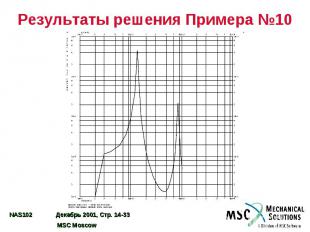
Результаты решения Примера №10

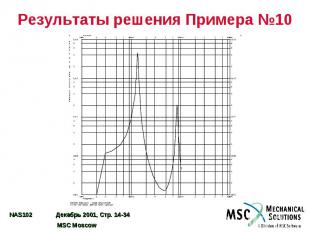
Результаты решения Примера №10

Пример №11 Отклик при случайном воздействии по нескольким входам

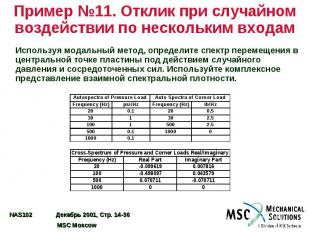
Пример №11. Отклик при случайном воздействии по нескольким входам Используя модальный метод, определите спектр перемещения в центральной точке пластины под действием случайного давления и сосредоточенных сил. Используйте комплексное представление взаимной спектральной плотности.

Входной файл для Примера №11

Входной файл для Примера №11

Входной файл для Примера №11

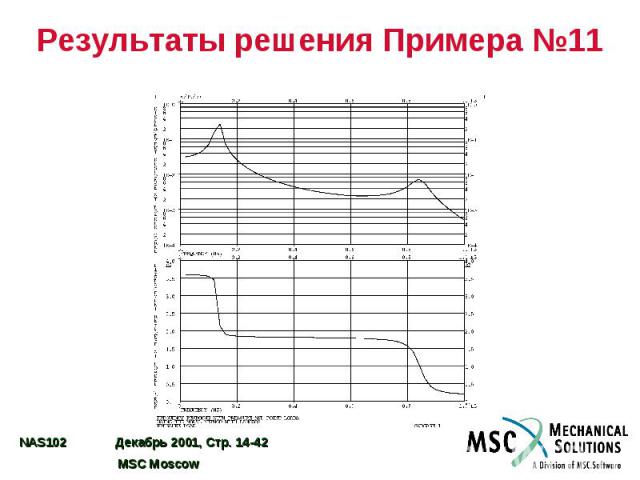
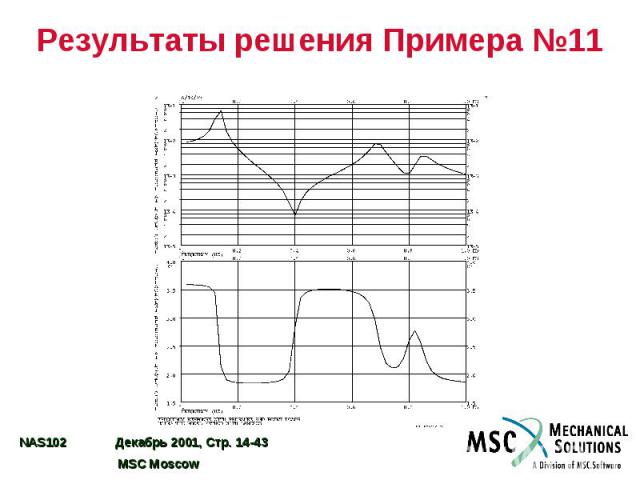
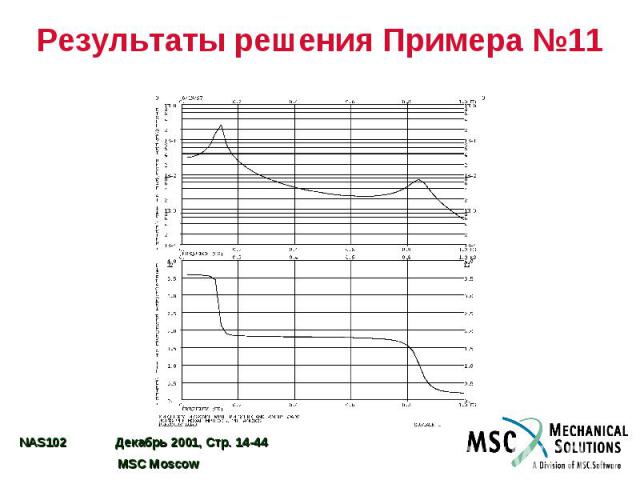
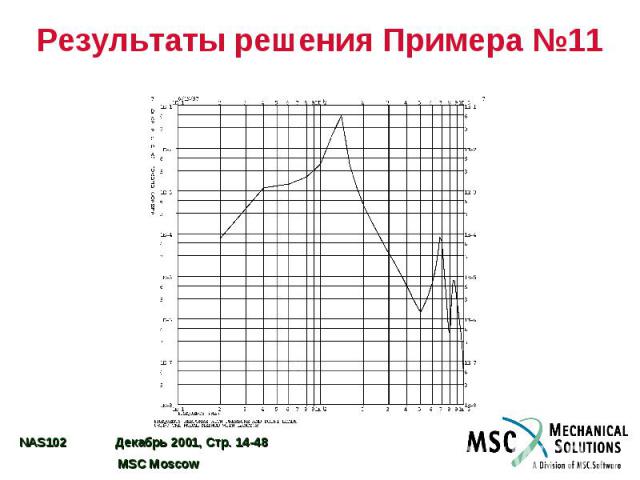
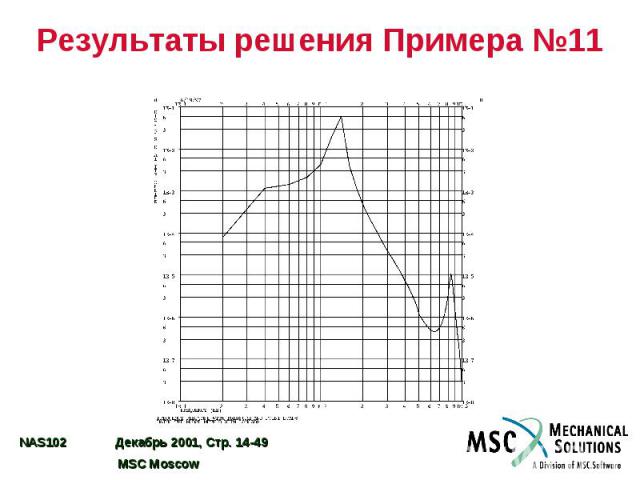
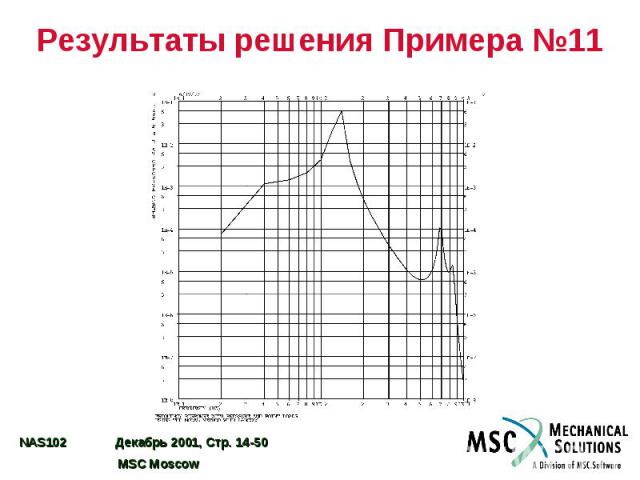
Результаты решения Примера №11

Результаты решения Примера №11

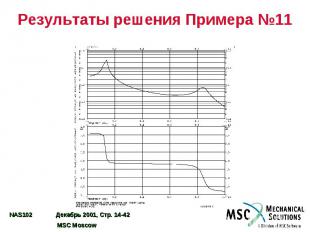
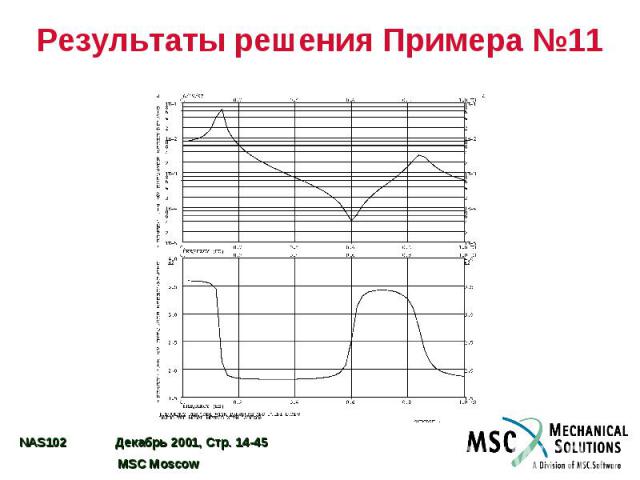
Результаты решения Примера №11

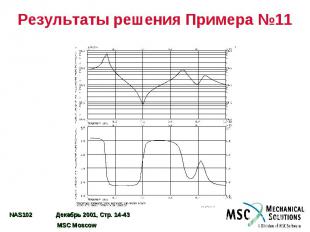
Результаты решения Примера №11

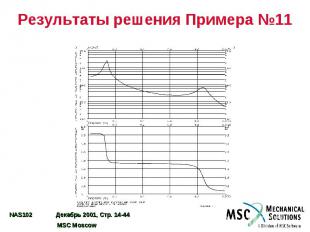
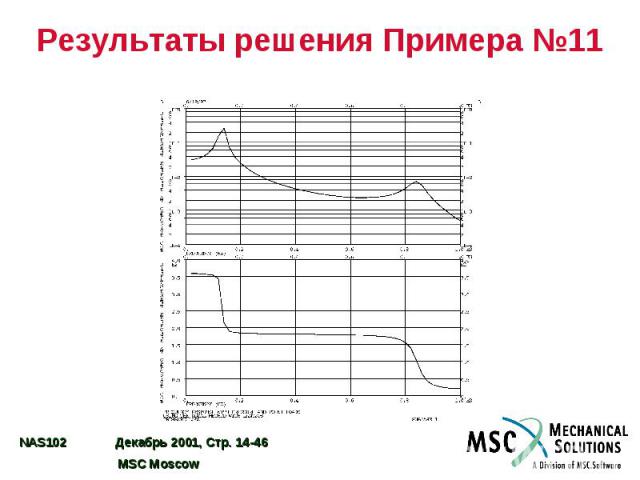
Результаты решения Примера №11

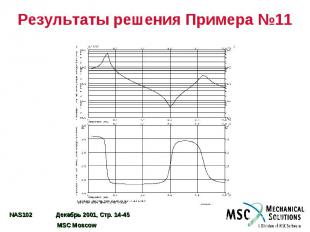
Результаты решения Примера №11

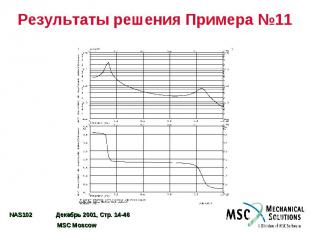
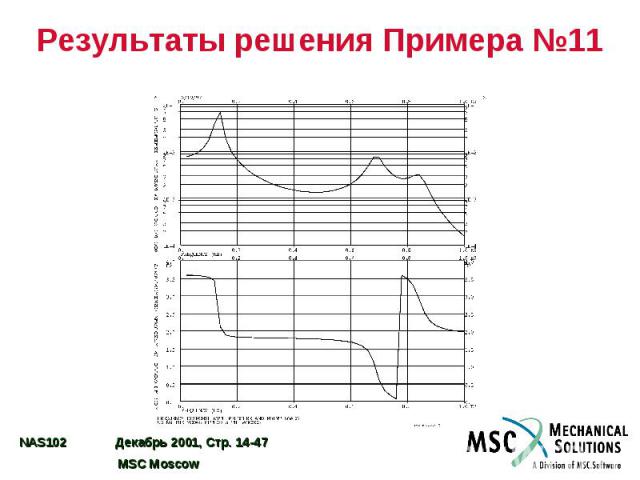
Результаты решения Примера №11

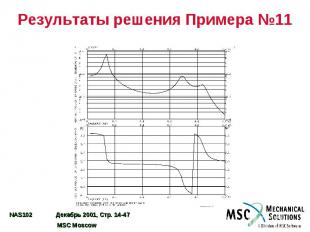
Результаты решения Примера №11

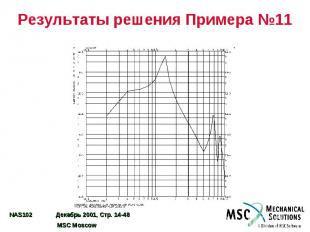
Результаты решения Примера №11

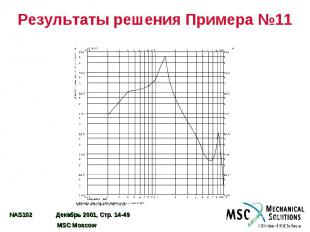
Результаты решения Примера №11

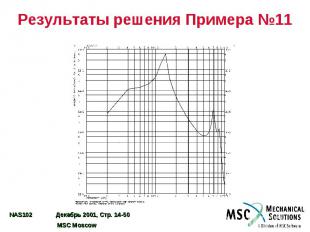
Результаты решения Примера №11