Презентация на тему: MSC.Nastran 101 2006 - 2

Раздел 2 Введение в теорию конечных элементов

Введение в теорию конечных элементов Стр. Основная концепция метода перемещений 6 Интерпретация матрицы жесткости элементов [ke] 8 Моделирование непрерывной конструкции конечными элементами 10 Один элемент: осевое нагружение 13 Общие требования к исходным данным 20 Исходные данные для примера с ROD элементом 23 Глобальная матрица жесткости 44 Процедура анализа сложной конструкции 48 Выходные данные MSC Nastran 52 Проверка модели 53

Введение в теорию конечных элементов (продолжение) Стр. Некоторые советы по моделированию 54 Единицы измерения 56 Обзор процедуры решения методом конечных элементов 58 Литература по матричному анализу 59 Литература по МКЭ 60 Матрица жесткости балочного (BAR) элемента 61 Элемент CBAR 63 Описание CBAR элемента 66 Описание оператора PBAR 74 Расчет момента инерции J для некоторых сечений 76 Поперечный сдвиг 78 Описание CBAR элемента 81

Введение в теорию конечных элементов (продолжение) Стр. Описание оператора PBARL 83 Силы в балочном элементе 89 Пример применения элемента CBAR 91 Входной файл MSC Nastran для данного примера 93 Вывод перемещений для данного примера 94 Вывод сил в элементах для данного примера 95 Вывод напряжений для данного примера 96

Основная концепция метода перемещений Большинство конечноэлементных систем основываются на методе перемещений Каждый элемент модели может быть представлен в виде матрицы жесткости, которая в большинстве случаев называется матрицей жесткости элемента Матрица жесткости элемента зависит от типа элемента и от его характеристик, которые необходимо смоделировать Для одного элемента можно записать уравнение: { P } = [ k ]e { u } (2-1)

Основная концепция метода перемещений (продолжение) где { P } - известные силы, прикладываемые к модели [ k ]e - матрица жесткости [ kij ] , где каждое значение [ kij ] есть сила реакции, действующая по координате i при единичном перемещении по координате j при условии, что все остальные перемещения равны 0; { u } - перемещения полученные решением уравнения (2-1) Для решения уравнения (2-1) и нахождения {u} должны быть приложены соответствующие граничные условия Граничные условия накладываются для устранения перемещений конструкции как твердого тела

Интерпретация матрицы жесткости элемента [k]e [k]e описывает как сила передается через элемент Для упругих задач, закон Максвелла требует, чтобы матрица жесткости была симметричной Математически это означает, что матрица [k]e должна быть квадратной и удовлетворять следующему отношению: kij = kji

Интерпретация матрицы жесткости элемента [k]e (продолжение) Это естественно, поскольку для перемещения конца пружины 1 на заданное расстояние при закрепленном конце 2 требуется приложить такую же нагрузку, что и для перемещения конца 2 на то же расстояние при закрепленном конце 1. Значение одного элемента матрицы жесткости kij называется коэффициентом жесткости. kij имеет размерность нагрузка/перемещение. Размерность kij для пружины – нагрузка/длина (т.е., фунт/дюйм, Н/м)

Моделирование непрерывной конструкции конечными элементами Анализ сложных инженерных задач может быть затруднен (или даже невозможен) без некоторых упрощающих допущений Для конечноэлементного анализа, сложная конструкция подразделяется на некоторое число отдельных (конечных) элементов, которые, в совокупности, аппроксимируют поведение всей конструкции Непрерывная конструкция представляется, как набор точек (узлов), соединяемых элементами

Моделирование непрерывной конструкции конечными элементами (продолжение) Каждая узловая точка имеет шесть независимых степеней свободы (DOFs). Степени свободы определяются как независимые компоненты перемещений или поворотов узловой точки. Непрерывная конструкция теоретически имеет бесконечное количество степеней свободы Идея метода конечных элементов состоит в том, чтобы аппроксимировать поведение конструкции путем сведения бесконечного числа степеней свободы к конечному числу Рисунок 2-1 показывает, что перемещение узловой точки определяется с использованием 6-ти степеней свободы

Моделирование непрерывной конструкции конечными элементами (продолжение) "Перемещение” (displacement) - основной термин означающий компонент перемещения или угла поворота.

Один элемент: осевое нагружение Рассмотрим упругий стержень (ROD) сечением A и длиной L под действием только осевой нагрузки. Заметим, что в MSC Nastran элемент ROD может также воспринимать кручениe, которое в данном примере не рассматривается.

Один элемент: осевое нагружение (продолжение) Для этого ROD элемента, выражение (2-1) может быть представлено как: { P } = [ k ]e { u } (2-2) или P1 AE 1 -1 U1 (2-3) P2 L -1 1 U2 где [k]e = [kij] - известная матрица жесткости ROD элемента, размером 2х2 {P} - вектор известной приложенной силы {u} - вектор неизвестных перемещений, определяемый из уравнения (2-2)

Один элемент: осевое нагружение (продолжение) A - площадь сечения ROD элемента E - модуль Юнга L - длина ROD элемента Неизвестные перемещения, {u}, в уравнении (2-2) (или (2-3)) могут быть найдены следующим образом: { u } = [ k ]e-1 { P } (2-4) На самом деле, для большей эффективности, MSC Nastran использует декомпозицию и прямой-обратный ход (DCMP/FBS) для решения уравнения 2-2 (2-3) вместо обращения матрицы, как это показано в уравнении (2-4).

Один элемент: осевое нагружение (продолжение) Для простоты объяснения в этом семинаре мы будем ссылаться на уравнение (2-4). Мы пока не можем решить данную задачу с ROD элементом, которая показана на рисунке 2-2, так как матрица [k]e-1 сингулярна. Физический смысл сингулярности матрицы состоит в том, что если мы потянем ROD элемент за узел 2, весь элемент начнет перемещаться в осевом направлении, так как ничто не ограничивает его движение (нет закреплений). Математически, два уравнения линейно зависят друг от друга

Один элемент: осевое нагружение (продолжение) Чтобы проиллюстрировать это, распишем уравнение (2-3) следующим образом: P1 = (AE/L)*u1 - (AE/L)*u2 (2-5 a) P2 = – (AE/L)*u1 + (AE/L)*u2 (2-5 b) Заметим, что уравнение (2-5 а) является линейной комбинацией уравнения (2-5 b). Поэтому эти два уравнения линейно зависят друг от друга. Чтобы стабилизировать модель нужно задать соответствующие граничные условия, и тем самым, при действии нагрузки, исключить ее движение как твердого тела.

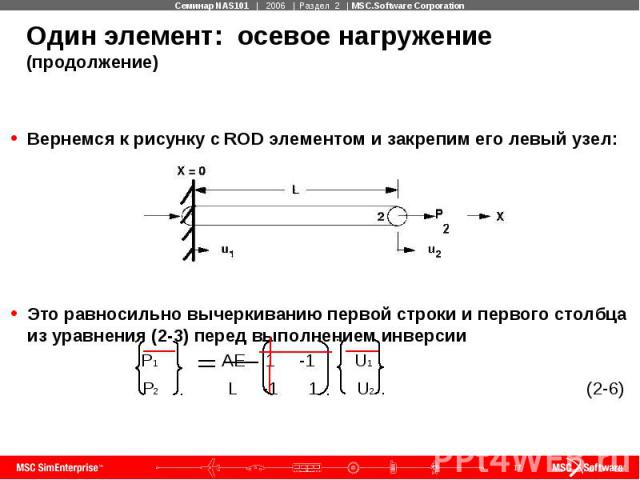
Один элемент: осевое нагружение (продолжение) Вернемся к рисунку с ROD элементом и закрепим его левый узел: Это равносильно вычеркиванию первой строки и первого столбца из уравнения (2-3) перед выполнением инверсии P1 AE 1 -1 U1 P2 L -1 1 U2 (2-6)

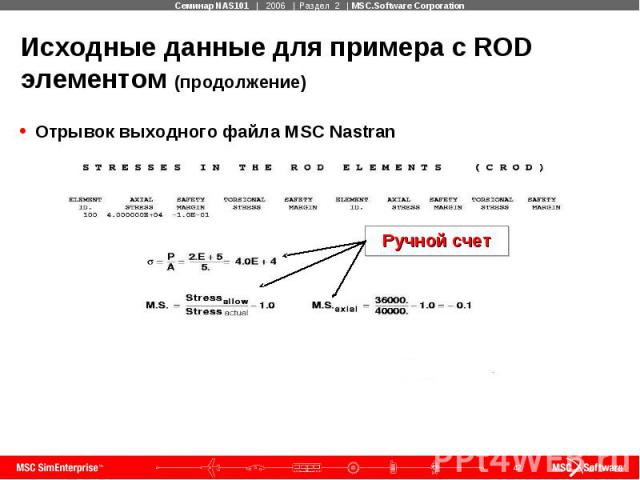
Один элемент: осевое нагружение (продолжение) После закрепления ROD элемента, уравнение (2-6) может быть решено { u } = [ k ]e-1 { P } или u2 = {L/(AE)} * P2 для A = 5.0, L = 100., E = 29. E6, P = 2.E5 u2 = {(100)/(5 * 29E6)} * 2E5 = 0.13791 (перемещение) Fe2 = {(A*E)/L} * u2 = 2.E5 (сила в элементе) = Fe2/A = 2.E5/5. = 4.E4 (напряжение в элементе) Заметим, что Fe2 = P2, так как в данном случае рассматривался только 1 элемент

Общие требования к исходным данным Какие требования существуют для выполнения конечноэлементного анализа? Геометрия Расположение узловых точек (узла 1 и узла 2 в примере с ROD элементом) Направление осей координат, в которых будут получены компоненты сил и перемещений Топология Типы элементов, которые будут использоваться Порядок объединения узловых точек в элементы Свойства элементов Например, толщина для оболочечных элементов или площадь сечения для стержневого элемента. Для каждого типа элемента имеется специфический список свойств.

Общие требования к исходным данным (продолжение) Свойства материала Какой тип материала использовать: алюминий, сталь, графит, эпоксидная смола и т.д.? Свойствами материала являются модуль Юнга, коэффициент Пуассона, плотность, коэффициент температурного расширения и т.д. В MSC Nastran имеются различные типы материалов и каждый имеет специфический список свойств В данном примере использовалось только одно свойство элемента – модуль Юнга Граничные условия (закрепления) Закрепления используются для задания граничных условий, условий симметрии и различных других полезных связей. Закрепления необходимы, так как незакрепленная конструкция может перемещаться в пространстве и ее анализ невозможен. В данном примере ROD элемент был закреплен с левой стороны (за первый узел)

Общие требования к исходным данным (продолжение) Нагрузки Приложенные нагрузки Принудительные перемещения Температурные нагрузки Нагрузки могут прикладываться к узловым точкам или к элементам. В данном примере нагрузка P2 прикладывалась с правой стороны ROD элемента (в узле 2) Что мы хотим получить в результате анализа? Деформации, силы действующие в элементе, напряжения, силы реакции, и т.д.

Исходные данные для примера с ROD элементом Какие общие требования существуют для расчета в системе MSC Nastran? (Те же, что и в общем случае) Геометрия (запись GRID) Топология элементов Свойства элементов Свойства материалов Граничные условия Нагрузки Что нужно получить в результате анализа?

Исходные данные для примера с ROD элементом (продолжение) Геометрия Определяется записью GRID

Исходные данные для примера с ROD элементом (продолжение) Какие общие требования существуют для расчета в системе MSC Nastran? Геометрия (GRID запись) Топология Свойства элементов Свойства материалов Граничные условия Нагрузки Что нужно получить в результате анализа?

Исходные данные для примера с ROD элементом (продолжение) Топология В данном примере топология ROD элемента задается записью CROD

Исходные данные для примера с ROD элементом (продолжение) Какие общие требования существуют для расчета в системе MSC Nastran? Геометрия (GRID запись) Топология Свойства элементов Свойства материалов Граничные условия Нагрузки Что нужно получить в результате анализа?

Исходные данные для примера с ROD элементом (продолжение) Свойства элементов В данном примере свойства ROD элемента определяются с помощью записи PROD

Исходные данные для примера с ROD элементом (продолжение) Какие общие требования существуют для расчета в системе MSC Nastran? Геометрия (GRID запись) Топология Свойства элементов Свойства материалов Граничные условия Нагрузки Что нужно получить в результате анализа?

Исходные данные для примера с ROD элементом (продолжение) Свойства материала Для данной задачи свойства материала описываются записью MAT1 Мы можем задать E, G, и . Из этих величин нужно задать только две, третья автоматически вычисляется из следующего выражения: E – Модуль упругости (Юнга) (при растяжении и изгибе) G – Модуль сдвига (при кручении и сдвиге) - Массовая плотность

Исходные данные для примера с ROD элементом (продолжение) Свойства материала (продолжение) A – Коэффициент линейного температурного расширения Tref – Начальная температура для расчета Т ST,SC,SS – Максимальные (предельные) напряжения при растяжении, сжатии и сдвиге соответственно.

Исходные данные для примера с ROD элементом (продолжение) Свойства материала (продолжение)

Исходные данные для примера с ROD элементом (продолжение) Какие общие требования существуют для расчета в системе MSC Nastran? Геометрия (GRID запись) Топология Свойства элементов Свойства материалов Граничные условия Нагрузки Что нужно получить в результате анализа?

Исходные данные для примера с ROD элементом (продолжение) В MSC Nastran граничные условия могут определяться с использованием записей SPC и SPC1, и/или в поле 8 записи GRID. Для данного примера мы определяем граничные условия в записи GRID (см. страницу 2-23)

Исходные данные для примера с ROD элементом (продолжение) Какие общие требования существуют для расчета в системе MSC Nastran? Геометрия (GRID запись) Топология Свойства элементов Свойства материалов Граничные условия Нагрузки Что нужно получить в результате анализа?

Исходные данные для примера с ROD элементом (продолжение) В данном примере будем использовать запись FORCE

Исходные данные для примера с ROD элементом (продолжение) где

Исходные данные для примера с ROD элементом (продолжение) Для данного примера, Свойства элемента (A = 5.0) Свойства материала (E = 29E+6 psi, G = 11. E+6 psi, y = 36000 psi) Приложенная нагрузка (P = 2.E+5 lbs)

Исходные данные для примера с ROD элементом (продолжение) В результате входной файл выглядит таким образом:

Исходные данные для примера с ROD элементом (продолжение) Какие общие требования существуют для расчета в системе MSC Nastran? Геометрия (GRID запись) Топология Свойства элементов Свойства материалов Граничные условия Нагрузки Что нужно получить в результате анализа?

Исходные данные для примера с ROD элементом (продолжение) В данном примере в результате анализа мы хотим получить перемещения, силы действующие в элементе и напряжения Для этого необходимо сделать запрос в секции Case Control входного файла (позднее данная секция будет рассмотрена более детально) DISP = ALL FORCE = ALL STRESS = ALL

Исходные данные для примера с ROD элементом (продолжение) Отрывок выходного файла MSC Nastran:

Исходные данные для примера с ROD элементом (продолжение) Отрывок выходного файла MSC Nastran

Глобальная матрица жесткости До этого рассматривалась матрица жесткости одного элемента. Теперь рассмотрим глобальную матрицу жесткости реальной конструкции Реальная конструкция может быть представлена как совокупность отдельных элементов Ансамбль матриц жесткости элементов, представляющих конструкцию, называется глобальной матрицей жесткости Для следующих двух ROD элементов с осевым нагружением:

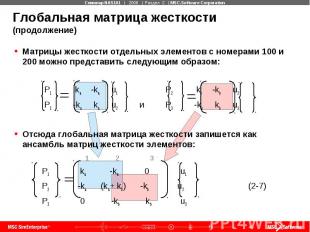
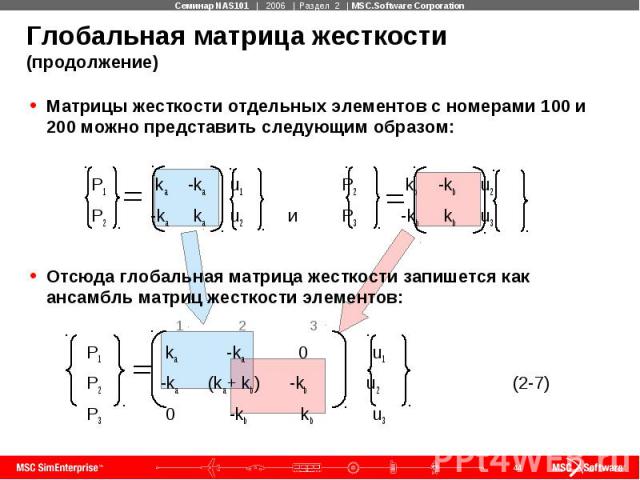
Глобальная матрица жесткости (продолжение) Матрицы жесткости отдельных элементов с номерами 100 и 200 можно представить следующим образом: P1 ka -ka u1 P2 kb -kb u2 P2 -ka ka u2 и P3 -kb kb u3 Отсюда глобальная матрица жесткости запишется как ансамбль матриц жесткости элементов: 1 2 3 P1 ka -ka 0 u1 P2 -ka (ka+ kb) -kb u2 (2-7) P3 0 -kb kb u3

Глобальная матрица жесткости (продолжение) Глобальная матрица жесткости определяется суперпозицией матриц жесткости отдельных элементов Прямое определение матрицы жесткости элемента (т.е. вывод формул вручную) ограничено одно- и двумерными элементами с ограниченным числом степеней свободы Для элементов более высокого порядка (балки, пластины, объемные тела) более целесообразно использовать для формирования матрицы жесткости энергетические принципы и так называемые функции форм элементов

Глобальная матрица жесткости (продолжение) Собрав глобальную матрицу жесткости так, как показано в уравнении (2-7), можно затем решить это уравнение с использованием той же процедуры, что и с одним элементом Эта процедура состоит в следующем: Наложение достаточных граничных условий, путем удаления соответствующих строк и столбцов в уравнении (2-7) При исключении движения конструкции как твердого тела, необходимо помнить, что конечноэлементые системы работают в 3-х мерном пространстве. Это значит, что создаваемый вариант граничных условий должен исключить любое перемещение модели как твердого тела в трех измерениях. Решение { u } = [ K ]-1 { P } Заметим, что для решения MSC Nastran использует процедуру DCMP/FBS вместо обращения матрицы жесткости

Процедура анализа сложной конструкции Процедура, использованная для одного элемента и для двух элементов - может быть расширена для анализа сложной конструкции. Например, при анализе конструкции самолета: Два выделенных стрингера могут быть представлены, например, двумя матрицами жесткости ROD элементов, рассмотренных ранее

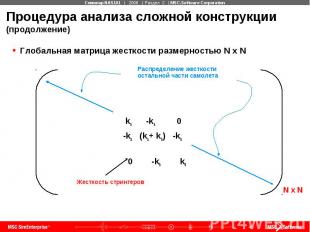
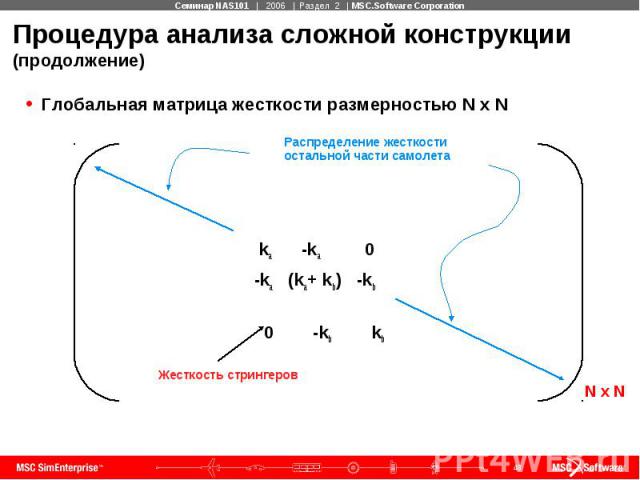
Процедура анализа сложной конструкции (продолжение) Глобальная матрица жесткости размерностью N x N ka -ka 0 -ka (ka+ kb) -kb 0 -kb kb

Процедура анализа сложной конструкции (продолжение) Жесткостные характеристики остальной части самолета находятся составлением ансамбля из отдельных жесткостей элементов, используя тот же самый принцип, рассмотренный для двухэлементной модели Общее поведение конструкции находится с учетом поведения каждого элемента, входящего в нее Пользователь несет ответственность за дискретизацию реальной конструкции на конечные элементы Графический препроцессор MSC Patran поможет Вам сгенерировать конечноэлементную сетку для самой сложной конструкции В общем случае, более качественная и мелкая сетка увеличивает время решения

Процедура анализа сложной конструкции (продолжение) Ресурсы компьютера (время работы центрального процессора), используемые MSC Nastran (при размерности модели в N степеней свободы). Задержки (~ постоянные) Формирование матрицы жесткости (~N); Решение системы уравнений (~N2, постоянно уменьшается с внедрением новых численных методов и применением новых компьютеров); Получение требуемых результатов (~N). Заметим, что конечноэлементная сетка у рассмотренного самолета была очень грубая. Такая сетка была сделана только для более полного понимания процесса составления глобальной матрицы жесткости

Выходные данные MSC Nastran При запуске MSC Nastran Вы можете запросить любую рассчитываемую величину. Вот некоторые из них: Компоненты перемещений узлов Результаты для элементов напряжения деформации энергия деформации внутренние силы и моменты Результаты для узлов прикладываемые нагрузки силы реакций силы, возникающие в узлах

Проверка модели Пользователь должен проверить точность результатов, полученных в результате анализа Некоторые виды проверки выполняются так: Графическое отображение модели для визуальной проверки Проверка ответной реакции модели на приложенную нагрузку Проверка баланса входной нагрузки и сил реакции Проведение ручной проверки результатов, когда это возможно Смотри: Proceedings of the 1986 MSC World Users’ Conference, “MSC Nastran Model Checkout” by the Jet Propulsion Laboratory.

Некоторые советы по моделированию Прежде чем начать моделирование необходимо иметь инженерное представление о поведении конструкции Определите все точки приложения нагрузки и закреплений Разложите общую нагрузку на составляющие: изгибающую, крутящую, сдвиговую и осевую Более тщательно разбейте область, где ожидается большой градиент напряжений. Увеличение числа элементов, как правило, дает возможность повысить точность расчета Попытайтесь использовать симметрию модели Обдумайте затраты компьютерных ресурсов - увеличение числа степеней свободы увеличивает загрузку компьютера, время моделирования и время, необходимое для представления результатов моделирования

Некоторые советы по моделированию (продолжение) Используйте небольшие простые тестовые модели для проверки незнакомых методов и технологий моделирования, прежде чем приступить к дорогостоящему реальному моделированию Вам все равно придется потратить время на создание небольшой модели В конце концов это позволит сэкономить время на отслеживание ошибок и создать более точную модель MSC Nastran ничего не знает о применяемой системе единиц. Физические величины в исходных данных должны задаваться в одной системе единиц Задание всех используемых величин в одной системе измерения остается полностью на совести пользователя Для получения выходных данных в нужной системе единиц входные данные должны быть заданы в ней же

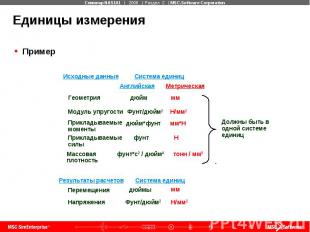
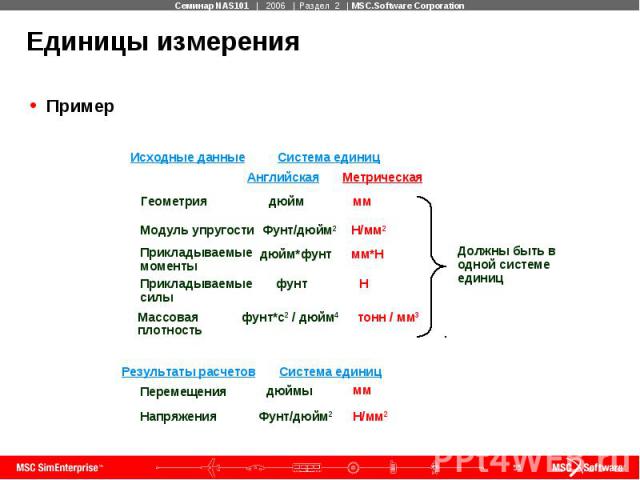
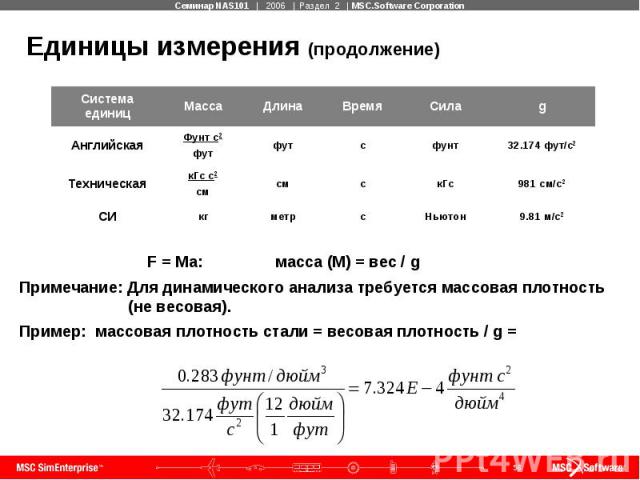
Единицы измерения Пример

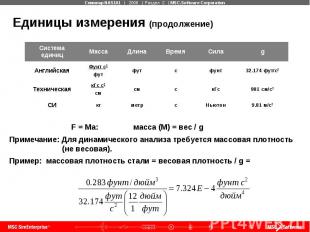
Единицы измерения (продолжение) F = Ma: масса (М) = вес / g Примечание: Для динамического анализа требуется массовая плотность (не весовая). Пример: массовая плотность стали = весовая плотность / g =

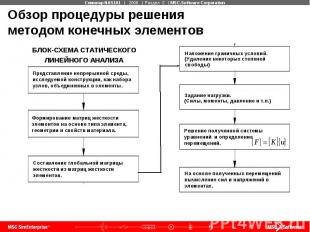
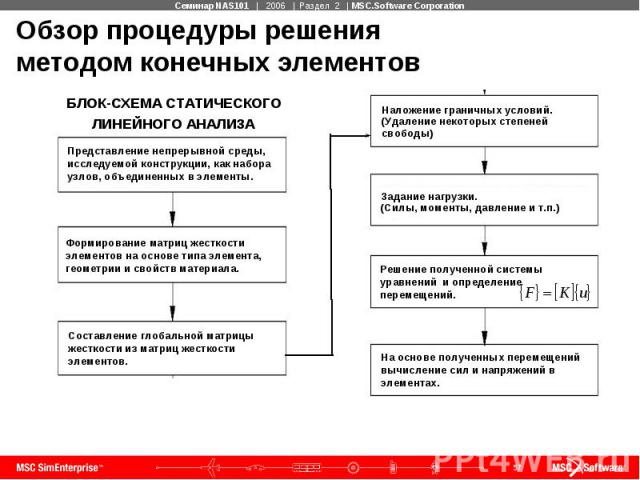
Обзор процедуры решения методом конечных элементов

Литература по матричному анализу

Литература по МКЭ

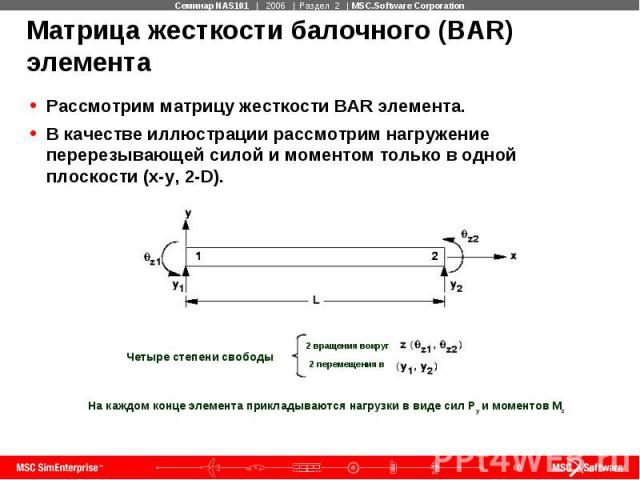
Матрица жесткости балочного (BAR) элемента Рассмотрим матрицу жесткости BAR элемента. В качестве иллюстрации рассмотрим нагружение перерезывающей силой и моментом только в одной плоскости (x-y, 2-D).

Матрица жесткости балочного (BAR) элемента (продолжение) Матрица жесткости для BAR элемента для двухмерной модели, включающей только сдвиг и момент в плоскости x-y: Подобный подход может быть использован для трехмерного BAR элемента, для которого размер матрицы будет 12х12.

Элемент CBAR Соединяет две узловые точки. Формулировки получены из классической балочной теории (плоские сечения остаются плоскими после деформации). По умолчанию используется теория Бернулли-Эйлера (дополнительно можно учесть поперечный сдвиг). Компоненты сил Осевая сила, P Кручение, T Изгибающие моменты в двух перпендикулярных плоскостях, Mi Сдвиг в двух перпендикулярных плоскостях, Vi

Элемент CBAR (продолжение) Компоненты перемещения ui i Нейтральная ось может иметь отступ относительно узловых точек (создается внутренняя жесткая связь) Возможность задания шарниров используется для представления звеньев и т.п. Можно не задавать один из параметров (A, I1, I2, J) Принципиальные ограничения Постоянная призматическая форма (т.е. свойства не зависят от длины)

Элемент CBAR (продолжение) Принципиальные ограничения (продолжение) Центр сдвига и нейтральная ось должны совпадать (поэтому не рекомендуется для моделирования швеллеров) Эффект повышения жесткости при кручении за счет коробления поперечных сечений не учитывается Нет крутильного массового момента инерции Если вышеуказанные ограничения важны, используйте для моделирования BEAM элемент, который этих ограничений не имеет. Смотрите: MSC Nastran Linear Static Analysis User’s Guide или MSC Nastran Reference Manual для более детального описания BAR элемента.

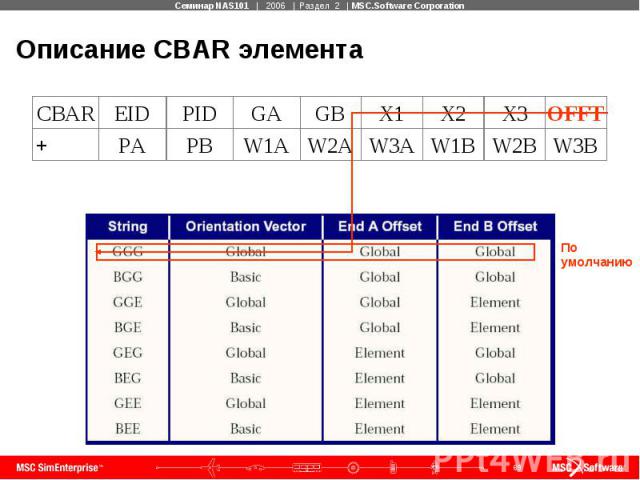
Описание CBAR элемента Топология CBAR элемента

Описание CBAR элемента

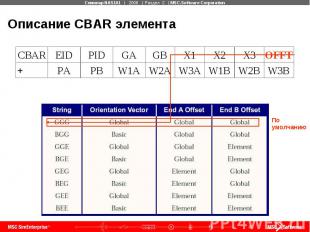
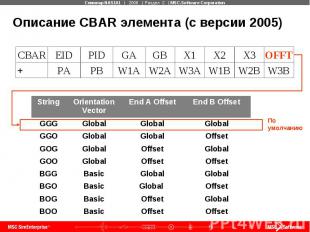
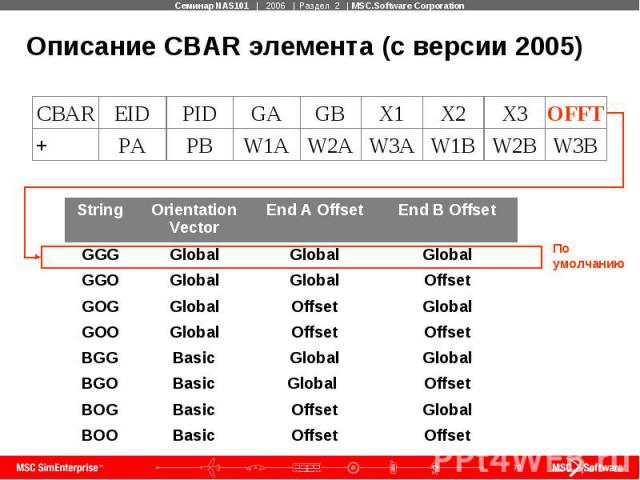
Описание CBAR элемента (с версии 2005)

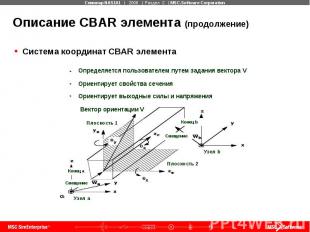
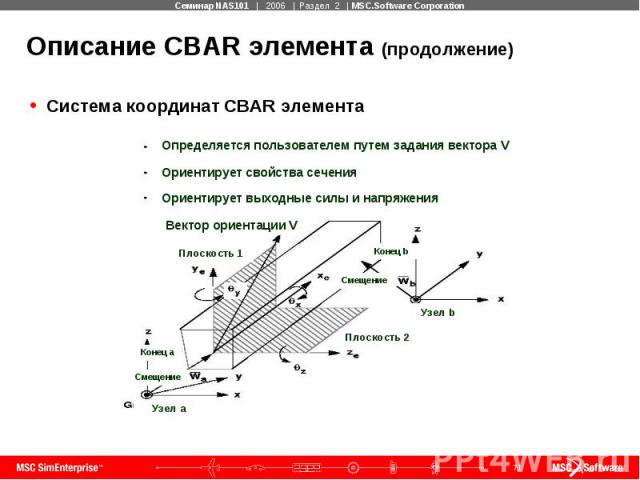
Описание CBAR элемента (продолжение) Система координат CBAR элемента

Описание CBAR элемента (продолжение)

Описание CBAR элемента (продолжение) Далее следуют два примера в которых, задается вектор ориентации системы координат элемента CBAR каждым из двух возможных способов (G0 или X1, X2, X3). Если задавать стрингеры фюзеляжа элементами CBAR, при этом используя способ G0 для определения вектора ориентации, то это значительно облегчит ввод данных

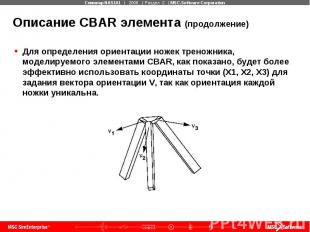
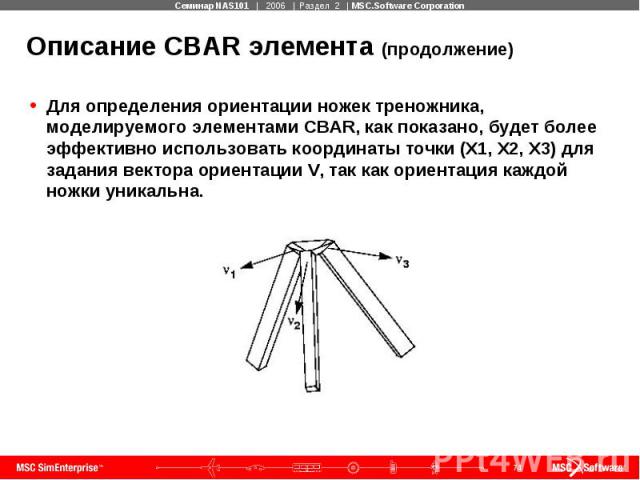
Описание CBAR элемента (продолжение) Для определения ориентации ножек треножника, моделируемого элементами CBAR, как показано, будет более эффективно использовать координаты точки (X1, X2, X3) для задания вектора ориентации V, так как ориентация каждой ножки уникальна.

Описание CBAR элемента (продолжение) Смещения: Концы элемента CBAR могут быть смещены относительно узлов (GA, GB) посредством задания векторов смещения WA и WB в записи CBAR. Вектор смещения можно интерпретировать как жесткую связь между узлами и концами элемента. Система координат элемента определяется с учетом смещения концов BAR элемента.

Описание CBAR элемента (продолжение) Флаги шарниров: Пользователь указывает степени свободы на каждом из концов BAR элемента которые не передают соответствующие силы или моменты. Флаги шарниров PA и PB задаются в системе координат элемента и записываются в полях 2 и 3 в продолжении карты CBAR. Примечание: Флаги шарниров – это силовые ограничения. SPC – это ограничение перемещений.

Описание оператора PBAR Свойства CBAR элемента записываются операторами PBAR или PBARL:

Описание оператора PBAR (продолжение)

Расчет моментов инерции J для некоторых сечений

Расчет моментов инерции J для некоторых сечений (продолжение)

Поперечный сдвиг Сдвиговые перемещения балки - V, рассчитываются по формуле V = ( Fz * L ) / ( K * A * G) где: Fz - силы сдвига в направлении Z элемента L - длина балки K - коэффициент сдвига A - площадь сечения G - модуль сдвига балки и величина 1/K*A*G называется сдвиговой податливостью балки

Поперечный сдвиг (продолжение) K определяет распределение сдвига по сечению элемента и ее величина зависит от формы сечения. В записи PBAR: K1 сопротивление сдвигу в направлении оси Y элемента. K2 сопротивление сдвигу в направлении оси Z элемента.

Поперечный сдвиг (продолжение) Значения К для некоторых сечений Литература: Roark and Young, Formulas for Stress and Strain, 5th ed., стр. 185.

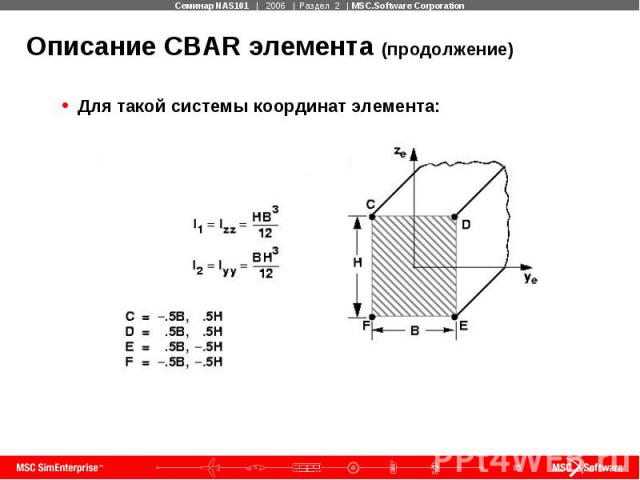
Описание CBAR элемента (продолжение) Ориентация системы координат элемента определяет плоскости сечения 1 и 2, ориентацию моментов инерции, выводимые при расчете напряжения. Для этой системы координат элемента:

Описание CBAR элемента (продолжение) Для такой системы координат элемента:

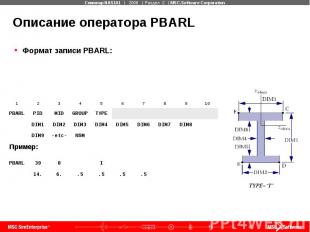
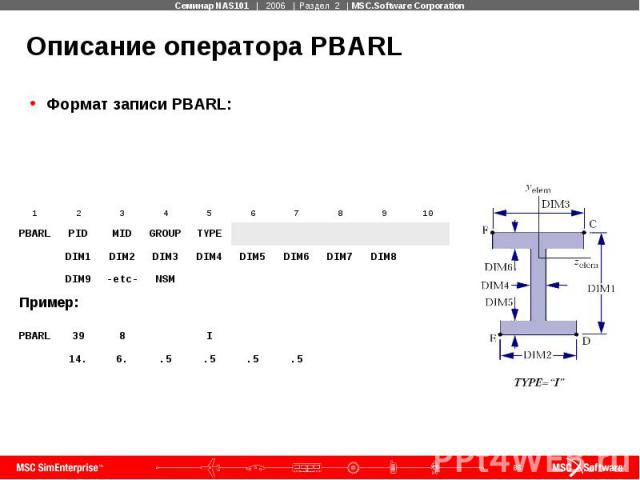
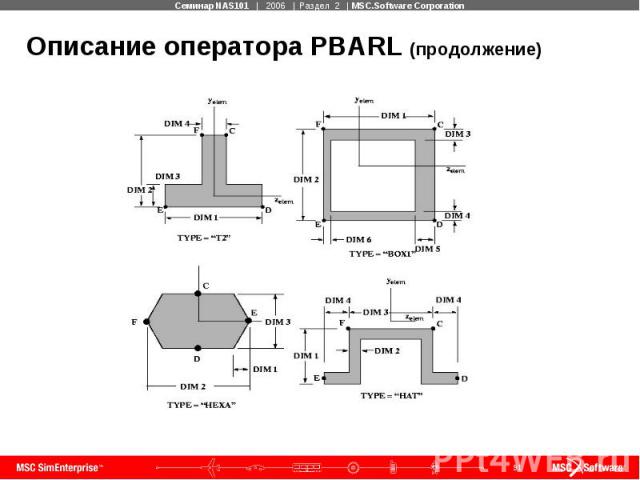
Описание оператора PBARL Формат записи PBARL:

Описание оператора PBARL (продолжение) где:

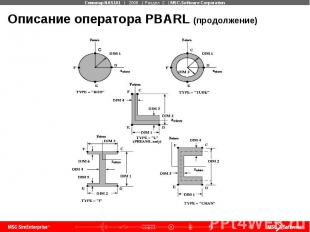
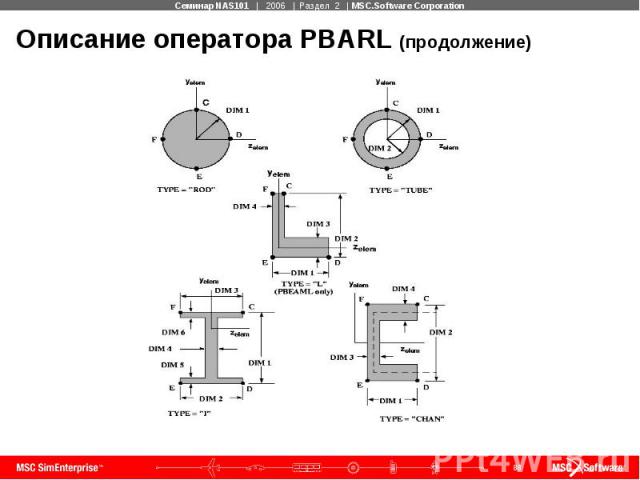
Описание оператора PBARL (продолжение)

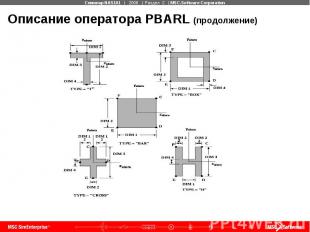
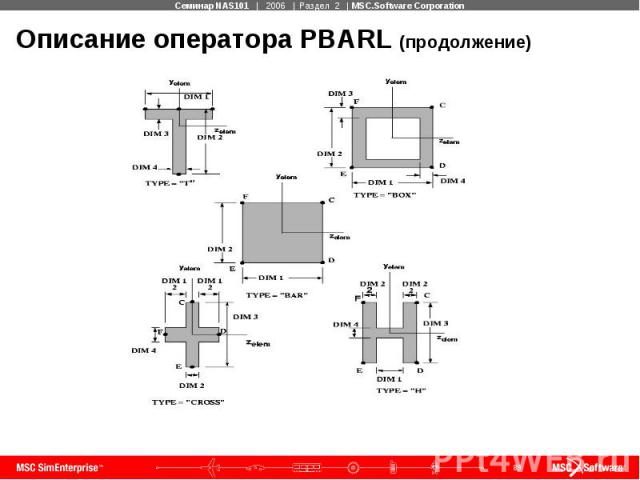
Описание оператора PBARL (продолжение)

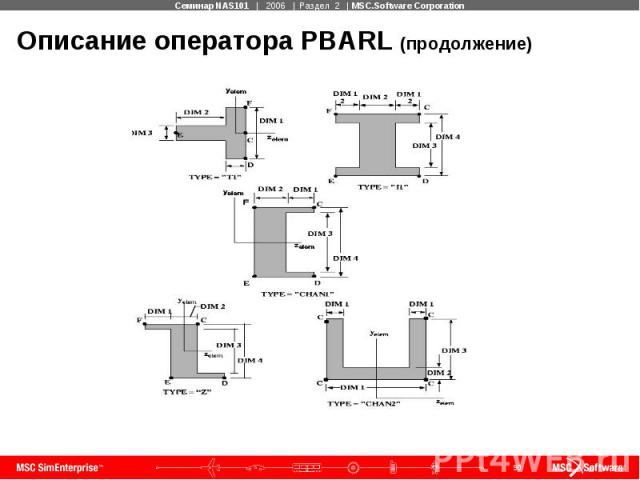
Описание оператора PBARL (продолжение)

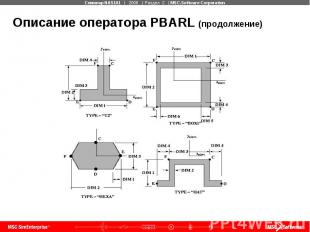
Описание оператора PBARL (продолжение)

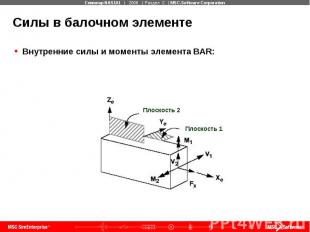
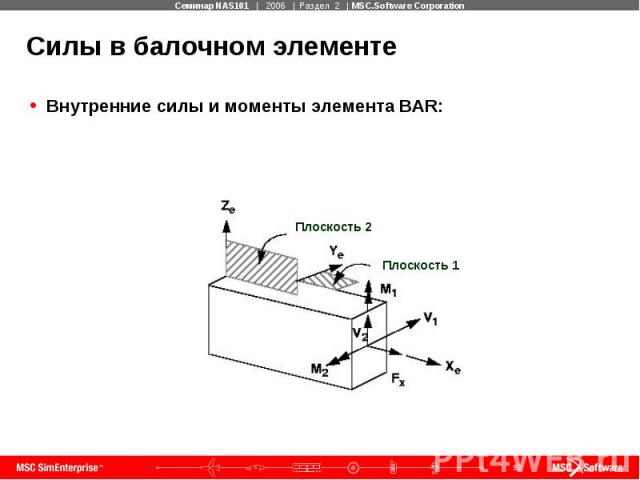
Силы в балочном элементе Внутренние силы и моменты элемента BAR:

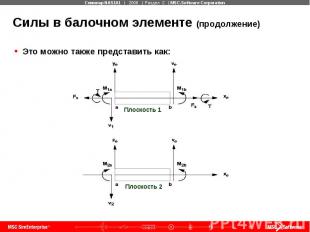
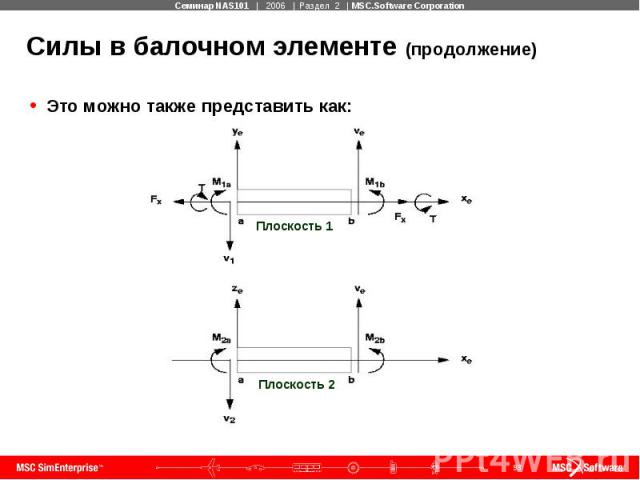
Силы в балочном элементе (продолжение) Это можно также представить как:

Пример применения CBAR элемента

Пример применения CBAR элемента (продолжение) Свойства

Входной файл MSC Nastran для данного примера

Вывод перемещений для данного примера

Вывод сил в элементе для данного примера

Вывод напряжений для данного примера