Презентация на тему: MSC.Flightloads 5.1а

Раздел 5.1a Расчет линейной статической аэроупругости


Описание задачи Основное уравнение линейной аэроупругости записывается в виде Известны внешние нагрузки и известна часть балансировочных параметров . Задача: определить остальные балансировочные параметры и упругие деформации . Затем могут быть определены нагрузки, действующие на ЛА.

Последовательность Сначала производится расчет балансировки жесткого ЛА. Затем, с учетом эффекта упругости. Для упругих деформаций используются 2 системы отсчета: В Restrained Analysis (расчет с защемление) используется СК, связанная с r-множеством степеней свободы. В Unrestrained Analysis (расчет без защемления) используется основная (связанная) СК.

«Жесткий» ЛА Если принебречь упругостью ЛА, то для балансировки требуется только результирующие силы. Уравнение равновесия результирующих сил получают проецированием основного уравнения на твердотельные формы При проецирование даст где матрица масс твердого тела.
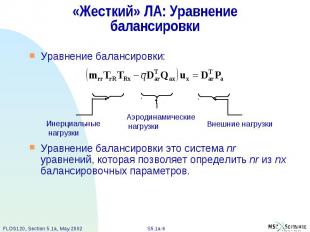
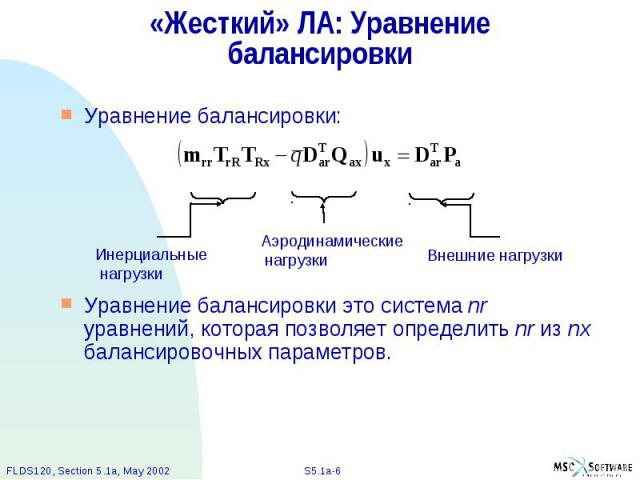
«Жесткий» ЛА: Уравнение балансировки Уравнение балансировки: Уравнение балансировки это система nr уравнений, которая позволяет определить nr из nx балансировочных параметров.

«Жесткий» ЛА: Пример 1 Маневр: стационарный продольный полет

«Жесткий» ЛА: Пример 2 Маневр: внезапное отклонение элерона

Виды задач В первом примере все балансировочные параметры постоянны во времени. Такая задача может называться стационарным балансировочным расчетом. Во втором примере балансировочные параметры зависят от времени. Уравнение балансировки решается только для одного фиксированного момента времени. Такая задача может называться мгновенным балансировочным расчетом. Мгновенный балансировочный расчет является квазистатической аппроксимацией динамической задачи.

Чрезмерная балансировка Число свободных балансировочных параметров может превышать число степеней свободы r- множества. В этом случае свободные балансировочные параметры определяются из условий что уравнение балансировки выполняется и Сумма квадратов балансировочных параметров минимальна
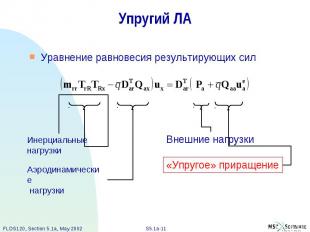
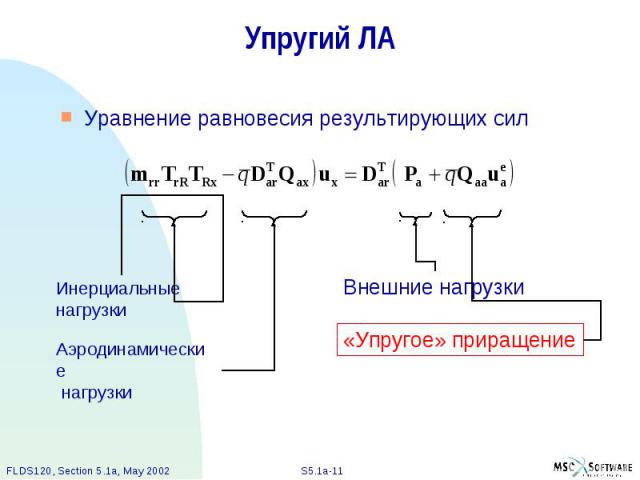
Упругий ЛА Уравнение равновесия результирующих сил

Упругие деформации Упругие деформации должны быть линейно независимыми от форм твердого тела Таким образом они могут быть записаны в виде nl = na – nr число столбцов матрицы - основная матрица упругих деформаций. Только при выполнении этого условия деформации будут линейно независимыми от форм твердого тела .

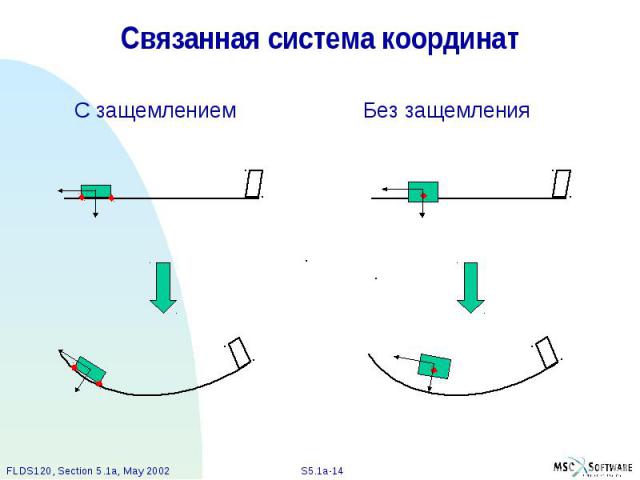
Связанная система координат Упругие деформации отображаются относительно связанной СК В restrained analysis (расчет с защемлением), связанная СК движется вместе с твердым телом, присоединенная к r-множеству степеней свободы. Упругие перемещения r-множества степеней свободы равны 0. В unrestrained analysis (расчет без защемления), связанная СК движется с твердым телом, присоединенная к центру масс и главным осям инерции. Эта система называется системой средних осей.
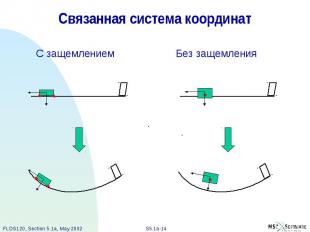
Связанная система координат

Restrained Analysis: упругий базис Упругим базисом удобно называть где nl-разммерная единичная матрица и - вырожденная матрица с nr строками и nl столбцами. Значить следовательно

Restrained Analysis: уравнение упругости Система nl уравнений получается проецированием основного уравнения на упругий базис: Индексом l обозначена часть матриц I-множества, соответствующая матрицам a-множества. Эта система уравнений позволяет записать уравнение упругих деформаций как функцию от балансировочных параметров и приложенных нагрузок.

Restrained Analysis: Основное решение За счет деформаций вносятся аэроупругие поправки во внешние нагрузки: Деформации, за счет которых вносятся аэроупругие поправки в нагрузки, вызванные единичными балансировочными параметрами (единичное решение): В таком случае
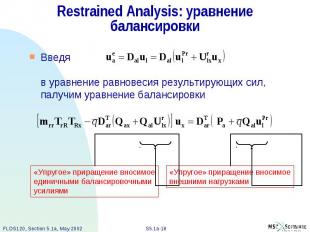
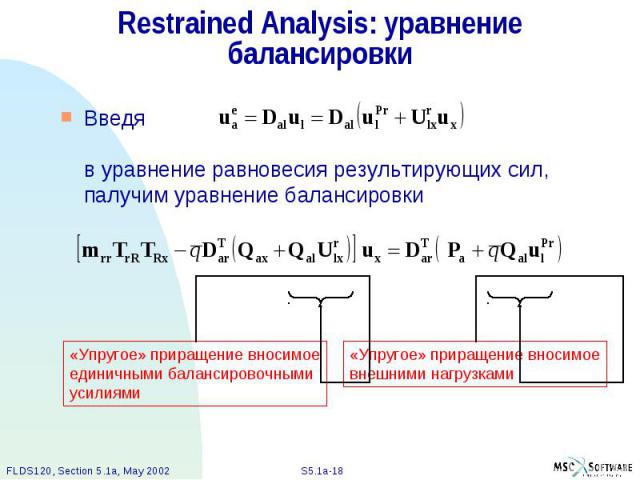
Restrained Analysis: уравнение балансировки Введя в уравнение равновесия результирующих сил, палучим уравнение балансировки

Unrestrained Analysis: Упругий базис Условие «средних осей» Упругим базисом удобно называть Следствием условия «средних осей» является то, что твердотельные ускорения не вызывают упругие деформации.

Unrestrained Analysis: уравнение упругости Проецируя основное уравнение на упругий базис получаем уравнение упругости где Инерциальные члены исчезли, так как использовалось условие «средних осей».

Unrestrained Analysis: Основное решение За счет деформаций вносятся аэроупругие поправки во внешние нагрузки: Деформации, за счет которых вносятся аэроупругие поправки в нагрузки, вызванные единичными балансировочными параметрами (единичное решение): В таком случае

Unrestrained Analysis: Уравнение балансировки Подставляя основное решениие в уравнение равновесия результирующих сил, получим уравнение балансировки Заметьте, что «упругие» приращения не зависимы на твердотельных ускорениях поэтому единичное решение отсутствует.

Производные устойчивости: Определение Производные устойчивости – производные от коэффициентов аэродинамических нагрузок относительно балансировочных параметров. Производные устойчивости относятся к связанной системе координат. Результирующая аэродинамических нагрузок запишется в виде

Производные устойчивости : Нормирование Коэффициент результирующей эродинамической нагрузки где

Производные устойчивости : Расчет В общем виде: «Жесткий» ЛА: Restrained Analysis: Unrestrained Analysis: