Презентация на тему: MSC.Dytran - 15

СОДЕРЖАНИЕ Определение (задание) элемента Топология эйлеровых элементов Типы эйлеровых элементов Материалы Начальные условия Эйлеровы граничные условия Автоматический генератор эйлеровой сетки ROE-решатель Вывод результатов

ОПРЕДЕЛЕНИЕ (ЗАДАНИЕ) ЭЛЕМЕНТА Для определения элемента необходимо задать: Координаты узлов Координаты узлов задаются операторами GRID Топологию элементов Топология элементов задаётся операторами CHEXA / CPENTA / CTETRA Свойства элемента Свойства элемента (математическая формулировка) задаются операторами PEULER или PEULER1 Материал Оператор DMAT используется для задания параметров материала Каждый оператор должен иметь свой уникальный идентификатор (ID)

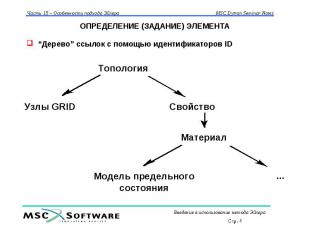
ОПРЕДЕЛЕНИЕ (ЗАДАНИЕ) ЭЛЕМЕНТА “Дерево” ссылок с помощью идентификаторов ID

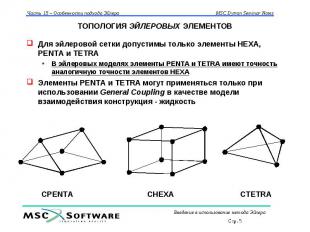
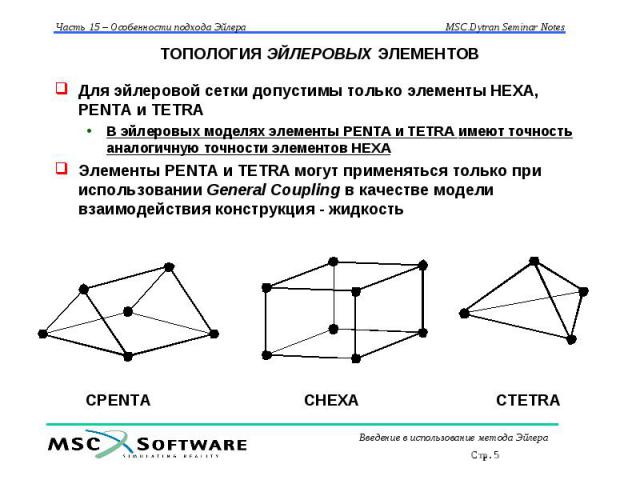
ТОПОЛОГИЯ ЭЙЛЕРОВЫХ ЭЛЕМЕНТОВ Для эйлеровой сетки допустимы только элементы HEXA, PENTA и TETRA В эйлеровых моделях элементы PENTA и TETRA имеют точность аналогичную точности элементов HEXA Элементы PENTA и TETRA могут применяться только при использовании General Coupling в качестве модели взаимодействия конструкция - жидкость

ТИПЫ ЭЙЛЕРОВЫХ ЭЛЕМЕНТОВ Имеются четыре типа эйлеровых элементов Полное или частичное заполнение только одним материалом с гидродинамическим “поведением” Тензор напряжений в материале представлен только гидравлическим давлением; вычислительные затраты невелики PEULER, 100, 2, HYDRO Полное или частичное заполнение только одним материалом со сдвиговыми напряжениями Тензор напряжений представлен сдвиговыми напряжениями и гидравлическим давлением; сравнительно большие вычислительные затраты PEULER, 100, 2, STRENGTH Полное или частичное заполнение различными материалами с гидродинамическим “поведением” Тензор напряжений материалов в элементе представлен только гидравлическим давлением Нет ограничений на количество материалов в расчётной схеме, однако в одном отдельно взятом элементе может быть не более 5 материалов PEULER, 100, 2, MMHYDRO Полное или частичное заполнение различными материалами со сдвиговыми напряжениями Тензор напряжений представлен сдвиговыми напряжениями и гидравлическим давлением, однако, опять же, в каждом элементе не может быть более 5 материалов PEULER, 100, 2, MMSTREN

ПРИМЕНЯЕМОСТЬ ЭЛЕМЕНТОВ Эйлеров материал с гидродинамическим “поведением” применяется для моделирования Жидкостей Газов Эйлеров материал со сдвиговыми напряжениями применяются для моделирования Объёмных тел с большими деформациями Вязких жидкостей Вязких газов

МАТЕРИАЛЫ Оператор DMAT применяется для описания всех типов материалов для эйлеровых моделей с различными уравнениями состояния, моделями сдвиговых свойств, предельного состояния, разрушения, разрыва и т.п. DMAT, mid, rho, eid, sid, yid, fid, pid

НАЧАЛЬНЫЕ УСЛОВИЯ Оператор TICEL – задание начальных условий (параметров среды) для элементов Оператор TICEL ссылается на оператор SET1, определяющий список элементов, для которых задаются начальные условия Пример: задание начального значения плотности и скорости движения среды в направлении x PEULER, 666, 2, HYDRO DMAT, 2, 1.114, 4 EOSGAM, 4, 1.4, 293. … TICEL, 3, 100, DENSITY, 1.114, XVEL, 100. SET1, 100, <список элементов>

НАЧАЛЬНЫЕ УСЛОВИЯ Инициализация плотности по умолчанию Если начальное значение плотности не задано в операторе TICEL, то она принимает значение, указанное в операторе DMAT Инициализация давления Давление инициализируется в соответствии с уравнением состояния Пример для случая уравнения состояния идеального газа: Pinitial = ( - 1) · initial · einitial Если задать давление с помощью оператора TICEL, то оно будет переопределено на значение, вычисленное по указанному выше выражению

НАЧАЛЬНЫЕ УСЛОВИЯ Оператор TICEUL – задание начальных условий (параметров среды) для геометрического региона (зоны) Свойства эйлеровых элементов задаются оператором PEULER1 Оператор PEULER1 ссылается на оператор TICEUL Пример: PEULER1, 777, , HYDRO, 333 … TICEUL, 333, … Оператор TICEUL определяет регионы, которым при инициализации будут назначены Материал Начальные значения переменных Форма геометрических регионов Сфера Цилиндр Поверхность Блок (набор) элементов Каждому геометрическому региону присваивается свой индекс Регионы могут перекрываться в пространстве и регион с большим значением индекса будет иметь больший приоритет

НАЧАЛЬНЫЕ УСЛОВИЯ Пример 1: цифры на рисунке показывают принадлежность элементов в разных зонах модели к трём заданным регионам

НАЧАЛЬНЫЕ УСЛОВИЯ Пример 2: 1000 объёмных элементов со свойством PID=111 будут инициализированы как эйлеровы элементы с возможностью заполнения несколькими материалами Эти 1000 элементы инициализируются как заполненные материалом 444 с начальными параметрами, указанными в операторе TICVAL 555 Однако, элементы, находящиеся внутри сферы с центром в точке с координатами (0,0,0) и радиусом 0,1, инициализируются как заполненные материалом 222 с начальными параметрами, указанными в операторе TICVAL 333 PEULER1, 111, , MMHYDRO, 777 DMAT, 222, 1000., 5 DMAT, 444, 1.114, 6 TICEUL, 777, , , , , , , , + +, SPHERE, 888, 222, 333, 10., , , , + +, ELEM, 999, 444, 555, 1. SPHERE, 888, , 0., 0., 0., 0.1 TICVAL, 333, , XVEL, 100. SET1, 999, 1, THRU, 1000 TICVAL, 555, , XVEL, 500.

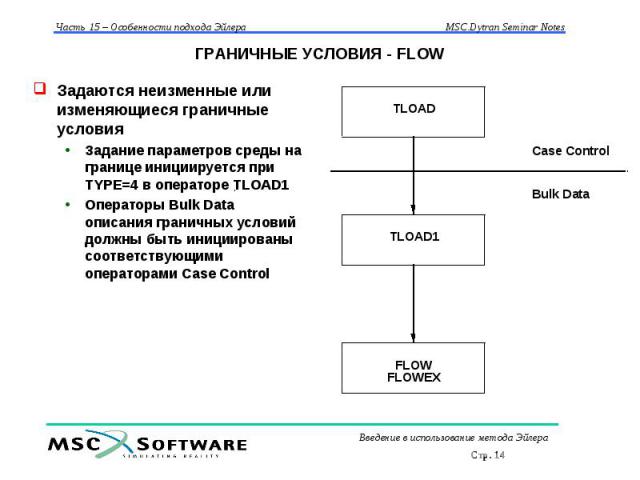
ГРАНИЧНЫЕ УСЛОВИЯ - FLOW Задаются неизменные или изменяющиеся граничные условия Задание параметров среды на границе инициируется при TYPE=4 в операторе TLOAD1 Операторы Bulk Data описания граничных условий должны быть инициированы соответствующими операторами Case Control

ГРАНИЧНЫЕ УСЛОВИЯ - FLOW Операторы TLOAD1 и FLOW определяют эйлеровы граничные условия – параметры среды на границе Под границей понимается набор сегментов, перечисленных в операторах CFACEn Пример: CFACE1, 222, 200, 6 TLOAD1, 1, 333, 4 FLOW, 333, 222, XVEL, 100, PRESSURE, 1.0E5 Операторы TLOAD1 и FLOWEX используются для задания граничных условий посредством пользовательской подпрограммы Граница определяется как набор сегментов, перечисленных в операторах CFACEn) Пользователь должен позаботиться о собственной подпрограмме EXFLOW Пример: CFACE1, 222, 200, 6 TLOAD1, 1, 333, 4 FLOWEX, 333, 222, USERFLOW

ГРАНИЧНЫЕ УСЛОВИЯ - WALLET Оператор WALLET описывает барьер внутри эйлеровой сетки, препятствующий движению (течению) материала Барьер задаётся в виде набора сегментов, перечисленных в операторах CFACEn Пример: CFACE1, 222, 200, 6 WALLET, 100, 222

ГРАНИЧНЫЕ УСЛОВИЯ - DEFAULT По умолчанию на границах эйлеровой сетки автоматически генерируются граничные условия “барьер” (задаваемые оператором WALLET) С помощью оператора FLOWDEF граничные условия по умолчанию на границах эйлеровой сетки могут быть переопределены Пример: на границах эйлеровой сетки задаётся постоянное давление 1·105 FLOWDEF, 44, , HYDRO, , , , , , + +, PRESSURE, 1.0E5

АВТОМАТИЧЕСКАЯ ГЕНЕРАЦИЯ ЭЙЛЕРОВОЙ СЕТКИ Оператор MESH (TYPE=BOX) – автоматическая генерация ортогональной эйлеровой сетки Пример: генерация эйлеровой сетки с “начальной точкой” (0,0,0), размерами пространства 5 5 5, количеством элементов в каждом направлении 20, номером первого узла 1001, номером первого элемента 2001, типом свойства (EULER) и номером оператора описания свойства элементов 1 MESH, 1, BOX, , , , , , , + +, 0., 0., 0., 5., 5., 5., , , + +, 20, 20, 20, , 1001, 2001, EULER, 1 Оператор MESH (TYPE=ADAPT) – автоматическая генерация ортогональной эйлеровой сетки в областях пространства, в которых поверхность взаимодействия с конструкцией перемещается “наружу” (начиная с версии MSC.Dytran 2002r2) Пример: автоматическая генерация эйлеровой сетки с размером элемента во всех направлениях 0,25, с номером первого вновь созданного узла 1001 и номером первого вновь созданного элемента (со свойством 11) 2001 MESH, 1, ADAPT, 0.25, 0.25, 0.25, 0., 0., 0., + +, , , , , , , 1, OUTSIDE, + +, , , , , 1001, 2001, EULER, 11

ROE-РЕШАТЕЛЬ Эйлеров решатель, основанный на алгоритме Riemann’а, разработанного проф. Ф. Рое (Phillip Roe) 1-ый или 2-ой порядок пространственной аппроксимации 2-ой порядок (принят по умолчанию) обеспечивает отсутствие осцилляций решения в области существенных изменений параметров течения среды Примеры: PARAM,LIMITER,ROE,NONE – первый порядок аппроксимации PARAM,LIMITER,ROE – второй порядок аппроксимации Для интегрирования во временной области используется многошаговый алгоритм Рунге-Кутты PARAM,RKSCHEME,1 PARAM,RKSCHEME,3 При применении ROE-решателя использование модели материала (уравнение состояния) JWL недопустимо – необходимо использовать “обычную” технологию При применении ROE-решателя допустимо наличие в модели только одного материала, “пустые” зоны модели (void) также недопустимы

ВЫВОД РЕЗУЛЬТАТОВ Операторы ELEMENTS и ELOUT – вывод результатов для эйлеровой области TYPE(EUL) = ARCHIVE ELEMENTS(EUL) = 40 SET 40 = ALLEULHYDRO ELOUT(EUL) = XVEL,YVEL,ZVEL,XMOM,YMOM, ZMOM,PRESSURE,ENEGY, DENSITY,SIE,FVUNC TIME(EUL) = 0.0, THRU, END, BY, 1.0E-3 SAVE(EUL) = 100000 Операторы EBDS и EBDOUT – вывод результатов для границы эйлеровой области TYPE(EULB) = TIMEHIS EBDS(EULB) = 16 SETC 16 = FLOW1` EBDOUT(EULD) = MFL,ENERGY,XMOM, FY,MFLR,XVEL TIME(EULB) = 0.0, THRU, END, BY, 1.0E-5 SAVE(EULB) = 100000