Презентация на тему: MSC.Dytran - 08

СОДЕРЖАНИЕ Задание (описание) материалов Уравнение состояния Модели сдвиговых свойств Модели текучести (предельного состояния) Модель нарушения сплошности материала (модель “разрыва”) Модели разрушения

“ТИПЫ” МАТЕРИАЛОВ Операторы задания лагранжевых элементов ссылаются на операторы описания свойств, которые “переадресуют” ссылку на оператор описания материалов CQUAD4,71,100,1,2,3,4 PSHELL,100,300,0.1 DMATEP,300,7852.,210.E9,0.3 Доступны следующие модели материалов: DMAT – “обобщённая” модель материала Материал с комплексным заданием всех свойств, включая текучесть, разрушение, нарушение сплошности (разрыв) Может использоваться для описания только объёмных элементов MAT1 – упругий (эластичный) материал Линейно-упругий материал для моделирования балок и оболочек DMATEL – упругий (эластичный) материал Линейно-упругий материал для моделирования мембран и объёмных тел DMATEP – упруго-пластичный материал с разрушением Линейно упругий и линейно-пластичный материал для моделирования балок и оболочек

“ТИПЫ” МАТЕРИАЛОВ MAT8 + MAT8A – ортотропные материалы, в том числе с разрушением Ортотропные материалы для моделирования оболочек (включая композитные) SHEETMAT – анизотропный упруго-пластичный материал с разрушением для оболочек Используется для моделирования конструкций из металлического листа, полученного прокаткой. Модель разработана проф. Раймондом Крейгом (Raymond Krieg) DMATOR – ортотропный линейно-упругий материал с разрушением Ортотропный материал для моделирования объёмных элементов (в том числе из композиционных материалов) DYMAT14 – материал для моделирования грунтов и вспененных материалов Нелинейный материал с возможностью большого объёмного сжатия и упруго-пластический при деформациях сдвига DYMAT24 – упруго-пластический материал с разрушением Нелинейный упруго-пластический материал с изотропным упрочнением и кусочно-линейной зависимостью напряжения от деформации. Применим для моделирования оболочек, балок и для лагранжевых объёмных элементов

“ТИПЫ” МАТЕРИАЛОВ DYMAT25 – модель материала со специальной зависимостью кинематического упрочнения Материал может использоваться для моделирования структур из камня, бетона и грунта DYMAT26 – ортотропный материал с возможностью большого объёмного сжатия Материал может использоваться только для лагранжевых объёмных элементов RUBBER1 – резиноподобный материал Почти несжимаемый гиперэластичный материал. Может применяться только для лагранжевых объёмных элементов FOAM1 – изотропный материал с возможностью большого сжатия Материал с нулевым значением коэффициента Пуассона FOAM2 – изотропный “пеноподобный” материал с гистерезисом Форма “петли” материала задаётся пользователем, а коэффициент Пуассона имеет нулевое значение

“ПРИМЕНИМОСТЬ” МАТЕРИАЛОВ ДЛЯ РАЗЛИЧНЫХ ЭЛЕМЕНТОВ Балки MAT1 – упругий (эластичный) материал DMATEP - упруго-пластичный материал с разрушением DYMAT24 - упруго-пластический материал с разрушением Оболочки MAT1 – упругий (эластичный) материал DMATEP – упруго-пластичный материал с разрушением MAT8 и MAT8A – ортотропные материалы, в том числе с разрушением SHEETMAT – анизотропный упруго-пластичный материал DYMAT24 – упруго-пластический материал с разрушением Мембраны DMATEL - упругий (эластичный) материал

“ПРИМЕНИМОСТЬ” МАТЕРИАЛОВ ДЛЯ РАЗЛИЧНЫХ ЭЛЕМЕНТОВ Объёмные элементы DMAT – “обобщённая” модель материала DMATEL - упругий (эластичный) материал DMATOR - ортотропный линейно-упругий материал с разрушением DYMAT14 -материал для моделирования грунтов и вспененных материалов DYMAT24 - упруго-пластический материал с разрушением DYMAT25 - модель материала со специальной зависимостью кинематического упрочнения DYMAT26 - ортотропный материал с возможностью большого объёмного сжатия RUBBER1 - резиноподобный материал FOAM1 - изотропный материал с возможностью большого сжатия FOAM2 - изотропный “пеноподобный” материал с гистерезисом

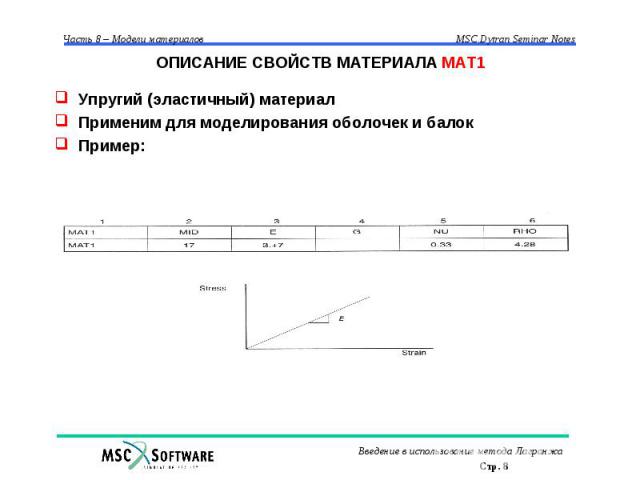
ОПИСАНИЕ СВОЙСТВ МАТЕРИАЛА MAT1 Упругий (эластичный) материал Применим для моделирования оболочек и балок Пример:

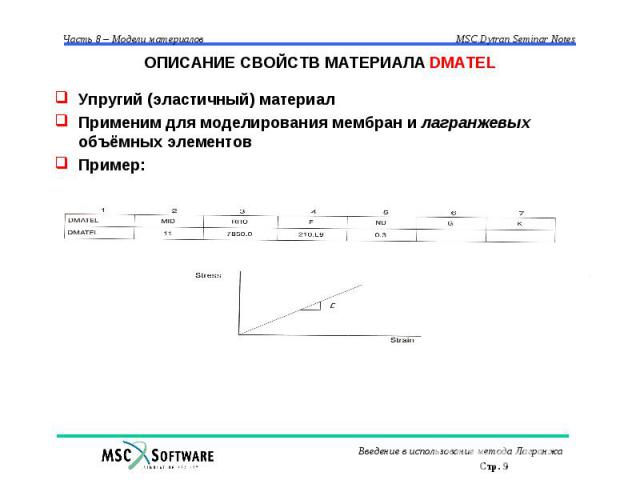
ОПИСАНИЕ СВОЙСТВ МАТЕРИАЛА DMATEL Упругий (эластичный) материал Применим для моделирования мембран и лагранжевых объёмных элементов Пример:

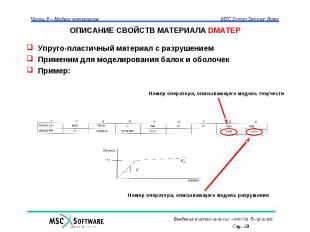
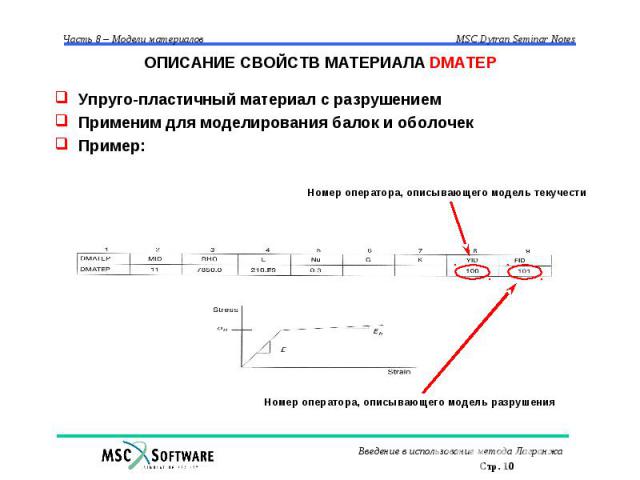
ОПИСАНИЕ СВОЙСТВ МАТЕРИАЛА DMATEP Упруго-пластичный материал с разрушением Применим для моделирования балок и оболочек Пример:

ОПИСАНИЕ СВОЙСТВ МАТЕРИАЛОВ MAT8 И MAT8A Линейно упругий ортотропный материал (MAT8A - с разрушением) Применим для моделирования композиционных материалов Применим только для оболочек Пример: Модели разрушения (для материала MAT8A): Модель Tsai-Hill Модель Tsai-Wu Модифицированная модель Tsai-Wu Модель “максимума напряжения” Модель Chang-Chang Модель пользователя

ОПИСАНИЕ СВОЙСТВ МАТЕРИАЛА SHEETMAT Ортотропный упруго-пластичный материал с разрушением Применяется для моделирования конструкций из металлического листа, полученного прокаткой Разработан проф. Раймондом Крейгом (Raymond Krieg) из университета штата Теннеси (США) Применим только для оболочек

ПРИМЕР: МОДЕЛИРОВАНИЕ ШТАМПОВКИ КОРПУСА АВТОМОБИЛЬНОЙ ФАРЫ С ПОМОЩЬЮ MSC.Dytran

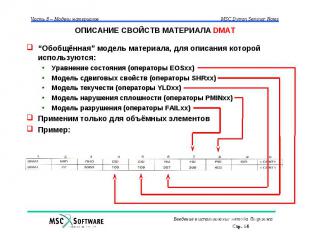
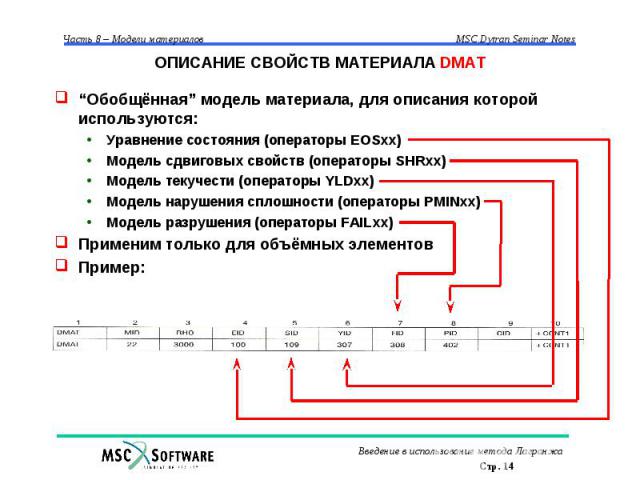
ОПИСАНИЕ СВОЙСТВ МАТЕРИАЛА DMAT “Обобщённая” модель материала, для описания которой используются: Уравнение состояния (операторы EOSxx) Модель сдвиговых свойств (операторы SHRxx) Модель текучести (операторы YLDxx) Модель нарушения сплошности (операторы PMINxx) Модель разрушения (операторы FAILxx) Применим только для объёмных элементов Пример:

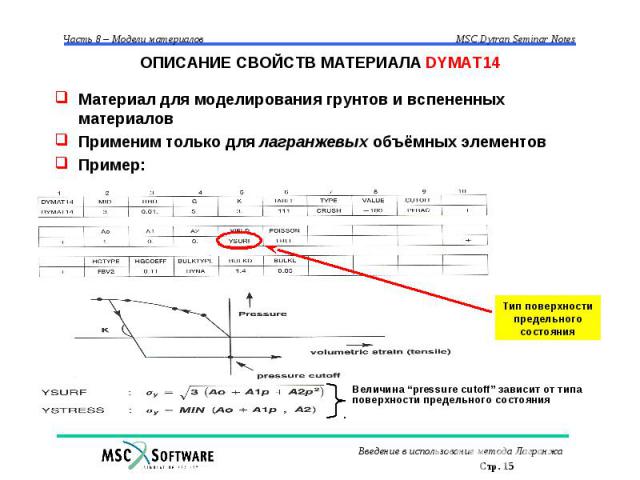
ОПИСАНИЕ СВОЙСТВ МАТЕРИАЛА DYMAT14 Материал для моделирования грунтов и вспененных материалов Применим только для лагранжевых объёмных элементов Пример:

ОПИСАНИЕ СВОЙСТВ МАТЕРИАЛА DYMAT24 Нелинейный упруго-пластический материал с изотропным упрочнением и кусочно-линейной зависимостью напряжения от деформации Возможно моделирование разрушения Применим для моделирования балок, оболочек, для объёмных элементов Пример:

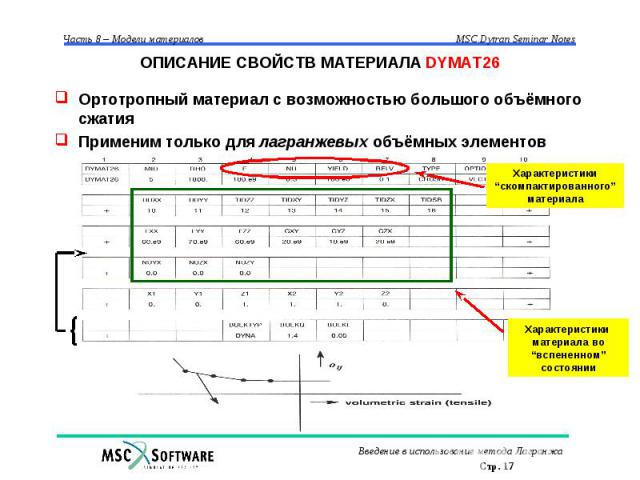
ОПИСАНИЕ СВОЙСТВ МАТЕРИАЛА DYMAT26 Ортотропный материал с возможностью большого объёмного сжатия Применим только для лагранжевых объёмных элементов

ОПИСАНИЕ СВОЙСТВ МАТЕРИАЛА FOAM1 Изотропный материал с возможностью большого сжатия и нулевым значением коэффициента Пуассона. Подходит для моделирования полипропилена Пригоден только для лагранжевых объёмных элементов Пример: задаётся модуль сдвига (G) или объёмный модуль (K)

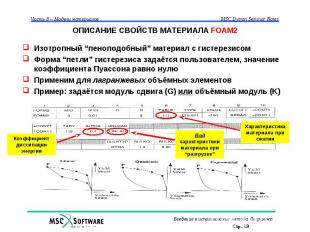
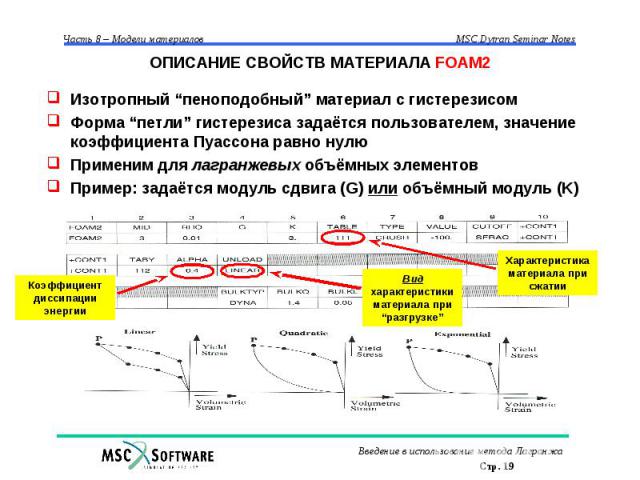
ОПИСАНИЕ СВОЙСТВ МАТЕРИАЛА FOAM2 Изотропный “пеноподобный” материал с гистерезисом Форма “петли” гистерезиса задаётся пользователем, значение коэффициента Пуассона равно нулю Применим для лагранжевых объёмных элементов Пример: задаётся модуль сдвига (G) или объёмный модуль (K)

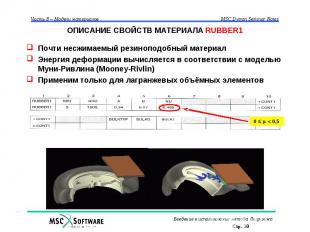
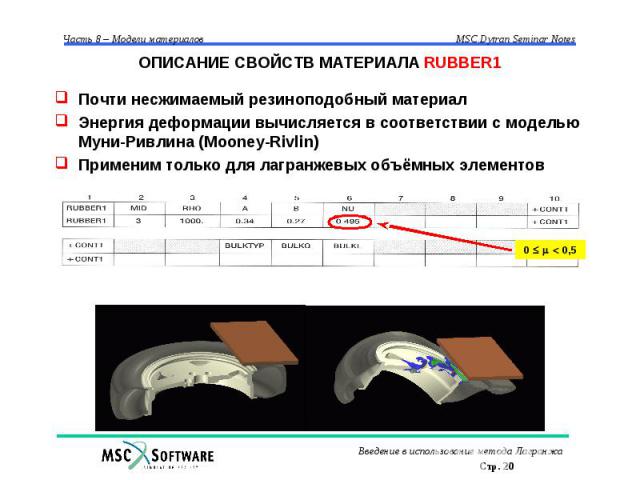
ОПИСАНИЕ СВОЙСТВ МАТЕРИАЛА RUBBER1 Почти несжимаемый резиноподобный материал Энергия деформации вычисляется в соответствии с моделью Муни-Ривлина (Mooney-Rivlin) Применим только для лагранжевых объёмных элементов

УРАВНЕНИЯ СОСТОЯНИЯ Уравнения состояния определяют зависимость давления в материале от изменения его относительного объёма EOSGAM – уравнение состояния идеального газа (адиабатический закон) p = ( - 1) E, где p – давление; – газовая постоянная; – “текущая” плотность материала; E – удельная внутренняя энергия вещества

УРАВНЕНИЯ СОСТОЯНИЯ EOSPOL – полиномиальное уравнение состояния: давление – степенная функция плотности и внутренней энергии вещества При сжатии ( 0): p = a1 + a2 2 + a3 3 + (b0 + b1 + b2 2 + b3 3) E, При растяжении ( 0): p = a1 + (b0 + b1 ) E, где p – давление; = / 0 –1; – “текущая” плотность материала; 0 – плотность материала в “исходном” состоянии; E – удельная внутренняя энергия вещества; ai , bi – коэффициенты

УРАВНЕНИЯ СОСТОЯНИЯ EOSTAIT – уравнение состояния, описывающее модель кавитации Тэта (Tait cavitation model) При отсутствии кавитации ( c): p = a0 + a1( - 1), При наличии кавитации ( c): p = pc, где p – давление; = / 0; – постоянная; – “текущая” плотность материала; 0 – плотность материала в “исходном” состоянии; 0; – “критическое” значение плотности вещества – “порог” кавитации

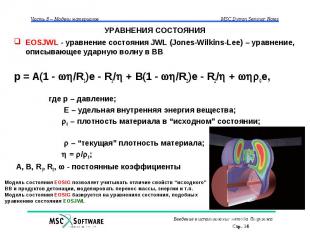
УРАВНЕНИЯ СОСТОЯНИЯ EOSJWL - уравнение состояния JWL (Jones-Wilkins-Lee) – уравнение, описывающее ударную волну в ВВ p = A(1 - /R1)e - R1/ + B(1 - /R2)e - R2/ + 0e, где p – давление; E – удельная внутренняя энергия вещества; 0 – плотность материала в “исходном” состоянии; – “текущая” плотность материала; = / 0; A, B, R1, R2, - постоянные коэффициенты

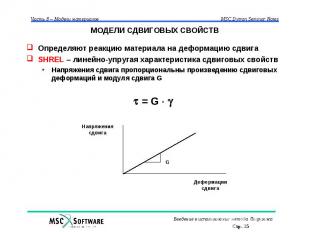
МОДЕЛИ СДВИГОВЫХ СВОЙСТВ Определяют реакцию материала на деформацию сдвига SHREL – линейно-упругая характеристика сдвиговых свойств Напряжения сдвига пропорциональны произведению сдвиговых деформаций и модуля сдвига G = G

МОДЕЛИ СДВИГОВЫХ СВОЙСТВ SHRLVE – изотропная, линейная вязко-упругая модель сдвиговых свойств Механический аналог модели SHRLVE – совокупность соединённых параллельно пружины, вязкого демпфера и элемента Максвелла G0 – “краткосрочный” модуль сдвига G – “долгосрочный” модуль сдвига - коэффициент поглощения элемента Максвелла 0 – коэффициент поглощения сдвиговых деформаций

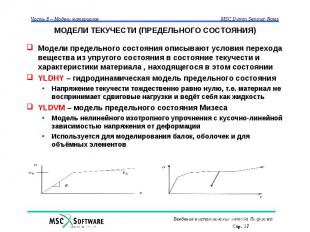
МОДЕЛИ ТЕКУЧЕСТИ (ПРЕДЕЛЬНОГО СОСТОЯНИЯ) Модели предельного состояния описывают условия перехода вещества из упругого состояния в состояние текучести и характеристики материала , находящегося в этом состоянии YLDHY – гидродинамическая модель предельного состояния Напряжение текучести тождественно равно нулю, т.е. материал не воспринимает сдвиговые нагрузки и ведёт себя как жидкость YLDVM – модель предельного состояния Мизеса Модель нелинейного изотропного упрочнения с кусочно-линейной зависимостью напряжения от деформации Используется для моделирования балок, оболочек и для объёмных элементов

МОДЕЛИ ТЕКУЧЕСТИ (ПРЕДЕЛЬНОГО СОСТОЯНИЯ) YLDJC – модель предельного состояния Johnson-Cook’а y = (A + B p) · 1 + C ln( / 0) {1 - (T-Tr)/(Tm-Tr) m}, где p – “текущее” значение пластической деформации; – “текущее” значение “скорости” деформации; 0 – параметр; Т – температура; Tr – температура окружающей среды; Tm – температура плавления вещества; A, B, n, C, m – постоянные коэффициенты YLDMC – модель текучести Мора-Кулона (Mohr-Coulomb) – применима только для эйлеровых материалов, воспринимающих сдвиговую нагрузку y = min (Y1, Y2 + Y3 p), где Y1, Y2, Y3 – константы; p – давление

МОДЕЛЬ НАРУШЕНИЯ СПЛОШНОСТИ Определяет минимальное значение давления, при котором нарушается сплошность материала - возникает разрыв PMINC – напряжение нарушения сплошности постоянно

МОДЕЛИ РАЗРУШЕНИЯ Определяют условия разрушения материала (после которого элемент в вычислениях “не участвует”) FAILMPS – задаётся уровень эквивалентных деформаций, при котором наступает (вязкое) разрушение материала FAILEXn – модели разрушения, определяемые пользовательскими подпрограммами (FAILEX – мгновенное разрушение, FAILEX1 – возможность постепенной деградации свойств материала DMATOR) FAILEST – разрушение при достижении эквивалентным напряжением определённого уровня (при этом происходит потеря возможности восприятия элементом сдвиговых нагрузок, “гидродинамические” свойства сохраняются) и при уменьшении шага интегрирования ниже определённого предела (после этого происходит “полное” разрушение элемента) – модель двухэтапного разрушения

МОДЕЛИ РАЗРУШЕНИЯ FAILMES – разрушение при достижении эквивалентным напряжением заданного предельного уровня FAILPRS – разрушение при достижении гидродинамическим давлением заданного максимального уровня FAILSDT - разрушение при достижении эквивалентными пластическими деформациями определённого уровня (при этом происходит потеря возможности восприятия элементом сдвиговых нагрузок, “гидродинамические” свойства сохраняются) и при уменьшении шага интегрирования ниже определённого предела (после этого происходит “полное” разрушение элемента) – модель двухэтапного разрушения

ПРИМЕР ОПИСАНИЯ СВОЙСТВ МАТЕРИАЛА Пример описания свойств стали (материал № 333) со следующими свойствами: Плотность 7830 кг/м3 Объёмный модуль 1,69 1011 Н/м2 Модуль сдвига 8,18 1010 Н/м2 Предел текучести 5,0 108 Н/м2 Напряжение нарушения сплошности (“разрыва”) - 3,8 109 Н/м2 Условие разрушения – достижение 50%-ой пластической деформации DMAT, 333, 7830., 444, 555, 666, 777, 888 EOSPOL, 444, 1.69E11 SHREL, 555, 9.18E10 YLDVM, 666, 5.E8 FAILMPS, 777, 0.5 PMINC, 888, -3.8E9