Презентация на тему: MSC.Dytran - 02

СОДЕРЖАНИЕ Технология решения явным методом Шаг интегрирования при явном методе Сравнение явного и неявного методов решения Границы применимости явного метода интегрирования

ТЕХНОЛОГИЯ РЕШЕНИЯ ЯВНЫМ МЕТОДОМ Основы технологии Решение задачи в пространстве – методом конечных элементов и/или методом конечных объёмов Решение задачи во времени – явным методом интегрирования - большое количество небольших шагов по времени Использование в MSC.Dytran Решение задачи в пространстве Моделирование конструкции - решатель Лагранжа – метод конечных элементов Моделирование жидкости (газа) – решатель Эйлера – метод конечных объёмов Решение задачи во временной области – интегрирование по методу центральных разностей

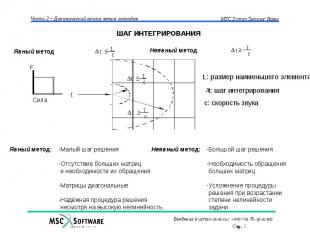
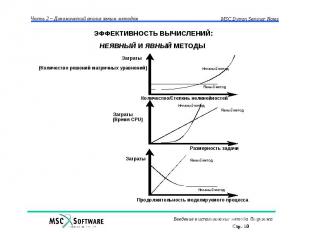
НЕЯВНЫЙ И ЯВНЫЙ МЕТОДЫ ИНТЕГРИРОВАНИЯ Неявный метод интегрирования M · a´n+1 + C · v´n+1 + K · d´n+1 = Fextn+1 [M + C · · t + K · · t2] · a´n+1 = Fextn+1 - C · v*n - K · d*n Fresidial = Fext - Fint a´n+1 = [M*]-1 · Fresidialn+1 Явный метод интегрирования M · an + C · vn + K · dn = Fextn an = [M]-1 · Fresidialn