Презентация на тему: MSC.Dytran - 05

СОДЕРЖАНИЕ Основные положения Дискретизация массы Вычислительный цикл Явная схема интегрирования Вычисление напряжений и сил

ОСНОВНЫЕ ПОЛОЖЕНИЯ Дискретизация пространственного объекта с помощью конечных элементов Объёмные (3D) элементы Оболочечные (2D) элементы Стержневые (1D) элементы Дискретные элементы – пружины, демпферы и жёсткие тела Сетка “скреплена” с материалом и движется вместе с ним; элементы деформируются при деформировании материала Лагранжевы элементы имеют неизменную массу Конечные элементы сопрягаются друг с другом посредством общих узлов Скорость движения материала определяется скоростью движения узлов Силы прилагаются к узлам Напряжения определяются (вычисляются) в центре элемента

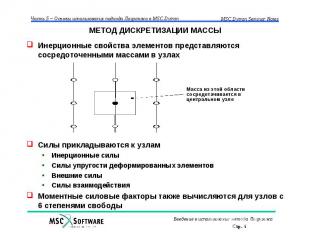
МЕТОД ДИСКРЕТИЗАЦИИ МАССЫ Инерционные свойства элементов представляются сосредоточенными массами в узлах Силы прикладываются к узлам Инерционные силы Силы упругости деформированных элементов Внешние силы Силы взаимодействия Моментные силовые факторы также вычисляются для узлов с 6 степенями свободы

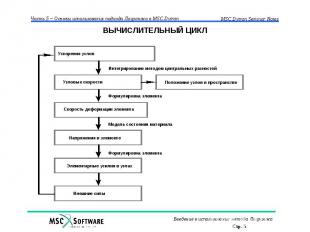
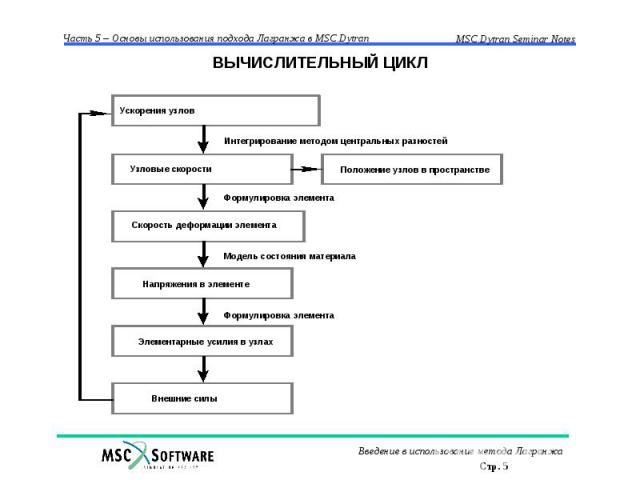
ВЫЧИСЛИТЕЛЬНЫЙ ЦИКЛ

ЯВНАЯ СХЕМА ИНТЕГРИРОВАНИЯ Ускорение узлов вычисляется по формуле M · an = Fext - Fint где M – матрица масс; Fext – внешние нагрузки; Fint – внутренние силы, “генерируемые” элементами Матрица M – диагональная Нет необходимости в обращении матриц, т.к. уравнения независимы: an =(Fext - Fint)/m где m – масса, относящаяся к узлу “Продвижение” во времени выполняется с использованием метода центральных разностей Вычисляются скорости узлов в момент времени n+1/2 Vn+1/2 = Vn-1/2 + an ( tn+1/2 + tn-1/2)/2 Вычисляются координаты узлов в момент времени n+1 dn+1 = dn + Vn+1/2 tn+1/2

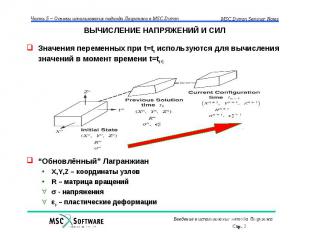
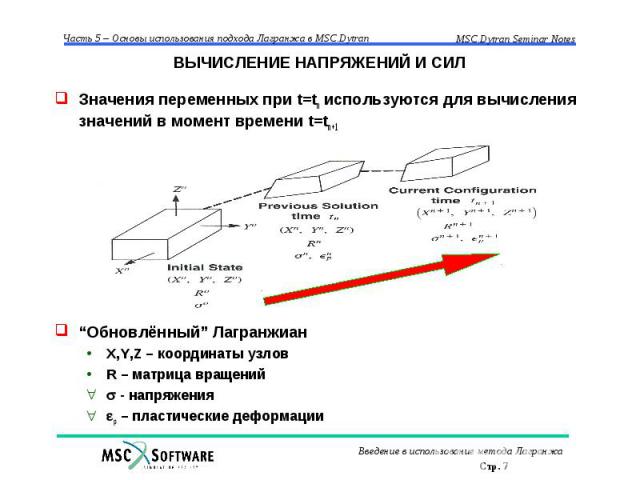
ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ И СИЛ Значения переменных при t=tn используются для вычисления значений в момент времени t=tn+1 “Обновлённый” Лагранжиан X,Y,Z – координаты узлов R – матрица вращений - напряжения p – пластические деформации

ВЫЧИСЛЕНИЕ НАПРЯЖЕНИЙ И СИЛ Вычисляются координаты (при tn+1) и скорости (при tn+1/2) С использованием скоростей узлов при tn+1/2 вычисляется скорость изменения деформаций С использованием скорости изменения деформаций вычисляется приращение величины деформаций Выполняется корректировка составляющих напряжений ( n), учитывающая поворот элемента как твёрдого тела вместе с поворотом подвижной системы координат С использованием инкрементов деформаций в подвижной системе координат и модели состояния материала вычисляются приращения напряжений n+1/2 Суммируя “откорректированные” (с учётом поворота подвижной системы координат) напряжения и их приращения, вычисляют напряжения при t= tn+1 n+1 = nrotated + n+1/2 С использованием “новых” значений напряжений вычисляются внутренние силы в узлах