Презентация на тему: MSC.Dytran - 07

СОДЕРЖАНИЕ Назначение и типы элементов Описание элемента Координатные системы Объёмные элементы Оболочечные элементы Балочные и стержневые элементы Пружины и демпферы Пружины Демпферы Сосредоточенные массы

НАЗНАЧЕНИЕ И ТИПЫ ЭЛЕМЕНТОВ Назначение: используются для построения расчётных моделей Типы элементов: Объёмные Четырёхугольные оболочки Треугольные оболочки Треугольные мембраны Балки Стержни Пружины и демпферы Сосредоточенные массы Жёсткие тела

ОПИСАНИЕ ЭЛЕМЕНТА Для описания элемента необходимо задать: Координаты узлов – задаются оператором GRID Топологию элемента – задаётся оператором Cxx Свойства элемента (математическую формулировку) – задаётся оператором Pxx Материал – тип материала и его параметры задаются операторами DMATxx, DYMATxx или MATxx Каждый оператор должен иметь свой уникальный номер (ID). На этот номер (например, на номер оператора, описывающего свойство элемента, свойство материала и т.п.) можно ссылаться любое количество раз

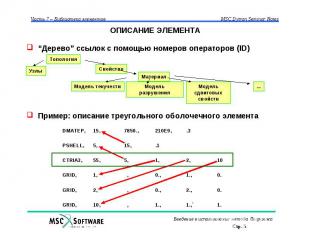
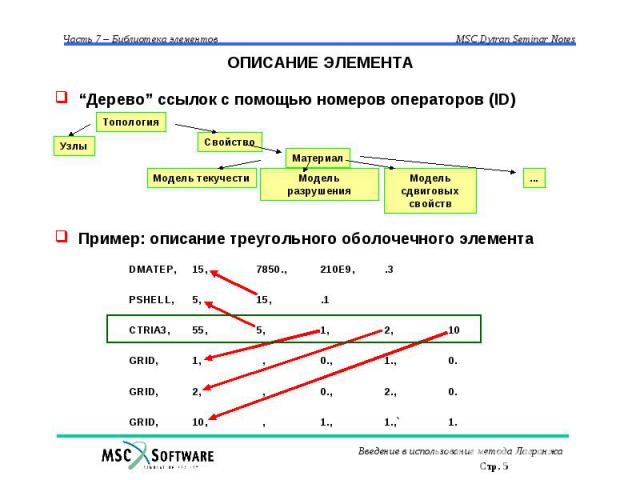
ОПИСАНИЕ ЭЛЕМЕНТА “Дерево” ссылок с помощью номеров операторов (ID) Пример: описание треугольного оболочечного элемента

СИСТЕМЫ КООРДИНАТ Основная (глобальная) система координат Это прямоугольная система координат (система координат № 0) используется по умолчанию. Все другие системы координат в конечном счёте определяются (задаются) по отношению к этой основной системе координат Конфигурация элементов (по умолчанию) задаётся в основной системе координат Вычисления выполняются в локальной системе координат элемента Результаты расчётов по умолчанию представляются в основной системе координат Локальная координатная система Расположение узлов может задаваться в локальной координатной системе, определяемой пользователем Закрепления и нагрузки также могут задаваться в локальных системах координат Типы координатных систем Прямоугольная (x, y, z) Цилиндрическая (R, , Z) Сферическая (R, , )

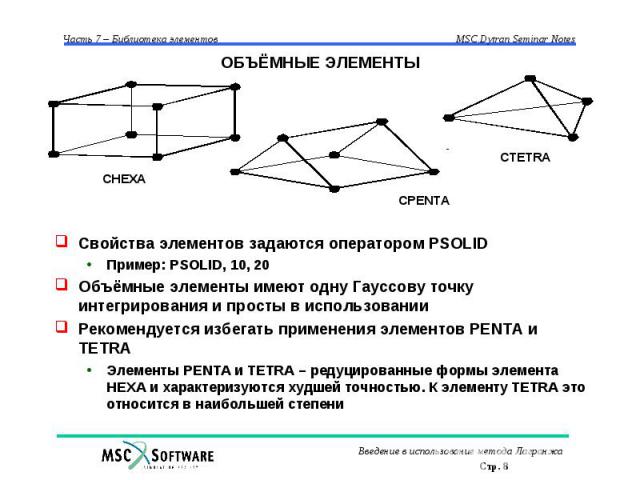
ОБЪЁМНЫЕ ЭЛЕМЕНТЫ Используются для моделирования объёмных частей конструкции Базируются на 8-ми узлах (гексагональные элементы) Элементы PENTA и TETRA – редуцированные варианты восьми узлового элемента HEXA Уравнения, описывающие объёмные элементы, включают только три степени свободы узлов, сопряжённых с данными элементами Для лагранжевых объёмных элементов с ортотропными материалами вычисления ведутся в локальной системе координат

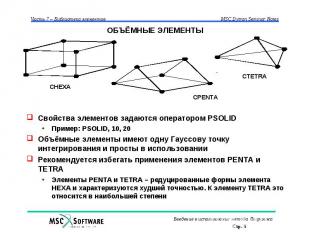
ОБЪЁМНЫЕ ЭЛЕМЕНТЫ Свойства элементов задаются оператором PSOLID Пример: PSOLID, 10, 20 Объёмные элементы имеют одну Гауссову точку интегрирования и просты в использовании Рекомендуется избегать применения элементов PENTA и TETRA Элементы PENTA и TETRA – редуцированные формы элемента HEXA и характеризуются худшей точностью. К элементу TETRA это относится в наибольшей степени

ЗАДАНИЕ “СОЛИДНОЙ ГЕОМЕТРИИ” Для описания “солидной геометрии” используются операторы GRID CHEXA PSOLID Пример описания объёмного лагранжева элемента 71 со свойством 100 и материалом 200 GRID, 1, , 0., 0., 0. GRID, 2, , 1., 0., 0. …описание узлов с 3-го по 8-ой… CHEXA, 71, 100, 1, 2, 3, 4, 5, 6, + +, 7, 8 PSOLID, 100, 200

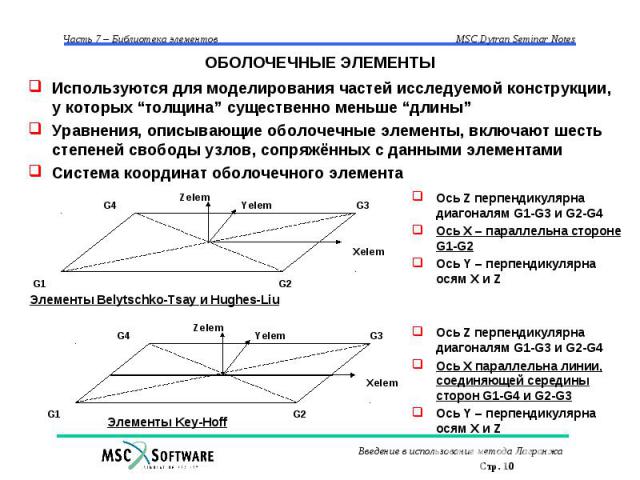
ОБОЛОЧЕЧНЫЕ ЭЛЕМЕНТЫ Используются для моделирования частей исследуемой конструкции, у которых “толщина” существенно меньше “длины” Уравнения, описывающие оболочечные элементы, включают шесть степеней свободы узлов, сопряжённых с данными элементами Система координат оболочечного элемента

ОБОЛОЧЕЧНЫЕ ЭЛЕМЕНТЫ Элемент CQUAD4 Элемент Belytschko-Tsay Элемент базируется на оболочечной формулировке C0-Mindlin, имеет одну точку интегрирования и характеризуется постоянной величиной деформации Очень эффективный элемент, позволяет получать хорошие результаты при больших изгибных деформациях Предполагается, что элемент имеет плоскую форму и при “короблении” элемента результаты могут быть неточными Толщина элемента постоянна по всей его плоскости Пример задания свойства элемента Belytschko-Tsay PSHELL1, 10, 20, BLT, , , , , , + +, 0.8

ОБОЛОЧЕЧНЫЕ ЭЛЕМЕНТЫ Элемент CQUAD4 Элемент Hughes-Liu Элемент базируется на оболочечной формулировке C0-Mindlin, имеет одну точку интегрирования и характеризуется постоянной величиной деформации Более сложный и более вычислительно затратный по сравнению с элементом Belytschko-Tsay Элемент может быть “неплоским”, однако при “короблении” элемента точность результатов может снижаться Толщина по площади элемента может быть неравномерной Особенно рекомендуется применять в случае использования упруго-пластической модели материала с разрушением Пример задания свойства элемента Hughes-Liu PSHELL1, 10, 20, HUGHES, , , , , , + +, 0.8

ОБОЛОЧЕЧНЫЕ ЭЛЕМЕНТЫ Элемент CQUAD4 Элемент Key-Hoff Элемент подобен элементу Belytschko-Tsay, но с некоторыми улучшениями Допускается неплоскостность геометрии Опция “сдвиговая жёсткость” обеспечивает учёт физически обоснованной жёсткости “коробления” Высокая точность результатов при очень больших деформациях изгиба и при “короблении” Не требуется контролировать бездеформационные моды деформации (деформации типа “песочные часы”) при “короблении” элементов Примерно в два раза более вычислительно затратен по сравнению элементом Belytschko-Tsay Пример задания свойства элемента Key-Hoff PSHELL1, 10, 20, KEYHOFF, , , , , , + +, 0.8 При использовании оператора PSHELL для элементов CQUAD4 подразумевается формулировка Key-Hoff PSHELL, 10, 20, 0.1

ОБОЛОЧЕЧНЫЕ ЭЛЕМЕНТЫ Элемент CTRIA3 Элемент C0-triangle Эффективный трёхузловой элемент, даёт хорошие результаты при изгибных деформациях. Этот элемент “жёстче”, чем четырёхузловой элемент и вследствие этого должен применяться только в “переходных” зонах или в задачах с преобладанием изгибных деформаций Пример задания свойства элемента CTRIA3 PSHELL1, 10, 20, C0-TRIA, , , , , , + +, 0.8 При использовании оператора PSHELL для элементов CTRIA3 предполагается формулировка C0-triangle PSHELL, 10, 20, 0.8 Элемент – мембрана Пример описания свойств элемента – мембраны (элемент не “сопротивляется” изгибу) PSHELL1, 10, 20, MEMB, , , , , , + +, 0.8

ЗАДАНИЕ “ОБОЛОЧЕЧНОЙ ГЕОМЕТРИИ” Для описания “оболочечной геометрии” используются операторы GRID CQUAD / CTRIA PSHELL / PSHELL1 / PCOMP Пример описания оболочечного элемента 71 (формулировка Belytschko-Tsay) со свойством 100 (толщина 0,1) и материалом 200 GRID, 1, , 0., 0., 0. GRID, 2, , 1., 0., 0. GRID, 3, , 0., 1., 0. GRID, 4, , 1., 1., 0. CQUAD4, 71, 100, 1, 2, 3, 4 PSHELL1, 100, 200, BLT, , , , , , + +, 0.1

БАЛОЧНЫЕ ЭЛЕМЕНТЫ Используются для моделирования протяжённых компонентов Элемент-балка сопрягается с двумя узлами (элемент 1D) Уравнения, описывающие балочные элементы, включают шесть степеней свободы узлов, сопряжённых с данными элементами Система координат элемента-балки Ось X проходит через узлы G1 и G2 Положение плоскости XY определяется внешним узлом G3; ось Y перпендикулярна оси X Ось Z перпендикулярна осям X и Y

БАЛОЧНЫЕ ЭЛЕМЕНТЫ Элементы CBAR и CBEAM Элемент Belytschko-Schwer (формулировка “по умолчанию”) Эффективный балочный элемент, основанный на модели“обобщённой” пластичности: всё сечение балки одновременно переходит в состояние пластичности (это неприемлемо в случае важности точного моделирования “частично” пластического состояния балки) Линейная зависимость изгибающего момента: переход в пластическое состояние может происходить на любом из концов В отличие от MSC.Nastran, в MSC.Dytran нет разницы в формулировках между элементами CBAR и CBEAM

БАЛОЧНЫЕ ЭЛЕМЕНТЫ Описание свойств балочных элементов Необходимо задание следующих свойств балочного элемента Площадь поперечного сечения: A Моменты инерции поперечного сечения: Iyy, Izz Полярный момент инерции поперечного сечения: J Модули пластичности: Zy, Zz (только, если необходимо моделировать текучесть) Пример задания свойств элемента-балки: PBAR, 10, 20, 49.3, 10054.0, 333.0, 5193.0 PBEAM1, 10, 20, BELY, , , , , + +, 49.3, 10054.0, 333.0, 5193.0, 651.8, 85.07 В примере с оператором PBEAM1 моделирование пластического состояния балки будет выполняться в предположении прямоугольной формы её сечения (параметр, определяющий форму сечения, имеет значение, принятое “по умолчанию”, т.е. RECT - прямоугольник)

БАЛОЧНЫЕ ЭЛЕМЕНТЫ Элементы CBAR и CBEAM Элемент Hughes-Liu – модель “частичной” пластичности Вычислительно более затратный (по сравнению с элементом Belytschko-Schwer), но обеспечивает моделирование пластического состояния части сечения и применение сложных моделей материала. Рекомендуется применять только при необходимости использования вышеуказанных возможностей Изгибающий момент постоянен по длине элемента Задаётся форма и размеры поперечного сечения элемента Пример задания свойств элемента с прямоугольным сечением 200 мм 100 мм (Внимание: новый формат оператора!): PBEAM1, 10, 20, HLSECTS, DYTRAN, , , TSECT, , + +, 200.0, 100.0, 0.0, 200.

БАЛОЧНЫЕ ЭЛЕМЕНТЫ Элементы CBAR и CBEAM Композитная балка Форма поперечного сечения может быть произвольной, в состав балки могут входить различные материалы Формулировка элемента – Hughes-Liu Свойства элементов-композитных балок задаются оператором PBCOMP Пример задания свойств элемента с прямоугольным сечением (балка из трёх материалов): PBCOMP, 10, 20, 2.9, , , , , , + +, , , , , , , 1, , + +, 0.50, 1.20, 1.0, 18, , , , , + +, 0.20, 0.90, 1.0, 19

БАЛОЧНЫЕ ЭЛЕМЕНТЫ Интегрирование уравнений, описывающих балочные элементы Два алгоритма интегрирования Гаусса (Gauss’а) PBEAM1, 10, 20, HUGHES, GAUSS, , , , , + +, 200.0, 200.0, 100.0, 100.0 Лобатто (Lobatto) PBEAM1, 10, 20, HUGHES, LOBATTO, , , , , + +, 200.0, 200.0, 100.0, 100.0 В версии 2002 это не актуально (формат оператора изменился)

ЭЛЕМЕНТЫ - СТЕРЖНИ Элементы CROD “Работают” только на растяжение-сжатие Высокоэффективный (в вычислительном плане) элемент. Необходимо задать только площадь поперечного сечения Пример задания элемента – стержня: CROD, 1, 10, 2, 3 PROD, 10, 20, 10.73

ЗАДАНИЕ “ГЕОМЕТРИИ” ЭЛЕМЕНТОВ BEAM / ROD Для описания “геометрии” используются операторы GRID CBAR /CBEAM / CROD PBAR / PBEAM / PBEAM1 / PROD Пример описания балочного элемента 71 со свойством 100 и материалом 200 GRID, 1, , 0., 0., 0. GRID, 2, , 1., 0., 0. GRID, 3, , 0., 0., 1. CBEAM, 71, 100, 1, 2, 3 PBEAM, 100, 200, 100., 25., 25., , 30.

ПРУЖИНЫ И ДЕМПФЕРЫ Используются для моделирования частей конструкции, поведение которых “напоминает” поведение пружин и демпферов Элементы “пружины” и “демпферы” сопрягаются с двумя узлами Элементы “пружины” и “демпферы” с линейными и нелинейными характеристиками Пружины, имеющие ориентацию в пространстве – CSPR Скалярные пружины – CELASn Демпферы, имеющие ориентацию в пространстве – CVISC Скалярные демпферы – CDAMPn

ЭЛЕМЕНТЫ - ПРУЖИНЫ CSPR – пружины, имеющие ориентацию в пространстве Элементы CSPR сопрягаются с двумя узлами. Усилие в элементе всегда направлено вдоль прямой, соединяющей узлы, при вращении элемента соответственно поворачивается и направление действия силы CELASn – скалярные пружины CELAS1 и CELAS2 могут сопрягаться с одним или двумя узлами. Направление действия силы задаётся при описании элемента и в дальнейшем не зависит от взаимного положения узлов. Свойства элемента CELAS1 задаются оператором PELASn и могут линейными и нелинейными. Параметры (свойства) элемента CELAS2 указываются непосредственно в операторе, описывающем топологию элемента. Такой элемент может быть только линейным

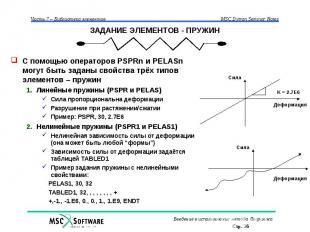
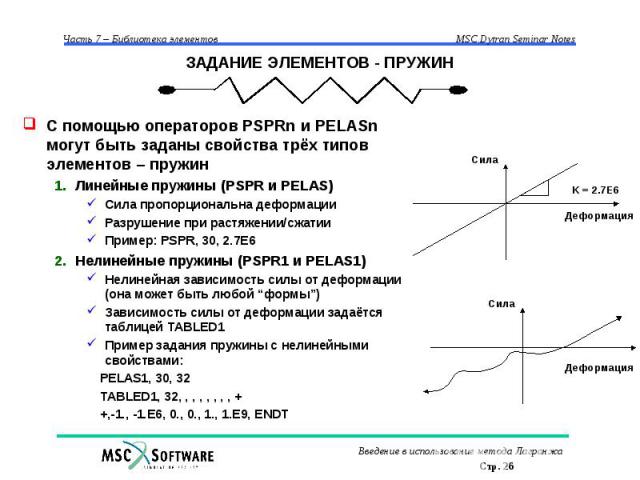
ЗАДАНИЕ ЭЛЕМЕНТОВ - ПРУЖИН С помощью операторов PSPRn и PELASn могут быть заданы свойства трёх типов элементов – пружин Линейные пружины (PSPR и PELAS) Сила пропорциональна деформации Разрушение при растяжении/сжатии Пример: PSPR, 30, 2.7E6 Нелинейные пружины (PSPR1 и PELAS1) Нелинейная зависимость силы от деформации (она может быть любой “формы”) Зависимость силы от деформации задаётся таблицей TABLED1 Пример задания пружины с нелинейными свойствами: PELAS1, 30, 32 TABLED1, 32, , , , , , , , + +,-1., -1.E6, 0., 0., 1., 1.E9, ENDT

ЗАДАНИЕ ЭЛЕМЕНТОВ - ПРУЖИН 3. Свойства пружин, особым образом задаваемые пользователем (PSPREX, PELASEX) Характеристики пружин задаются посредством пользовательских подпрограмм

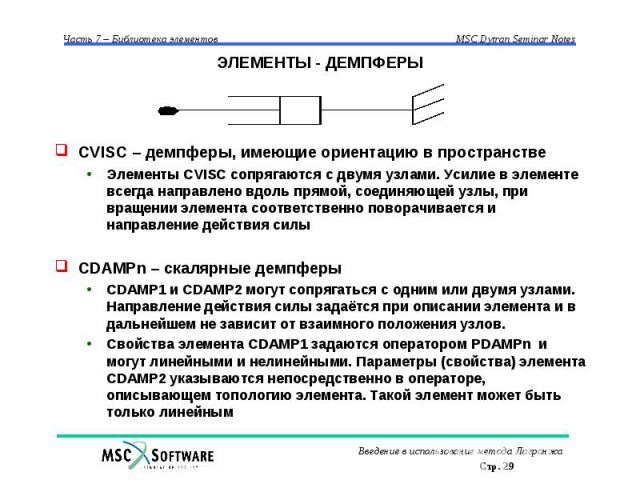
ПРИМЕРЫ ЗАДАНИЯ НЕЛИНЕЙНЫХ ПРУЖИН Моделирование зазора PSPR1, 100, 110 TABLED1, 110, , , , , , , , + +, -1., -1.E6, 0., 0., 1., 0., ENDT Моделирование тросов PSPR1, 30, 32 TABLED1, 32, , , , , , , , + +, -1., 0., 0., 0., 1., 1.E6, ENDT Разрушение компонента конструкции PSPR1, 30, 32 TABLED1, 32, , , , , , , , + +, -1., -1.E6, 1., 1.E6, 1., 0., 2.0, 0., + +, ENDT

ЭЛЕМЕНТЫ - ДЕМПФЕРЫ CVISC – демпферы, имеющие ориентацию в пространстве Элементы CVISC сопрягаются с двумя узлами. Усилие в элементе всегда направлено вдоль прямой, соединяющей узлы, при вращении элемента соответственно поворачивается и направление действия силы CDAMPn – скалярные демпферы CDAMP1 и CDAMP2 могут сопрягаться с одним или двумя узлами. Направление действия силы задаётся при описании элемента и в дальнейшем не зависит от взаимного положения узлов. Свойства элемента CDAMP1 задаются оператором PDAMPn и могут линейными и нелинейными. Параметры (свойства) элемента CDAMP2 указываются непосредственно в операторе, описывающем топологию элемента. Такой элемент может быть только линейным

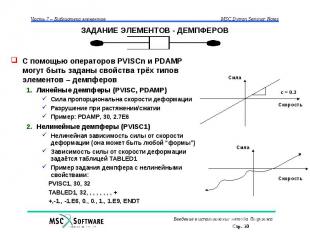
ЗАДАНИЕ ЭЛЕМЕНТОВ - ДЕМПФЕРОВ С помощью операторов PVISCn и PDAMP могут быть заданы свойства трёх типов элементов – демпферов Линейные демпферы (PVISC, PDAMP) Сила пропорциональна скорости деформации Разрушение при растяжении/сжатии Пример: PDAMP, 30, 2.7E6 Нелинейные демпферы (PVISC1) Нелинейная зависимость силы от скорости деформации (она может быть любой “формы”) Зависимость силы от скорости деформации задаётся таблицей TABLED1 Пример задания демпфера с нелинейными свойствами: PVISC1, 30, 32 TABLED1, 32, , , , , , , , + +,-1., -1.E6, 0., 0., 1., 1.E9, ENDT

ЗАДАНИЕ ЭЛЕМЕНТОВ - ДЕМПФЕРОВ 3. Свойства демпферов, особым образом задаваемые пользователем (PVISCEX) Характеристики демпферов задаются посредством пользовательских подпрограмм

ЭЛЕМЕНТЫ – СОСРЕДОТОЧЕННЫЕ МАССЫ Элементы CONM2 Используются для “добавления” массы или инерции узлам лагранжевой сетки Все узлы должны иметь отличную от нуля массу – либо вследствие задания соответствующих свойств элементов, сопрягающихся с данным узлом, либо за счёт использования элемента CONM2 (опять же сопрягаемого с данным узлом) Пример описания элемента CONM2 №7, увеличивающего на 0,1 массу, ассоциированную с узлом 9: CONM2, 7, 9, , 0.1 ПОМНИТЕ: МАССИВНЫЕ СВОЙСТВА В MSC.DYTRAN НАДО ЗАДАВАТЬ ТОЛЬКО В ЕДИНИЦАХ МАССЫ (И НИ В КОЕМ СЛУЧАЕ НЕ В ЕДИНИЦАХ ВЕСА)!!!!

РАСПРОСТРАНЁННЫЕ ПРОБЛЕМЫ Использование клавиши TAB при создании входного файла