Презентация на тему: MSC.Dytran - 14


СОДЕРЖАНИЕ Основные положения метода Эйлера Основы метода конечных объёмов Цикл вычислений Критерий Куранта

ОСНОВНЫЕ ПОЛОЖЕНИЯ МЕТОДА ЭЙЛЕРА Дискретизация исследуемой области с использованием объёмных элементов Сетка неподвижна в пространстве Объём элементов постоянен Узлы сетки не имеют степеней свободы Материал перемещается (“течёт”) от одного элемента к другому

УРАВНЕНИЯ, ОПИСЫВАЮЩИЕ ЭЙЛЕРОВУ СРЕДУ Поведение материала в эйлеровой части модели описывается 4-мя уравнениями состояния V(P,t) – скорость течения материала в точке P в момент времени t (P,t) – плотность материала в точке P в момент времени t e(P,t) – удельная внутренняя энергия материала в точке P в момент времени t ij(P,t) – напряжения в материале в точке P в момент времени t Эти уравнения обеспечивают выполнение основных физических законов: Уравнение непрерывности – закон сохранения массы Уравнение для количества движения – 2-ой закон динамики (Ньютона) Уравнение для энергии – 1-ое начало термодинамики Уравнение состояния Уравнение состояния: p=f( ,e) Связь между напряжениями и деформациями Пластичность (текучесть) материала Разрушение

ИСПОЛЬЗОВАНИЕ ПОДХОДА ЭЙЛЕРА В MSC.Dytran Метод конечных объёмов В пространственной области решение основано на методе конечных объёмов Интегрирование по времени Во временной области решение основано на использовании метода центральных разностей и явной схеме интегрирования Аналогичный метод решения во временной области применяется и для вычислений с лагранжевой частью расчётной модели

ОСНОВЫ МЕТОДА КОНЕЧНЫХ ОБЪЁМОВ Элементы эйлеровой части модели рассматриваются в качестве конечных объёмов Масса, скорость, внутренняя энергия и напряжения определяются для центра элемента и эти значения распространяются на весь элемент

ПРЕИМУЩЕСТВА МЕТОДА КОНЕЧНЫХ ОБЪЁМОВ Возможно моделирование очень больших деформаций – материал как-бы течёт внутри эйлеровой сетки Исключены трудоёмкие операции по построению конечно-элементной сетки Предотвращается уменьшение шага интегрирования до недопустимо малых величин за счёт исключения использования плотной сетки и элементов малого размера

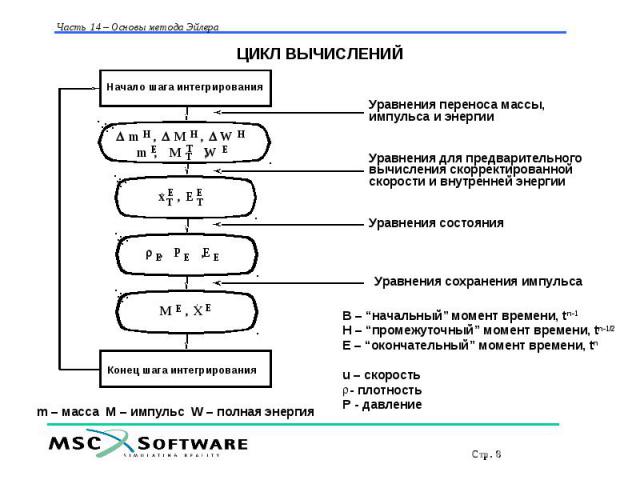
ЦИКЛ ВЫЧИСЛЕНИЙ

ОПРЕДЕЛЕНИЕ ШАГА ИНТЕГРИРОВАНИЯ Шаг интегрирования вычисляется с использованием критерия Куранта Критерий Куранта основан на учёте минимального промежутка времени, необходимого для распространения волны напряжений на расстояние, равное размеру элемента В лагранжевом решателе шаг интегрирования зависит только от скорости звука в материале и наименьшего размера элемента L При определении шага интегрирования в эйлеровом решателе принимается во внимание суперпозиция скорости распространения волны напряжений в материале и скорости перемещения самого материала и, соответственно t = S·L/(u + c), где по умолчанию S = 2/3 Причина этого – “несвязанность” перемещения материала и сетки (в случае же лагранжева решателя сетка перемещается вместе с материалом)