Презентация на тему: Виды и свойства треугольников

5klass.net

А С в

Обеспечить повторение, обобщение и систематизации темы : «Треугольник» 1) Рассмотреть различные виды треугольника и их свойства. 2) Взаимное расположение треугольника и окружности. 3) Различные формулы нахождения элементов треугольника.

- это геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой и отрезков соединяющих эти точки. По сторонам По углам Равнобедренный Равносторонний разносторонний Остроугольный Тупоугольный Прямоугольный

Задача №1. В тупоугольном треугольнике (с тупым углом В) проведите медиану ВМ, биссектрису АD, высоту CH. В С А М D H Задача №2. В треугольнике MPK проведите среднюю линию FS так, что т.F лежит на стороне МP, т.S на МК. M K P S F

Задача №3. По данным рисунка найти DC, Р, S, высоту BH. А В С D 8см 12см 4см ? см AD- биссектриса, по свойству биссектрисы треугольника: ВD:DC=AB:AC, 4:DC=8:12, DC=4*12:8=6(см) Решение: 2) Р=AB+AC+(BD+DC)= =8+12+(4+6)=30(см) H S=1/2*BH*AC BH=2*S:AC=2,5

А В С H Задача №6. По данным рисунка найти высоту AH, sinВ, cosС. 9 см 4 см Решение: 2) sinB= cosC=

Задача №4. F K T O M P N Построение чертежа: В прямоугольный треугольник, с гипотенузой KT=26 см, вписана окружность с радиусом 4см. Найдите катеты, площадь треугольника и длину описанной около него окружности. 1) Треугольник FKT. 2) Вписанная окружность: т.О- пересечение биссектрис; OP,ОM, ON (перпендикуляры проведенные к сторонам треугольника) являются радиусами окружности. 3) Точки P, N, M – точки касания окружности и сторон треугольника.

Задача №4. F K T O M P N Решение: 1) PO=MO=NO=4(см)-как радиусы одной окружности. 2) FPOM-квадрат (смежные стороны равны, углы прямые). FM=PF=4(см) по определению квадрата. 3) PK=КN=x(см) по свойству отрезков касательных. КT=26(см), NT=MT=26-x (см) по свойству отрезков касательных. 4) FT=4+(26-x)=30-x(см), KF=4+x(см) 5) По теореме Пифагора: 6) PK=15(см) ; KF=19(см), FT=15(см) 7) S=1/2*KF*FT=1/2*19*15=142,5(см²) 8) Центр описанной окружности- середина гипотенузы, радиус равен половине гипотенузы, R=13(см). С=2пR, C=26п(см) 2 4 4 P P х х 4 4 26-х 26-х

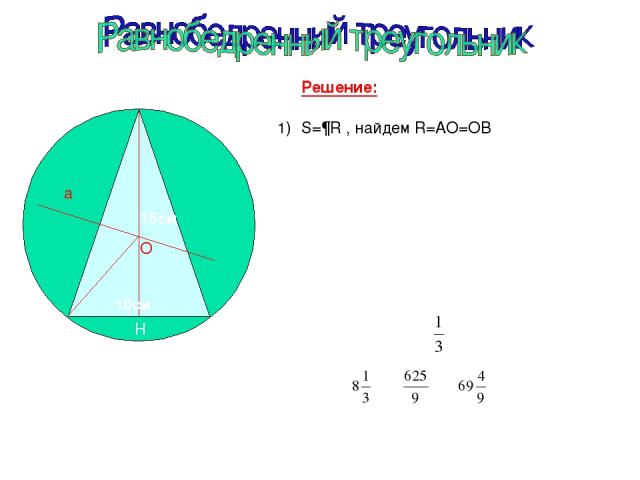
Задача №7. В равнобедренном треугольнике ABC c основанием АС=10 см, проведена высота BH=15(см). Найти площадь описанной около него окружности. О А С В Построение чертежа: 1) Треугольник АВС (АВ=ВС) 2) Точка О- центр описанной окружности, является пересечением серединных перпендикуляров а и BH (BH-медиана и высота по свойству равнобедренного треугольника). а Н 3) BO=AO=R- радиусы окружности

О А С В О А С В Решение: а H 10см 15см S=¶R , найдем R=AO=OB BH=15 (см), OH=15-R (см) 2) ∆АOH-прямоугольный (угол AHO=90º) AH=10:2=5(см) по определению медианы BH. 3) По теореме Пифагора: AO =AH +HO 5 +(15-R) =R , 25+(225-30R+R )=R 250-30R=0, R=8 (см) 4) S=¶( ) = ¶= ¶ (см)

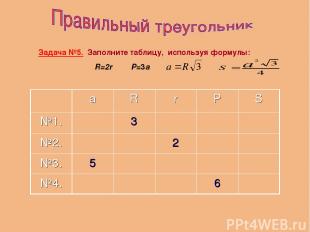
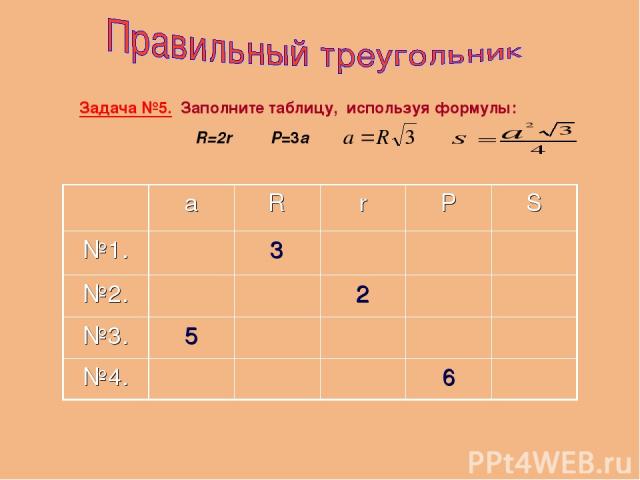
Задача №5. Заполните таблицу, используя формулы: R=2r P=3a а R r P S №1. 3 №2. 2 №3. 5 №4. 6

а R r P S №1. 3 1,5 №2. 4 2 №3. 5 15 №4. 2 6

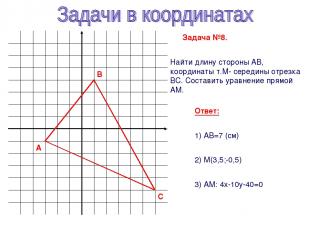
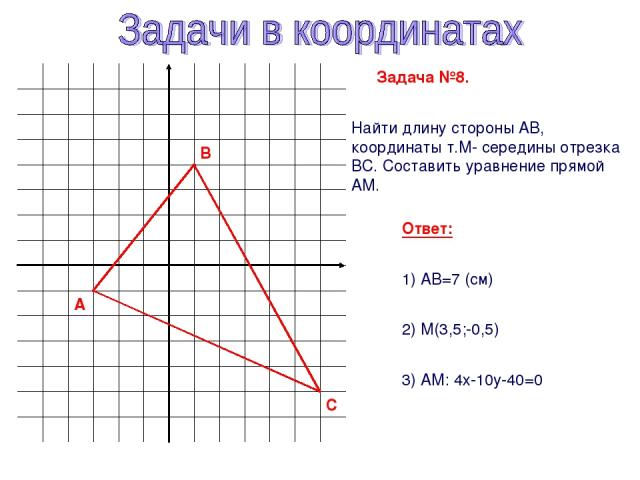
y x А В С Задача №8. Найти длину стороны АВ, координаты т.М- середины отрезка ВС. Составить уравнение прямой АМ. Ответ: 1) АВ=7 (см) 2) М(3,5;-0,5) 3) АМ: 4х-10y-40=0

Повторить тему: «Подобие треугольников» Глава №8. стр.133-157. 2) Около тупоугольного треугольника описана окружность с радиусом 25 см. Расстояние от ее центра до основания треугольника равно 7 см. Найти расстояние от центра окружности до боковой стороны треугольника 3) В треугольнике АВС угол С равен 60º, АВ=8см. На основании АВ как на диаметре построена окружность, пересекающая стороны АВ и ВС в точках К и М соответствкнно. Найти КМ.