Презентация на тему: Виды движения

Основные виды движений Обобщающий урок по теме «ДВИЖЕНИЯ». Учитель: ГОНЧАРОВА АННА ИВАНОВНА Шк. №569 Невского р-на. 900igr.net

Содержание. 1.Определения: 1.1.Преобразование фигур. 2.2.Отображение плоскости на себя. 1.3.Движение фигуры. 1.4.Движение плоскости. 1.5.Гомотетия. 2.Задача на усвоение понятия движения. 3.Основные виды движений. 4.Осевая симметрия. 4.1.Построение симметричных точек. 4.2.Осевая симметрия - движение. 4.3.Симметрия в системе координат. 4.4.Задача на построение 4.5.Симметрия фигур. (продолжение…)

Содержание. 5.Центральная симметрия. 5.1.Построение симметричных точек и отрезков. 5.2.Центральная симметрия в системе координат. 5.3.Задача на построение. 5.4.Центрально-симметричные фигуры. 6.Поворот. 6.1.Поворот – движение. 6.2.Центр. симметрия – поворот плоскости на 1800. 6.3.Задача на построение. 7.Параллельный перенос. 7.1.Параллельный перенос- движение. 7.2.Параллельный перенос на плоскости в системе координат. 7.3.Задача на построение. 8.Раздаточный материал. 9.Пояснительная записка. (WORD).

Определения. Преобразование фигур. Движение фигур. Отображение плоскости на себя. Движение плоскости.

Фигура F' получена преобразованием фигуры F. Фигура F' является образом фигуры F при данном преобразовании. Фигуру F называют прообразом фигуры F'. Преобразование фигур. Каждой точке фигуры F сопоставлена единственная точка плоскости. Пример:

Пример преобразования фигуры: Сжатие к оси X: Если каждой точке М(x,y) ставим в соответствие М'(x',y') и x'=x, y'= ky, где k>0- постоянное число. (если k>1- растяжение k

Отображение плоскости на себя. Если 1) каждой точке плоскости сопоставляется какая-то одна точка этой же плоскости, причем 2) каждая точка плоскости оказывается сопоставленной какой-то точке , тогда говорят, что дано отображение плоскости на себя. Примеры: Контрпример: Осевая и центральная симметрия плоскости.

Пример соответствия между точками плоскости, не являющимся отображением плоскости на себя: Ортогональная проекция каждой точки плоскости на данную прямую: Нарушено условие 2): Любая точка плоскости, не лежащая на данной прямой, не будет сопоставлена никакой точке плоскости ( плоскость отображается не на себя, а на прямую). x

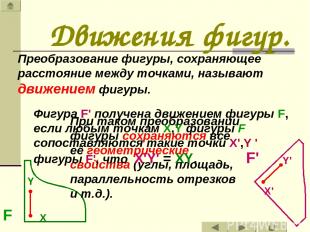
Движения фигур. Преобразование фигуры, сохраняющее расстояние между точками, называют движением фигуры. При таком преобразовании фигуры сохраняются все её геометрические свойства (углы, площадь, параллельность отрезков и т.д.). Фигура F' получена движением фигуры F, если любым точкам X,Y фигуры F сопоставляются такие точки X',Y ' фигуры F', что X'Y' = XY.

Движение плоскости- отображение плоскости на себя, которое сохраняет расстояния между точками. Отрезок движением переводится в отрезок. Луч при движении переходит в луч, прямая – в прямую. Треугольник движением переводится в треугольник. Контрпример:

Гомотетия . Гомотетией с центром O и коэффициентом k  ≠  0 называется преобразование, при котором каждой  точке X ставится в соответствие точка X' так, что Например, центральное подобие (гомотетия) с коэффициентом 2 : при k=2 расстояния между точками увеличиваются вдвое.

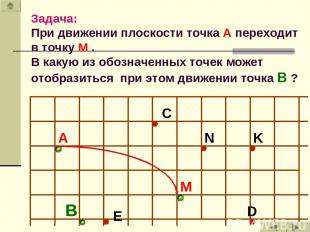
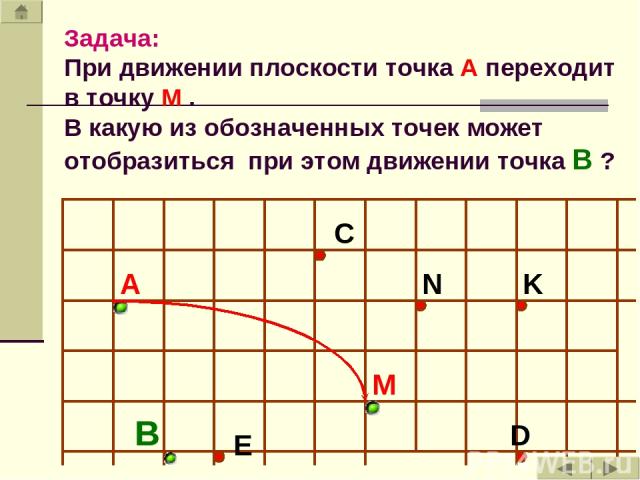
Задача: При движении плоскости точка А переходит в точку М . В какую из обозначенных точек может отобразиться при этом движении точка В ? B

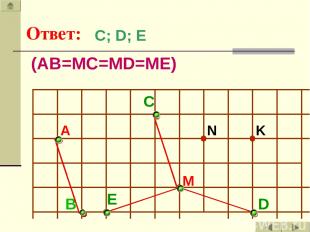
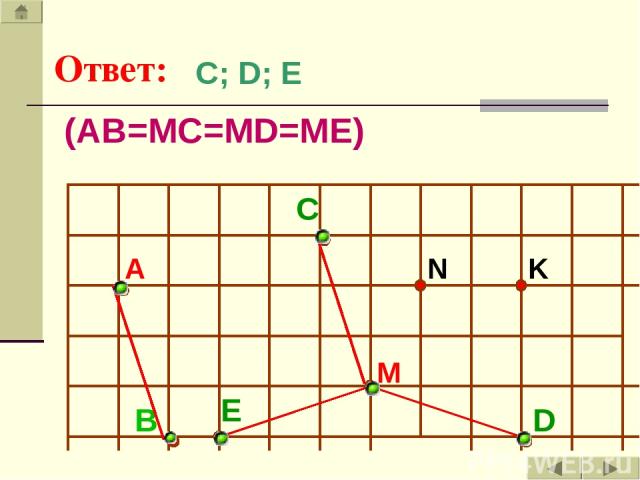
Ответ: А C N K M B E D С; D; E (AB=MC=MD=ME)

Основные виды движений: Осевая и центральная симметрии Поворот Параллельный перенос

Точки X и X' называются симметричными относительно прямой a, и каждая из них – симметричной другой, если a является серединным перпендикуляром отрезка XX' .  Осевая симметрия.

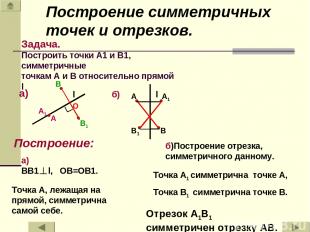
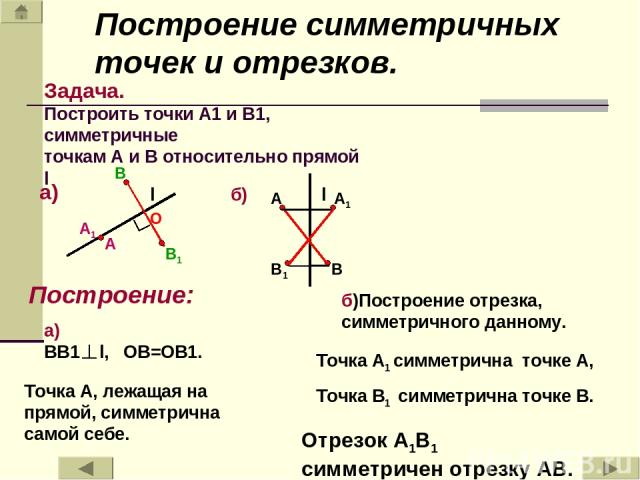
l а) A1 l б) В1 Задача. Построить точки А1 и B1, симметричные точкам А и В относительно прямой l Построение: а) ВВ1 l, ОВ=ОВ1. Точка А, лежащая на прямой, симметрична самой себе. б)Построение отрезка, симметричного данному. Точка А1 симметрична точке А, Точка В1 симметрична точке В. Отрезок А1В1 симметричен отрезку АВ. Построение симметричных точек и отрезков.

Осевой симметрией с осью a называется такое преобразование фигуры ,при котором каждой точке данной фигуры сопоставляется точка, симметричная ей относительно прямой a .

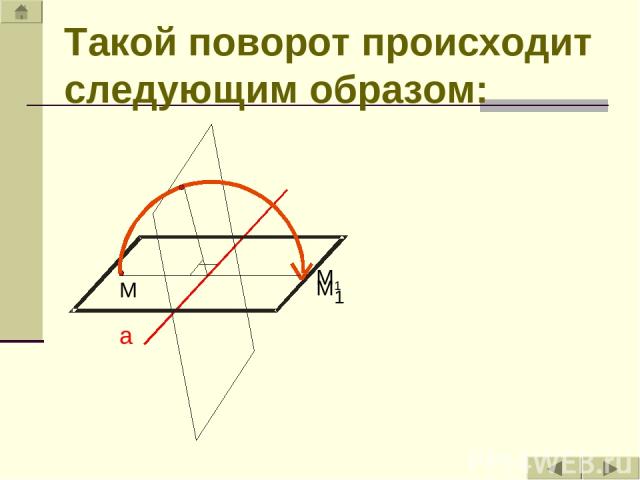
Осевая симметрия является движением . Почему отображение, сохраняющее расстояния, называется движением? Это можно пояснить на примере осевой симметрии. Её можно представить как поворот плоскости в пространстве на 1800 вокруг оси а.

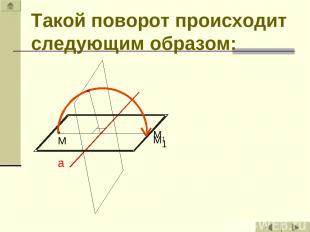
а М1 Такой поворот происходит следующим образом:

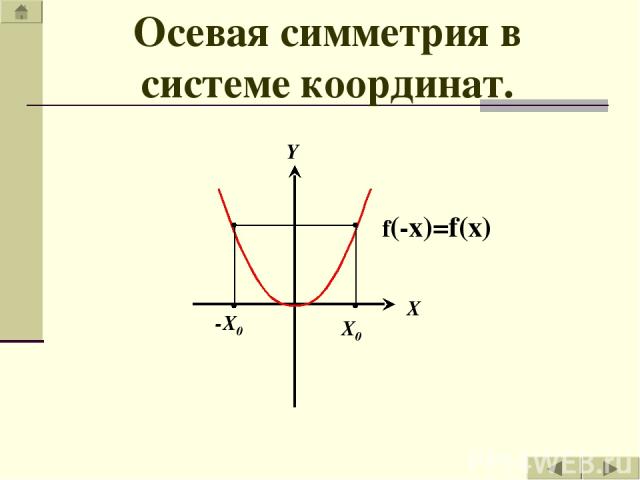
Осевая симметрия в системе координат.

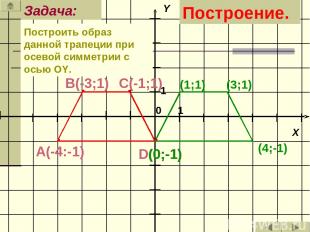
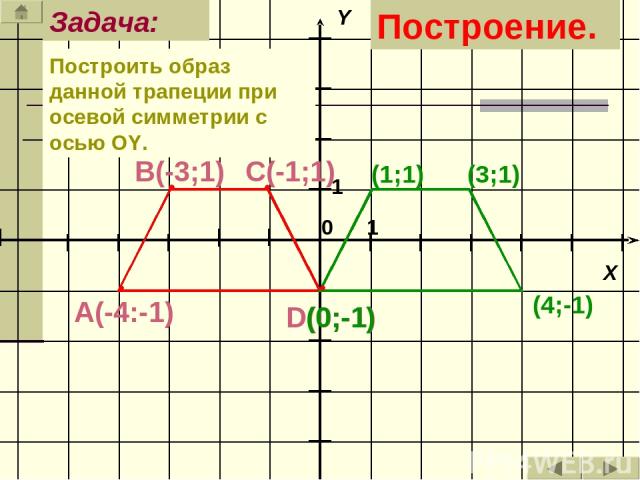
Построить образ данной трапеции при осевой симметрии с осью ОY. Задача: (3;1) (1;1) (0;-1) (4;-1) Построение.

Симметрия фигуры. Фигура называется симметричной относительно прямой a, если для каждой точки фигуры симметричная ей точка относительно прямой а также принадлежит этой фигуре. Фигура F симметрична относительно прямой а. Прямая а является ее осью симметрии .

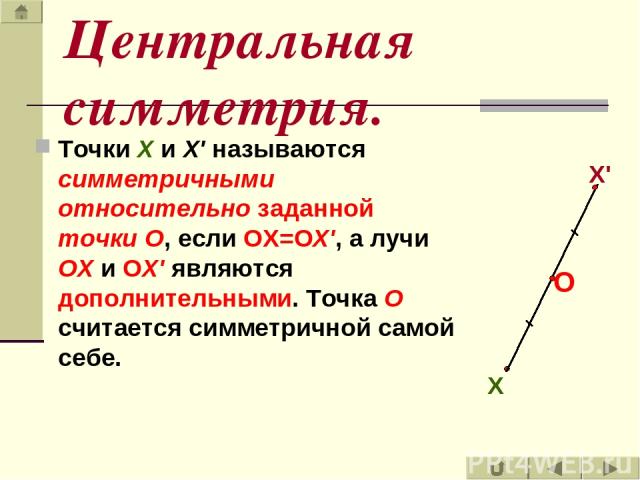
Точки X и Х' называются симметричными относительно заданной точки O, если ОХ=ОХ', а лучи OX и ОХ' являются дополнительными. Точка O считается симметричной самой себе. Центральная симметрия.

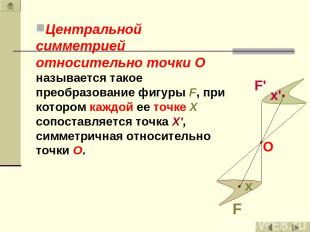
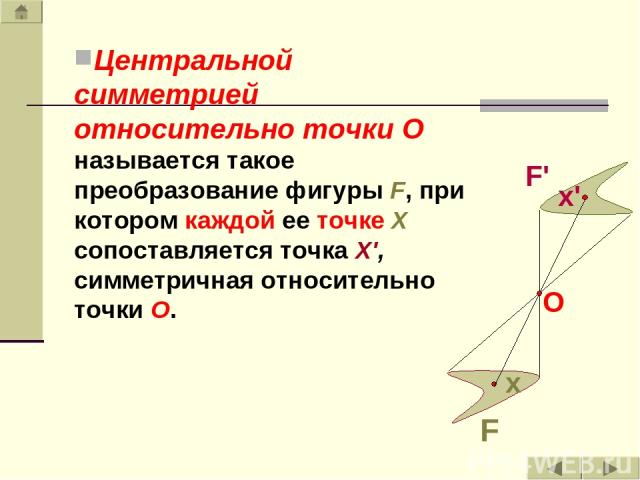
Центральной симметрией относительно точки O называется такое преобразование фигуры F, при котором каждой ее точке X сопоставляется точка Х', симметричная относительно точки O.

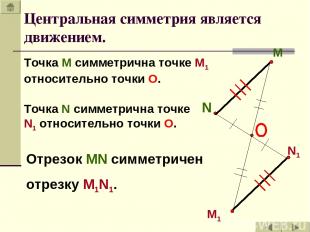
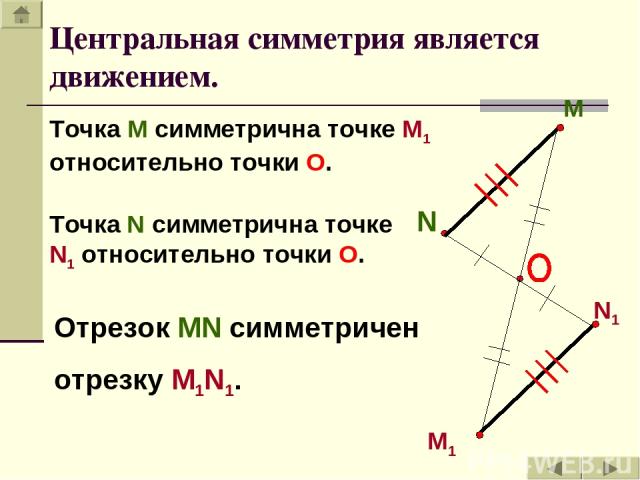
M N N1 M1 Точка М симметрична точке М1 относительно точки О. Точка N симметрична точке N1 относительно точки О. Отрезок MN симметричен отрезку M1N1. Центральная симметрия является движением.

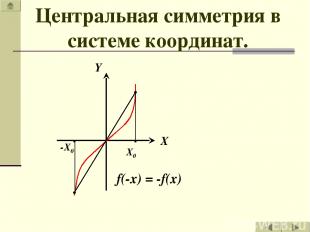
Центральная симметрия в системе координат.

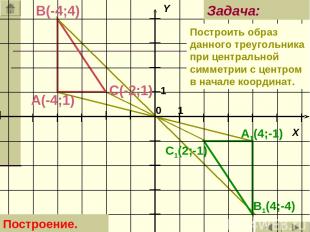
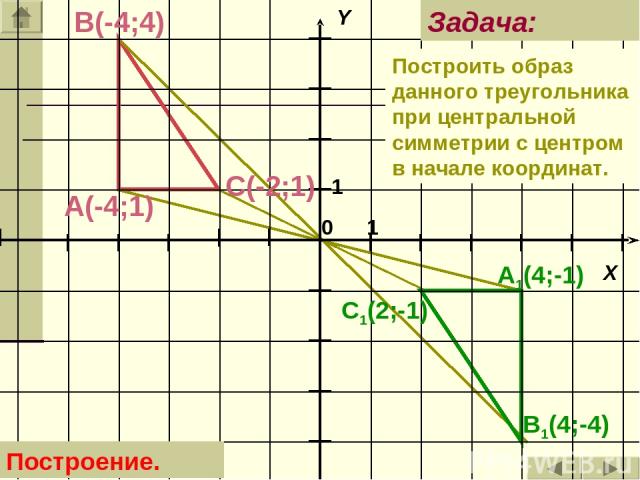
B1(4;-4) С(-2;1) A1(4;-1) C1(2;-1) А(-4;1) В(-4;4) Задача: Построение. Построить образ данного треугольника при центральной симметрии с центром в начале координат.

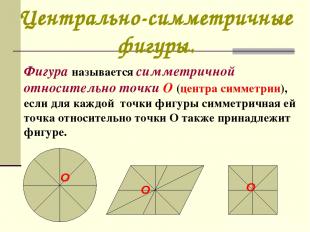
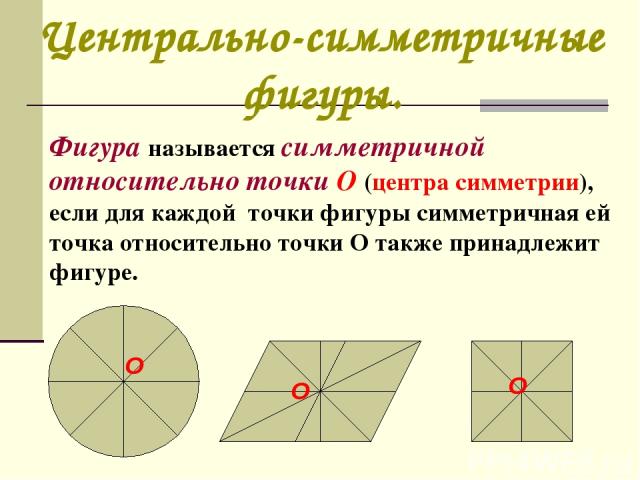
Центрально-симметричные фигуры. Фигура называется симметричной относительно точки О (центра симметрии), если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит фигуре.

ПОВОРОТ

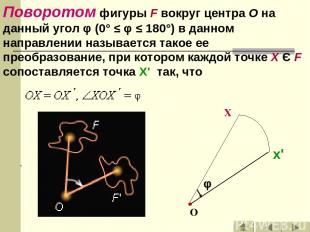
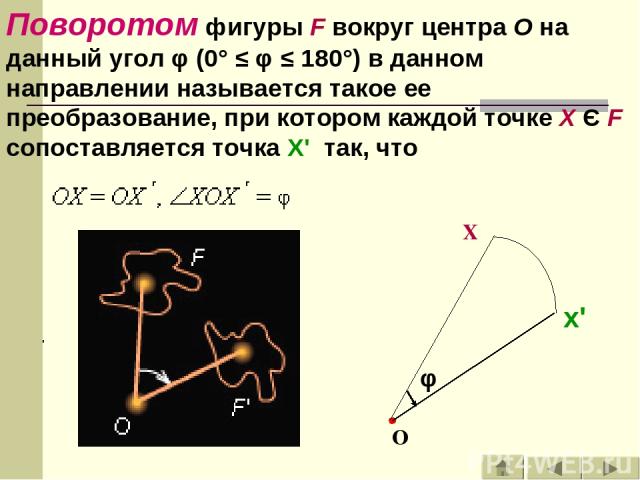
Поворотом фигуры F вокруг центра O на данный угол φ (0° ≤ φ ≤ 180°) в данном направлении называется такое ее преобразование, при котором каждой точке X Є F сопоставляется точка X' так, что x'

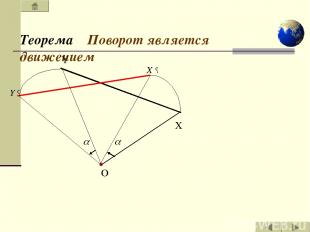
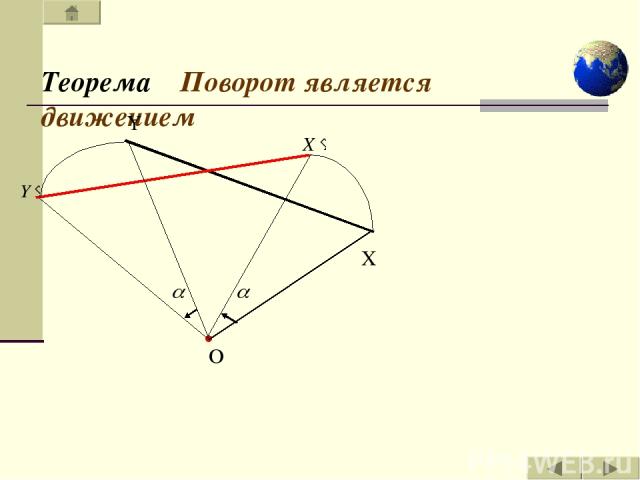
Теорема Поворот является движением О Y X

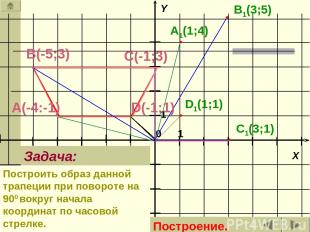
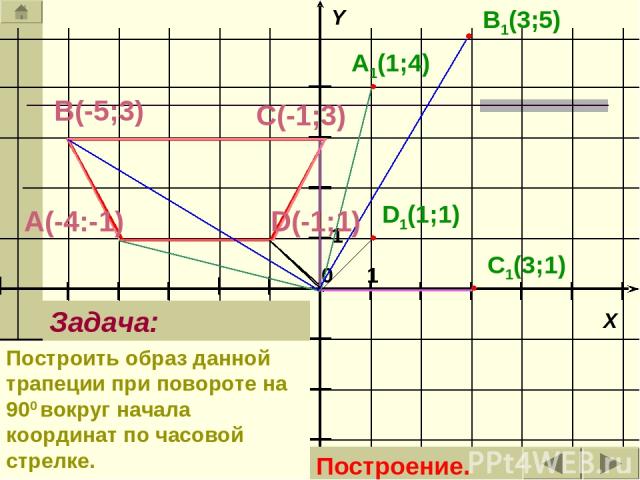
А(-4:-1) В(-5;3) D(-1;1) С(-1;3) A1(1;4) B1(3;5) C1(3;1) D1(1;1) Задача: Построить образ данной трапеции при повороте на 900 вокруг начала координат по часовой стрелке. Построение.

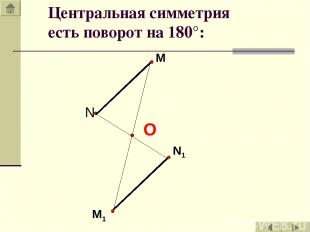
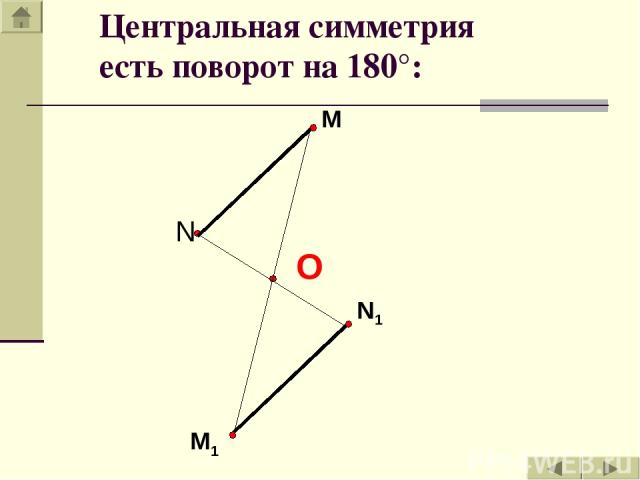
M N N1 M1 Центральная симметрия есть поворот на 180°: О

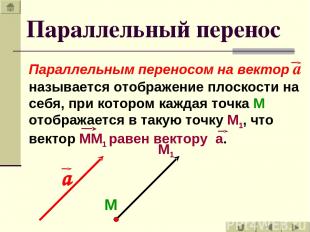
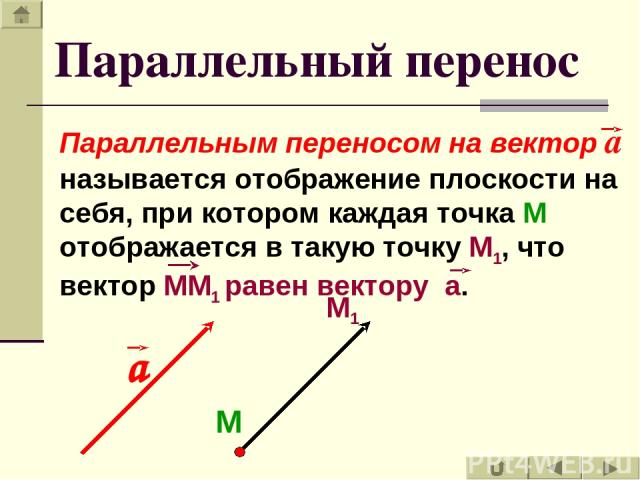
Параллельный перенос Параллельным переносом на вектор а называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что вектор ММ1 равен вектору а. М М1

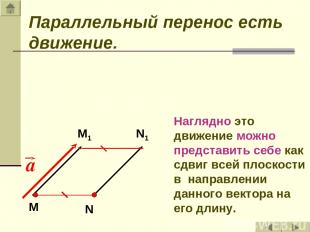
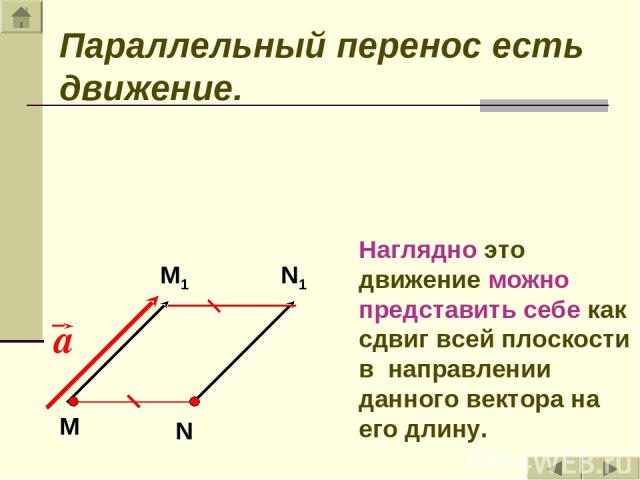
Параллельный перенос есть движение. Наглядно это движение можно представить себе как сдвиг всей плоскости в направлении данного вектора на его длину.

Параллельный перенос на плоскости в системе координат. Введем на плоскости систему координат O, X, Y. Преобразование фигуры F, при котором произвольная ее точка M (x; y) переходит в точку M' (x+a;y+b) , где a и b – одни и те же для всех точек (x; y), называется параллельным переносом.

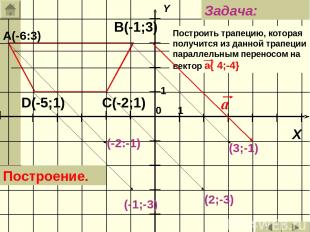
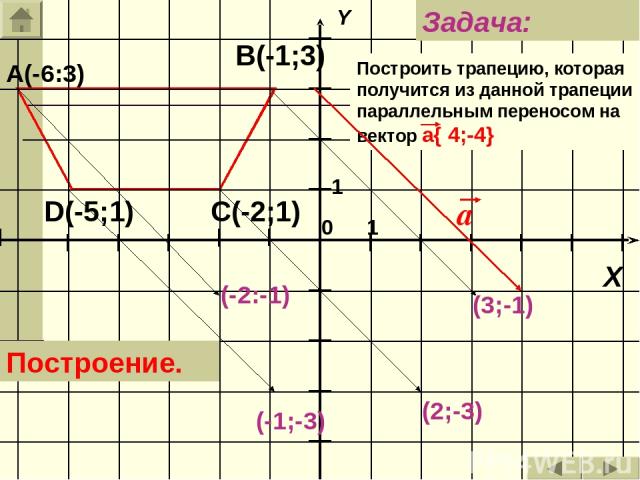
А(-6:3) В(-1;3) С(-2;1) D(-5;1) Построить трапецию, которая получится из данной трапеции параллельным переносом на вектор а{ 4;-4} Задача: Построение. (-2:-1) (3;-1) (2;-3) (-1;-3)

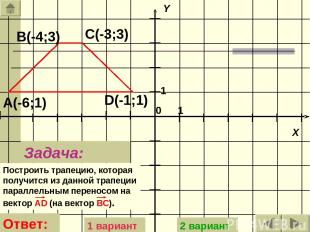
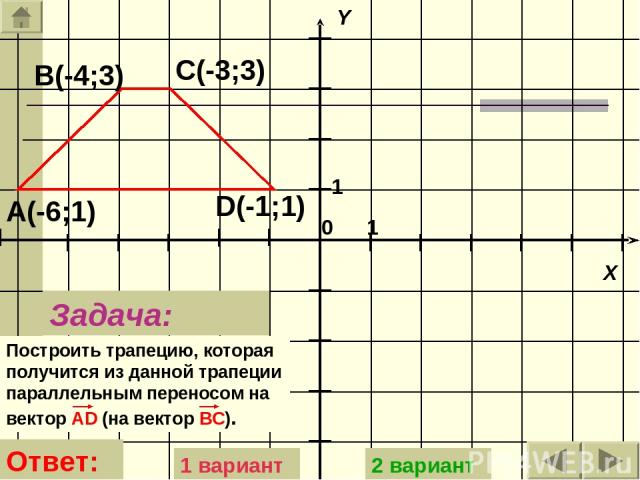
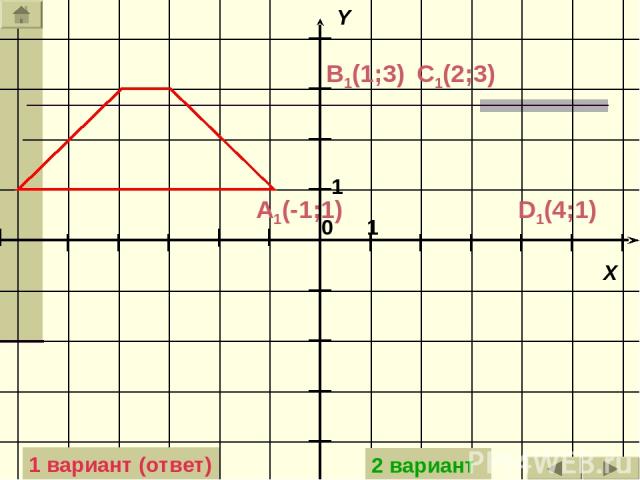
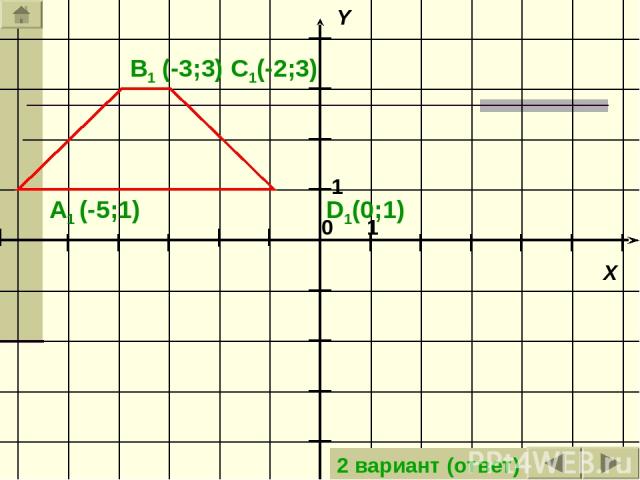
Задача: Построить трапецию, которая получится из данной трапеции параллельным переносом на вектор АD (на вектор BC). А(-6;1) В(-4;3) С(-3;3) D(-1;1) Ответ: 1 вариант 2 вариант

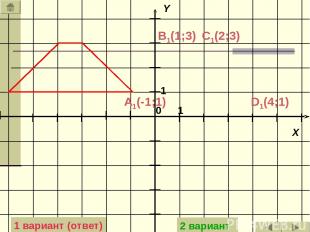
C1(2;3) D1(4;1) B1(1;3) A1(-1;1) 1 вариант (ответ) 2 вариант

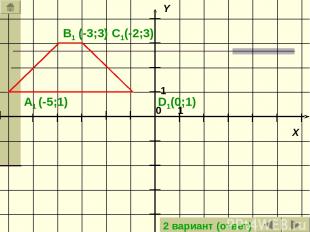
A1 (-5;1) B1 (-3;3) C1(-2;3) D1(0;1) 2 вариант (ответ)

Урок окончен. Спасибо за внимание.

Раздаточный материал.

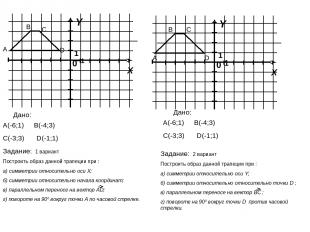
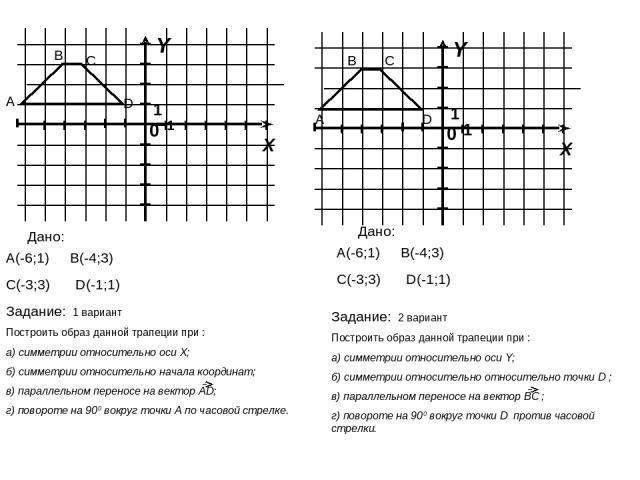
А Задание: 1 вариант Построить образ данной трапеции при : а) симметрии относительно оси X; б) симметрии относительно начала координат; в) параллельном переносе на вектор AD; г) повороте на 900 вокруг точки А по часовой стрелке. D(-1;1) А(-6;1) С(-3;3) В(-4;3) В С D Дано: В С D D(-1;1) А(-6;1) С(-3;3) В(-4;3) Дано: Задание: 2 вариант Построить образ данной трапеции при : а) симметрии относительно оси Y; б) симметрии относительно относительно точки D ; в) параллельном переносе на вектор BC ; г) повороте на 900 вокруг точки D против часовой стрелки. А