Презентация на тему: Виды движения тел

ДВИЖЕНИЕ Движением называется преобразование пространства, сохраняющее расстояния между точками, т. е., если точки A и B переходят соответственно в точки A’ и B’, то AB = A’B’. Теорема 1. Центральная симметрия является движением. Доказательство. Пусть точки A', B' получены центральной симметрией относительно точки О точек А, В. Тогда треугольники ОАВ и ОА'B' равны по первому признаку равенства треугольников (по двум сторонам и углу между ними) и, значит, АВ = A'B'. Таким образом, центральная симметрия сохраняет расстояния и, следовательно, является движением. 900igr.net

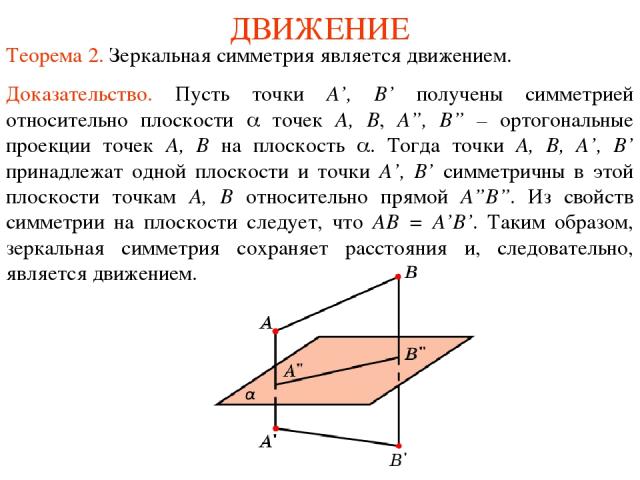
ДВИЖЕНИЕ Теорема 2. Зеркальная симметрия является движением. Доказательство. Пусть точки A’, B’ получены симметрией относительно плоскости точек A, B, A”, B” – ортогональные проекции точек A, B на плоскость . Тогда точки A, B, A’, B’ принадлежат одной плоскости и точки A’, B’ симметричны в этой плоскости точкам A, B относительно прямой A”B”. Из свойств симметрии на плоскости следует, что AB = A’B’. Таким образом, зеркальная симметрия сохраняет расстояния и, следовательно, является движением.

Упражнение 1 Назовите движение, которое оставляет на месте только: а) одну точку; б) точки одной прямой; в) точки одной плоскости. Ответ: а) Центральная симметрия; б) осевая симметрия; в) зеркальная симметрия.

Упражнение 2 Существуют ли движения (если существуют, то какие), переводящие данную прямую в другую данную прямую: а) параллельную первой; б) пересекающую первую; в) скрещивающуюся с первой? Ответ: а) Центральная симметрия, зеркальная симметрия, параллельный перенос; б) осевая симметрия, поворот, зеркальная симметрия; в) осевая симметрия.

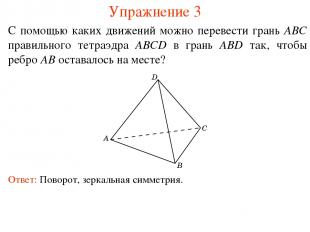
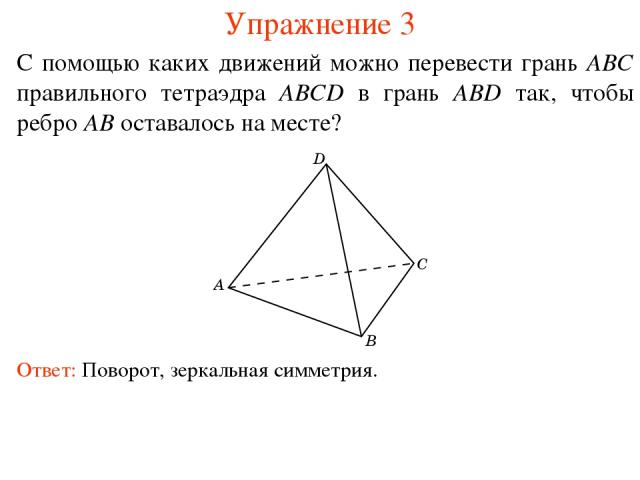
Упражнение 3 С помощью каких движений можно перевести грань ABC правильного тетраэдра ABCD в грань ABD так, чтобы ребро AB оставалось на месте? Ответ: Поворот, зеркальная симметрия.

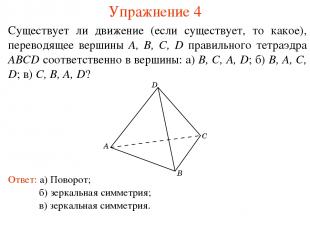
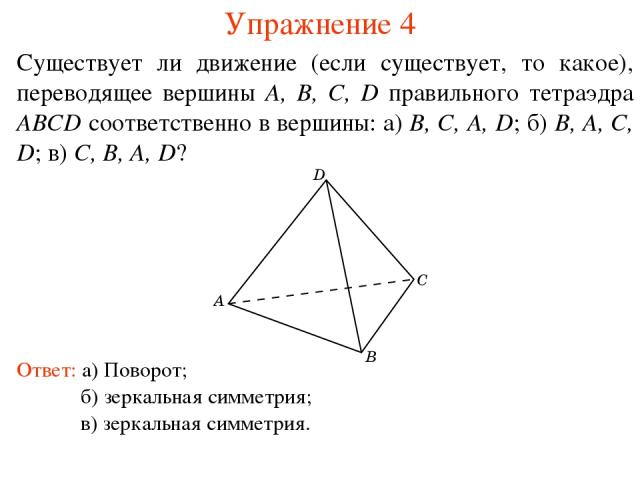
Упражнение 4 Существует ли движение (если существует, то какое), переводящее вершины A, B, C, D правильного тетраэдра ABCD соответственно в вершины: а) B, C, A, D; б) B, A, C, D; в) C, B, A, D? Ответ: а) Поворот; б) зеркальная симметрия; в) зеркальная симметрия.

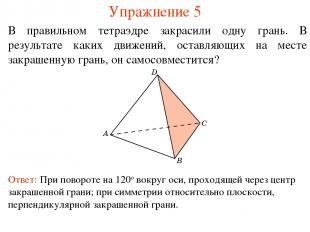
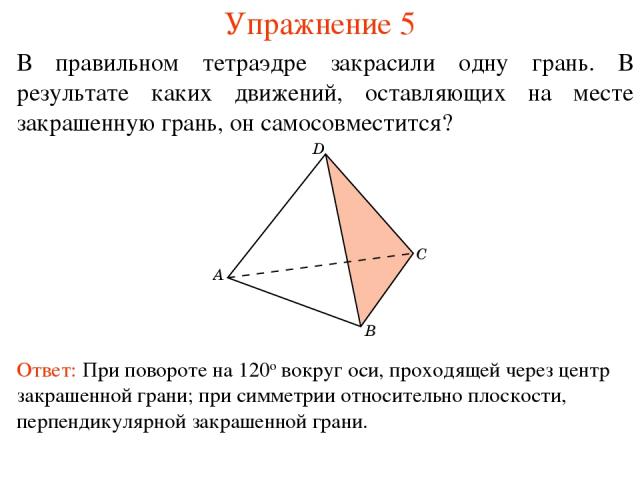
Упражнение 5 В правильном тетраэдре закрасили одну грань. В результате каких движений, оставляющих на месте закрашенную грань, он самосовместится? Ответ: При повороте на 120о вокруг оси, проходящей через центр закрашенной грани; при симметрии относительно плоскости, перпендикулярной закрашенной грани.

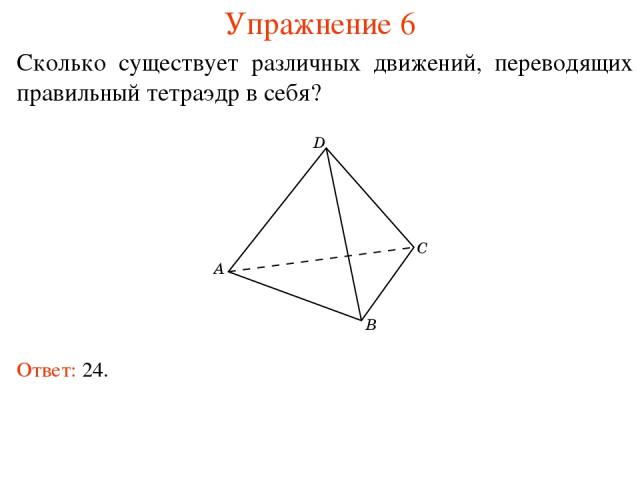
Упражнение 6 Сколько существует различных движений, переводящих правильный тетраэдр в себя? Ответ: 24.

Упражнение 7 Существует ли движение (если существует, то какое), переводящее вершины A, B, C, D куба A…D1 соответственно в вершины: а) A1, B1, C1, D1; б) A1, D1, C1, B1; в) A1, B1, D1, C1? Ответ: а) Да, параллельный перенос, зеркальная симметрия; б) да, осевая симметрия; в) нет.

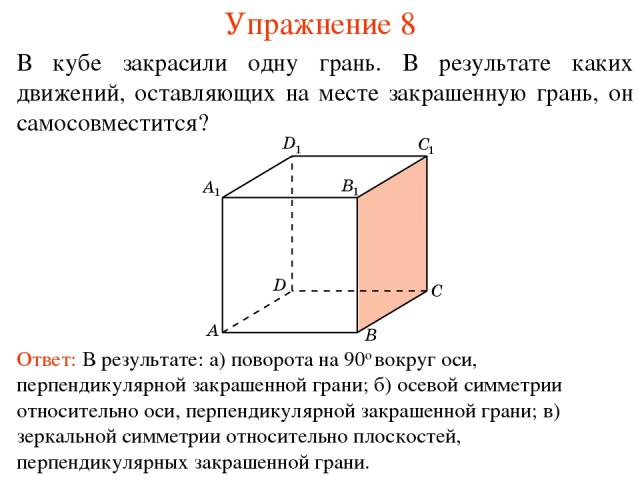
Упражнение 8 В кубе закрасили одну грань. В результате каких движений, оставляющих на месте закрашенную грань, он самосовместится? Ответ: В результате: а) поворота на 90о вокруг оси, перпендикулярной закрашенной грани; б) осевой симметрии относительно оси, перпендикулярной закрашенной грани; в) зеркальной симметрии относительно плоскостей, перпендикулярных закрашенной грани.

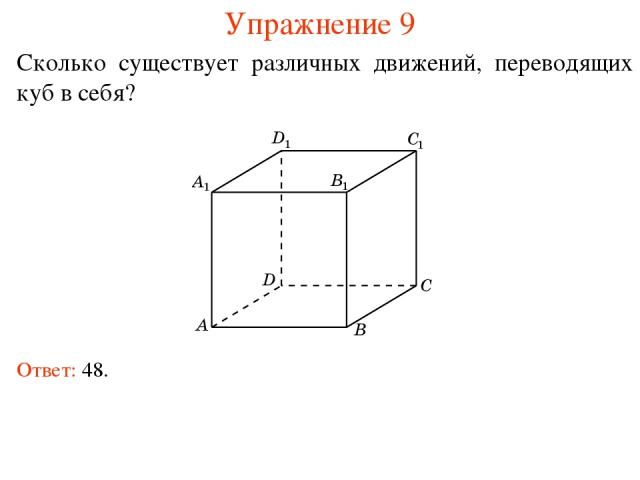
Упражнение 9 Сколько существует различных движений, переводящих куб в себя? Ответ: 48.

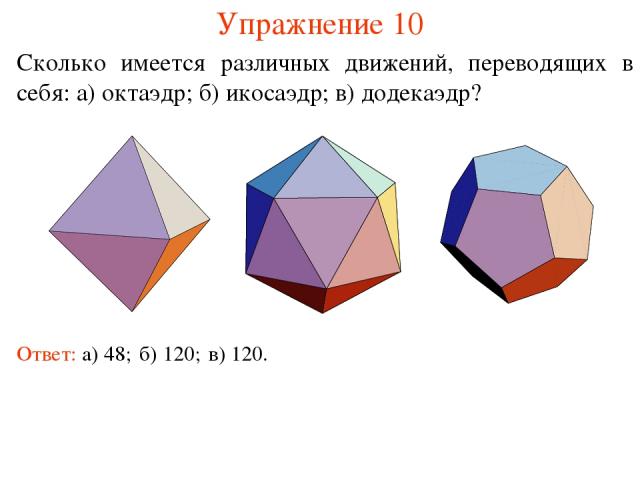
Упражнение 10 Сколько имеется различных движений, переводящих в себя: а) октаэдр; б) икосаэдр; в) додекаэдр? Ответ: а) 48; б) 120; в) 120.