Презентация на тему: Тригонометрические функции любого угла

Тригонометрические функции любого угла Определение синуса, косинуса, тангенса и котангенса.

Место урока в теме: первый урок по теме. Цели урока: -формирование новых понятий(угол поворота,sin, cos, tg, научить строить угол произвольной градусной меры и определять отношение угла к коорд. четверти; воспитание положительного отношения к знаниям; воспитание дисциплинированности; развитие умения делать обобщающие выводы, работать самостоятельно и в группах, работать в нужном темпе. Тип урока: урок изучения нового материала в классе КРО. Метод диалогического изложения материала с использованием ИТ. 1.Актуализация знаний.2.Формирование новых понятий, способов действий.3.Формирование умений и навыков. Виды деятельности на уроке( учитывая особенности класса):Работа классом, индивидуальная, групповая.
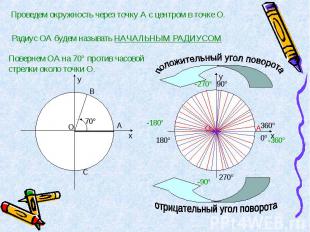
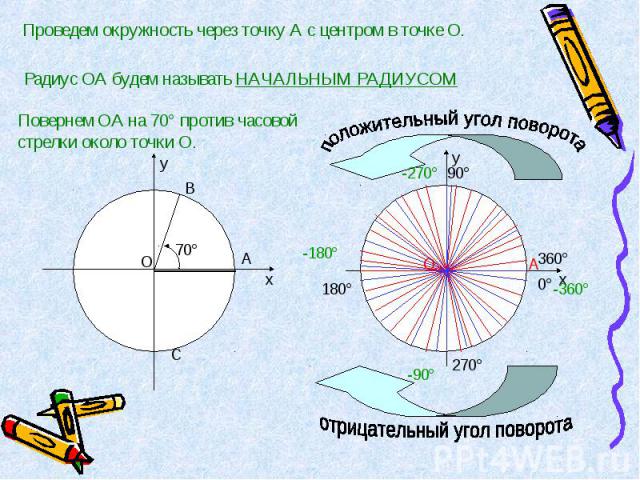
Проведем окружность через точку А с центром в точке О. Радиус ОА будем называть НАЧАЛЬНЫМ РАДИУСОМ Повернем ОА на 70° против часовой стрелки около точки О. положительный угол поворота отрицательный угол поворота

Таким образом, угол поворота может выражаться каким угодно числом от -∞ до +∞. Так, если начальный радиус ОА повернуть на 180°, а потом еще на 30°, то угол поворота будет равен 210°. Если начальный радиус ОА сделает полный оборот против часовой стрелки, то угол поворота будет равен 360° Существует бесконечно много углов поворота.

Задание 1: Изобразить угол поворота, равный 150°, -45°, -135°.

Так, если 0° ‹ α ‹ 90°, то α-угол I четверти если 90° ‹ α ‹ 180°, то α-угол II четверти; если 180° ‹ α ‹ 270°, то α-угол III четверти; если 270° ‹ α ‹ 360°, то α-угол IV четверти. Углы 0°, ±90°, ±180°, ±270°, ±360° не относятся ни к какой четверти. Угол в 430° является углом какой четверти ? т.к. 430°= 360°+70° и 0 °‹ 70°‹ 90°, то этот угол лежит в I четверти. Так, например, угол в 920° является углом III четверти, т.к. 920 °=360°▪ 2+200 °

Задание 2: Углом какой четверти является угол α, если:α=283°, 190°, -20°, -110°, 540 °, -720°.

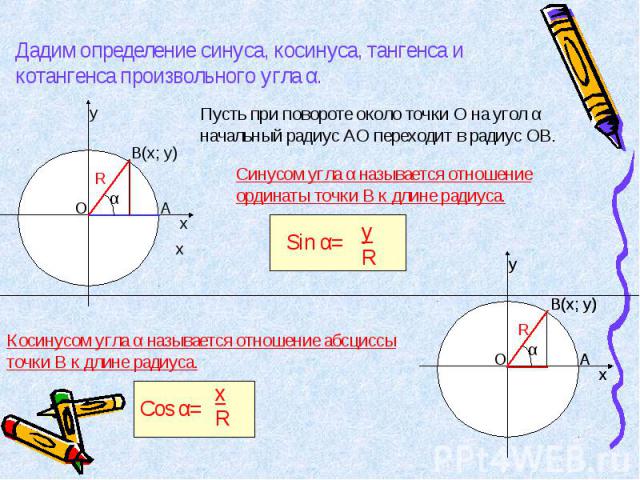
Дадим определение синуса, косинуса, тангенса и котангенса произвольного угла α. Пусть при повороте около точки О на угол α начальный радиус АО переходит в радиус ОВ. Синусом угла α называется отношение ординаты точки В к длине радиуса. Косинусом угла α называется отношение абсциссы точки В к длине радиуса.

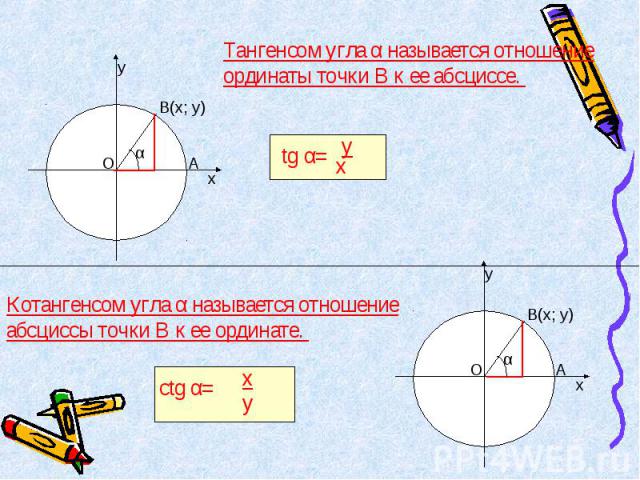
Тангенсом угла α называется отношение ординаты точки В к ее абсциссе. tg α= Котангенсом угла α называется отношение абсциссы точки В к ее ординате.

Выражения sinα, cosα определены при любом α, т.к. для любого угла поворота можно найти соответствующее значение дроби А при каком α выражения tgα и ctgα имеют смысл ? Каждому допустимому значению α соответствует единственное значение sinα, cosα, tgα и ctgα.Поэтому синус, косинус, тангенс и котангенс являются функциями угла α. Их называют тригонометрическими функциями.

Задание 3: Найти sin, cos, tg и ctg α, если α=50°, 90°,-100°.(используя определения)выполнить задание по группам, в одной группе R=4см, в другой-R=3см, по готовому чертежу. Вывод: отчего зависят тригонометрические функции?