Презентация на тему: Третий признак равенства треугольников

Третий признак равенства треугольников

Цели: изучить третий признак равенства треугольников, выработать навыки использования их при решении задач. систематизировать, расширить и углубить знания учащихся о треугольнике, закрепить навыки и умения при решении задач, используя определения и теоремы по данной теме.

Ход урока1.Организационный момент2.Повторение3.Изучение нового материала4.Закрепление из материала5.Домашнее задание

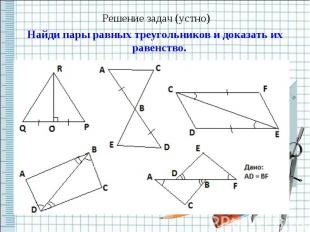
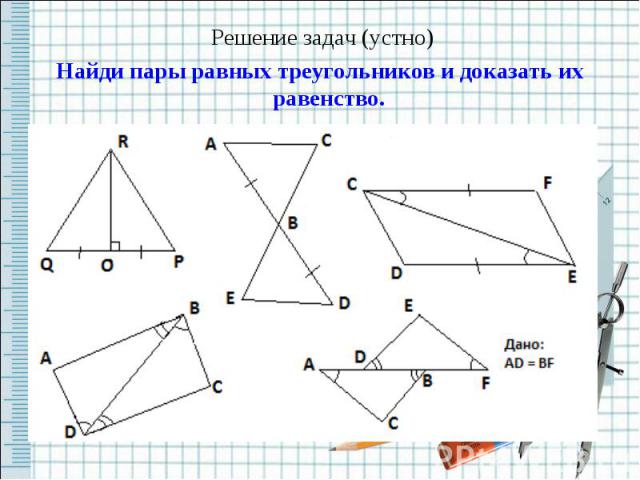
Решение задач (устно)Найди пары равных треугольников и доказать их равенство.

Теорема: Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника то такие треугольники равны Дано:∆ ABC, ∆ A1B1C1; AB = A1B1; BC = B1C1;AC = A1C1. Доказать: ∆ ABC = ∆ A1B1C1. Луч CC1 совпадает с одной из сторон угла B1C1A1.∆ B1C1C – равнобедренный с основанием CC1 так как B1C1 = BC = B1C (по условию)B1A1 –медиана, ∆ B1C1C (C1A1 = AC по условию) AC = A1C<C1B1A1 = <CBA (то есть медиана в равнобедренном треугольнике, является биссектрисой ) ∆ ABC = ∆ A1B1C1 (по двум сторонам и углу между ними) AB = A1B1; BC=B1C1 (по условию)<CAB = <C1B1A1 по доказанному. Ч.Т.Д.

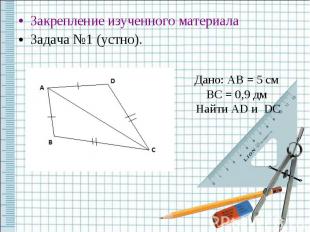
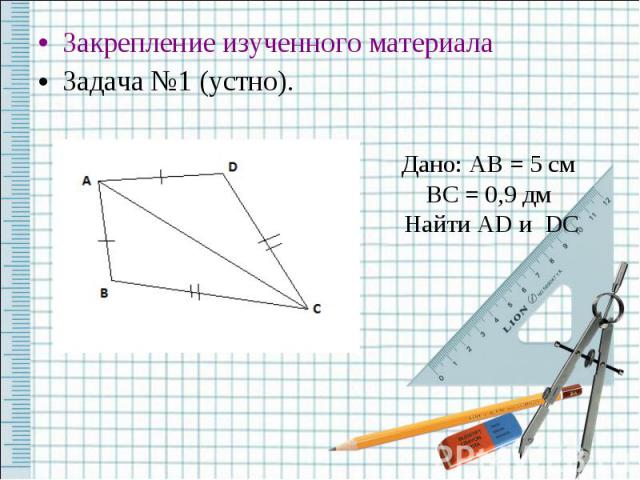
Закрепление изученного материалаЗадача №1 (устно). Дано: AB = 5 см BC = 0,9 дм Найти AD и DC

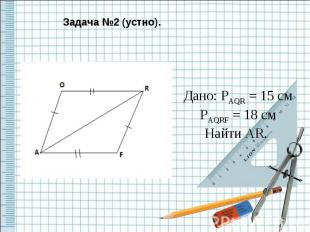
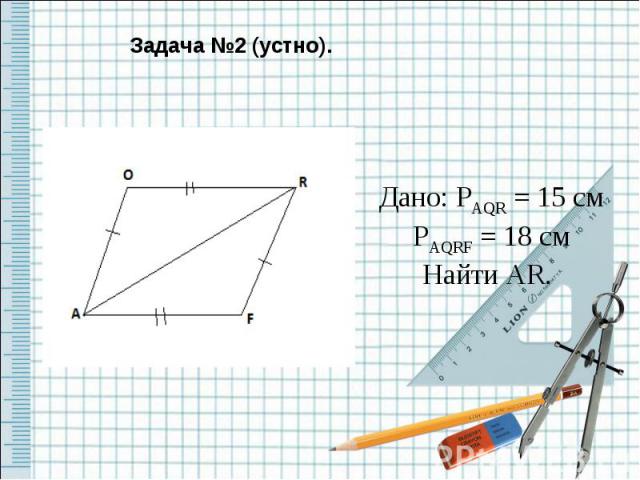
Задача №2 (устно). Дано: PAQR = 15 смPAQRF = 18 смНайти AR.

Стороны одного треугольника равны 30 см, 40 см и 0,5 м, а другого – 30 см, 40см и 5 дм. Равны ли эти треугольники?

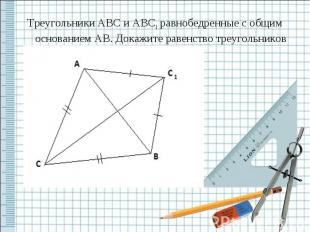
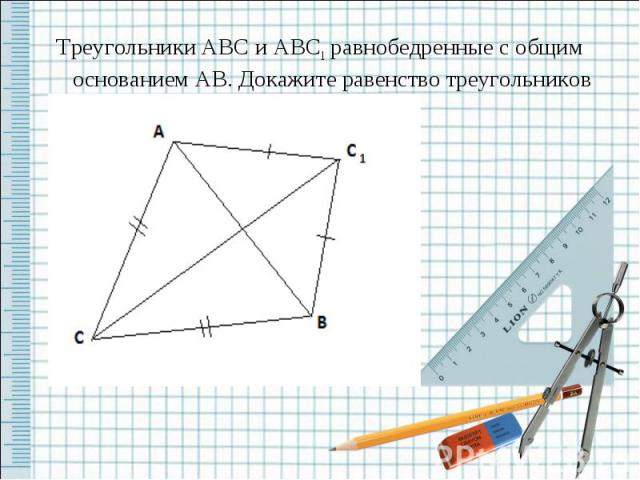
Треугольники ABC и ABC1 равнобедренные с общим основанием AB. Докажите равенство треугольников ACC1, и BCC1.

Решение: Рассмотрим ∆ACC1 и ∆ BCC1, AC = BC1 так как ∆ ABC1 – равнобедренный AC = CB так как треугольник ABC – равнобедренный Сторона CC1 – общая у ∆ ACC1 и ∆ BCC1 следственно ∆ ACC1 = ∆ BCC1 по трём сторонам. Ч.Т.Д Решить задачу № 138.

Домашнее задание п19, 20 вопр. 14-15 стр50. № 136, доказать 3 случай теоремы.Творческое задание: Придумайте задачу, для решения которой нужно знать признаки равенства треугольников. (Сделать чертёж и решить ее)