Презентация на тему: Решение задач на признаки равенства треугольников

Решение задач на признаки равенства треугольников

Признаки равенства треугольников Треугольник на евклидовой плоскости однозначно можно определить по следующим тройкам основных элементов:Равенство по двум сторонам и углу лежащему между ними; Равенство по стороне и двум прилежащим углам;Равенство по трём сторонам.

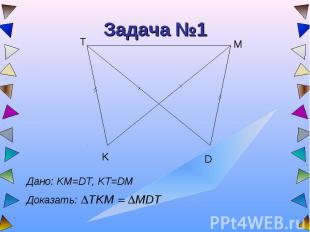
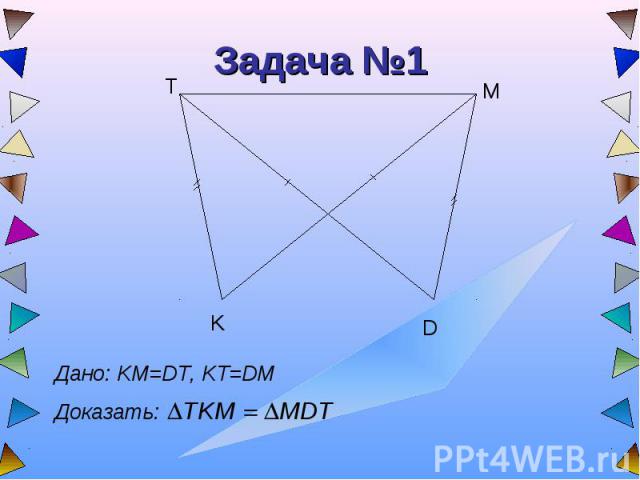
Задача №1 Дано: KM=DT, KT=DMДоказать:

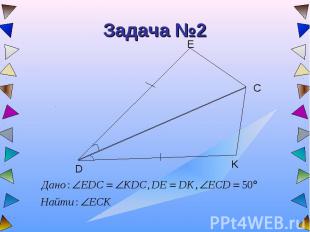
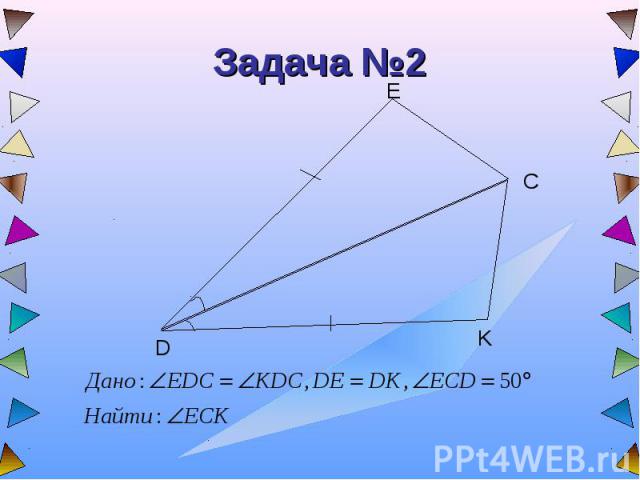
Задача №2

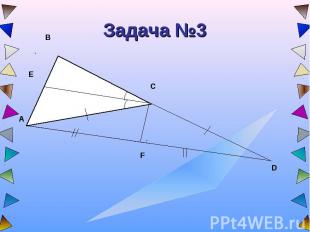
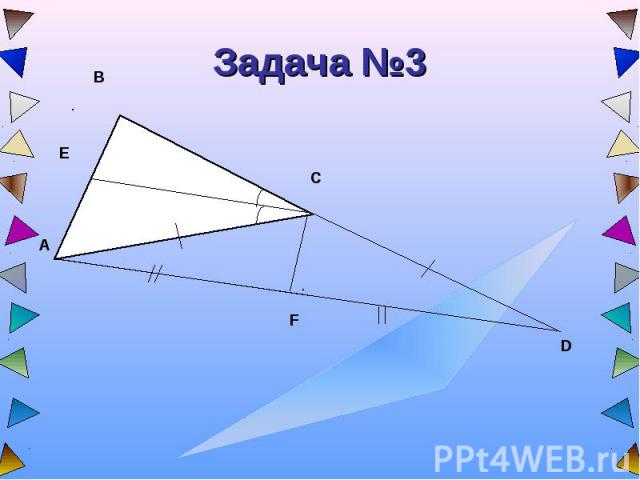
Задача №3

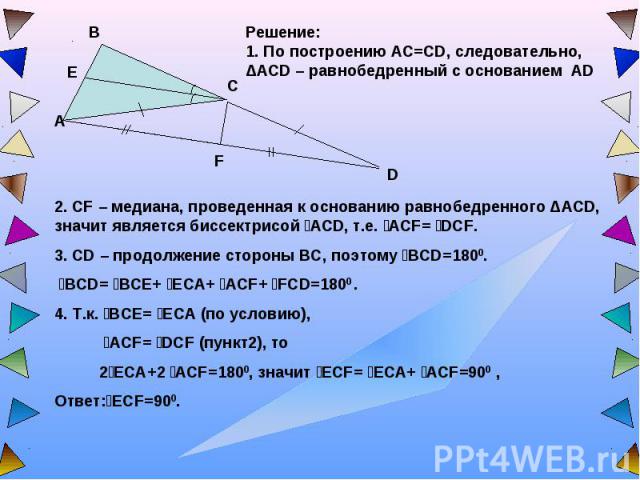
Решение:1. По построению AC=CD, следовательно, ΔACD – равнобедренный с основанием AD 2. CF – медиана, проведенная к основанию равнобедренного ΔACD, значит является биссектрисой ےACD, т.е. ےACF= ےDCF.3. CD – продолжение стороны ВС, поэтому ےВCD=1800. ےВCD= ےВCЕ+ ےЕCA+ ےACF+ ےFCD=1800 .4. Т.к. ےВCЕ= ےЕCA (по условию), ےACF= ےDCF (пункт2), то 2ےЕCA+2 ےACF=1800, значит ےЕCF= ےЕCA+ ےACF=900 ,Ответ:ےECF=900.

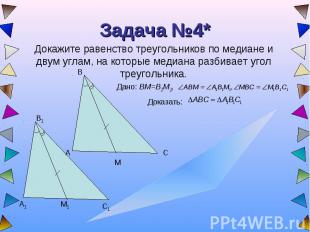
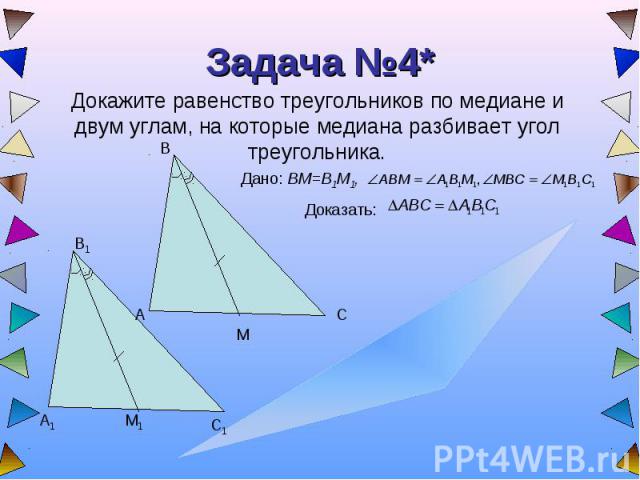
Задача №4* Докажите равенство треугольников по медиане и двум углам, на которые медиана разбивает угол треугольника.

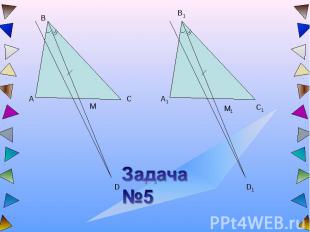
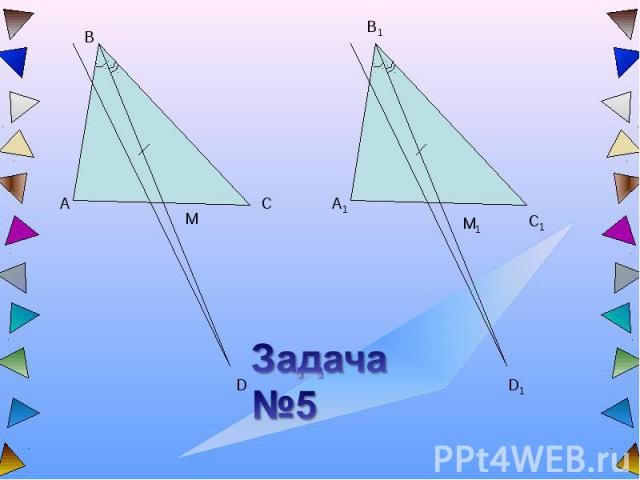
Задача №5

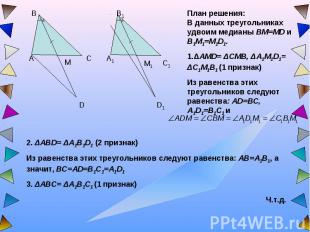
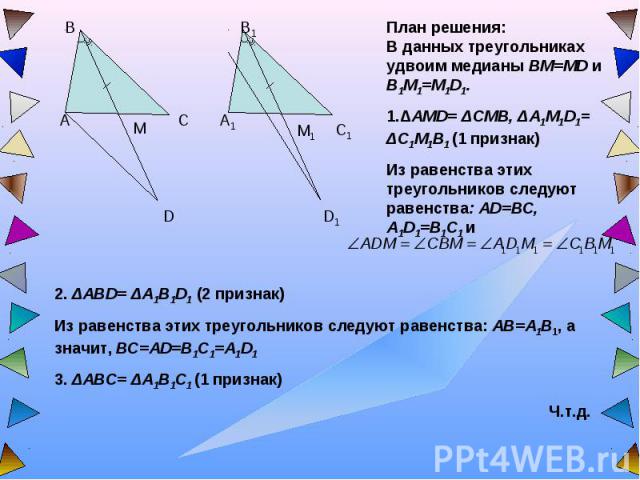
План решения:В данных треугольниках удвоим медианы BM=MD и B1M1=M1D1. 1.ΔAMD= ΔCMB, ΔA1M1D1= ΔC1M1B1 (1 признак)Из равенства этих треугольников следуют равенства: AD=BC, A1D1=B1C1 и 2. ΔABD= ΔA1B1D1 (2 признак)Из равенства этих треугольников следуют равенства: AB=A1B1, а значит, BC=AD=B1C1=A1D13. ΔABC= ΔA1B1C1 (1 признак)Ч.т.д.

Спасибо за внимание