Презентация на тему: Решение задач координатным методом

Решение задач на нахождение расстояний и углов в пространстве координатным методом Учитель математики МБОУ-СОШ №7 г.Клинцы Брянской области Коваленко С.Ф. 900igr.net

Математический диктант Записать в координатах : Условие коллинеарности двух векторов. Условие перпендикулярности двух векторов. Формулу для нахождения косинуса угла между векторами. Формулу для нахождения длины вектора. Уравнение плоскости. Ответы для самопроверки математического диктанта

Алгоритм решения задач Ввести прямоугольную систему координат - на плоскости основания многогранника; - в пространстве. Найти координаты точек, о которых идет речь в условии задачи. Найти координаты - направляющих векторов прямых; - векторов, перпендикулярных плоскостям (нормалей). Воспользоваться соответствующей формулой для нахождения - расстояний в пространстве; - углов в пространстве.

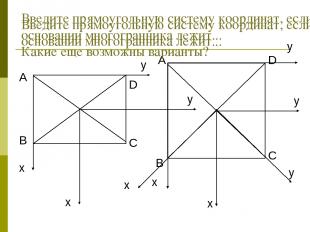
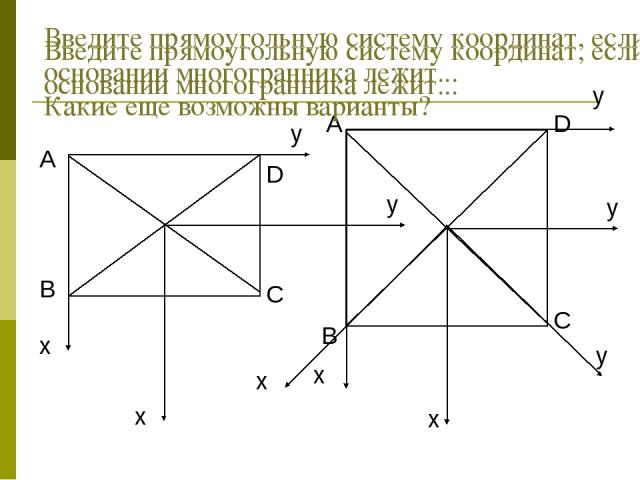
Введите прямоугольную систему координат, если в основании многогранника лежит... Введите прямоугольную систему координат, если в основании многогранника лежит... Какие еще возможны варианты?

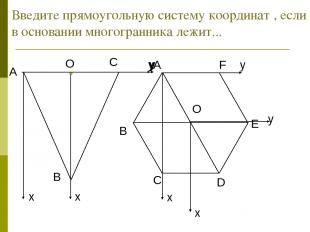
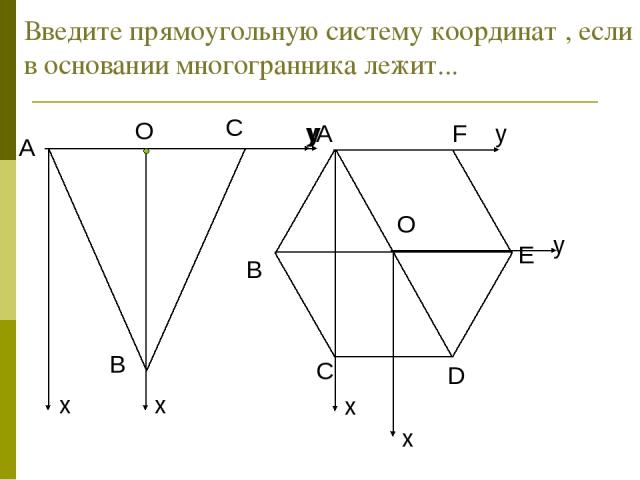
Введите прямоугольную систему координат , если в основании многогранника лежит...

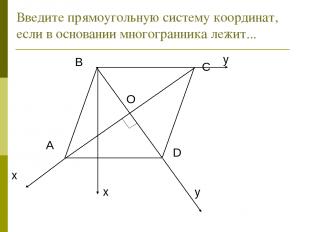
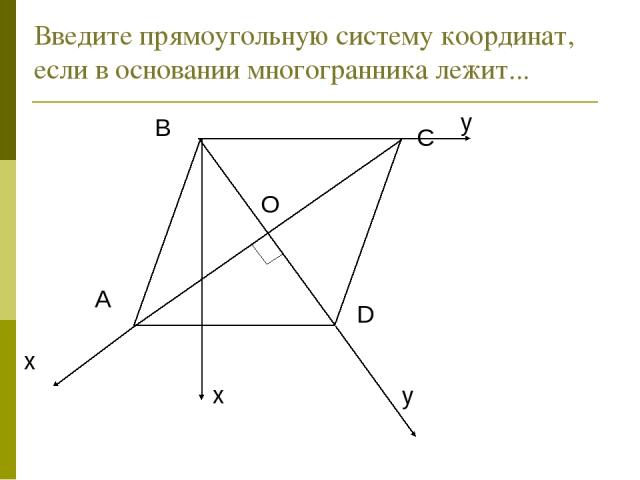
Введите прямоугольную систему координат, если в основании многогранника лежит... A B C D O

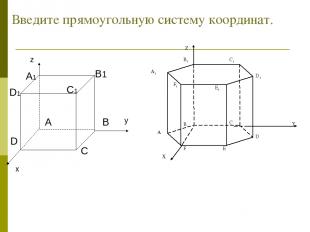
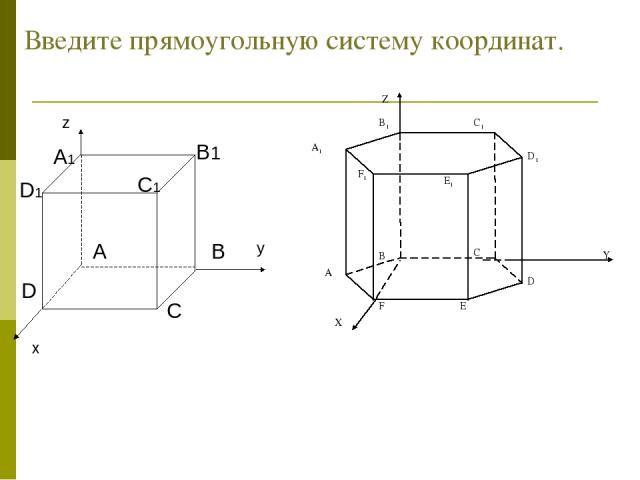
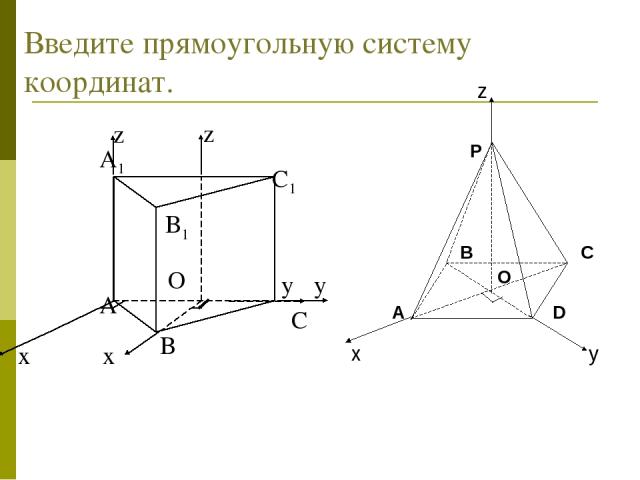
Введите прямоугольную систему координат.

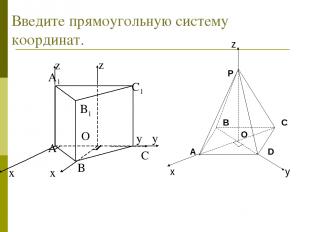
Введите прямоугольную систему координат.

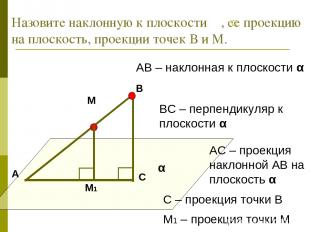
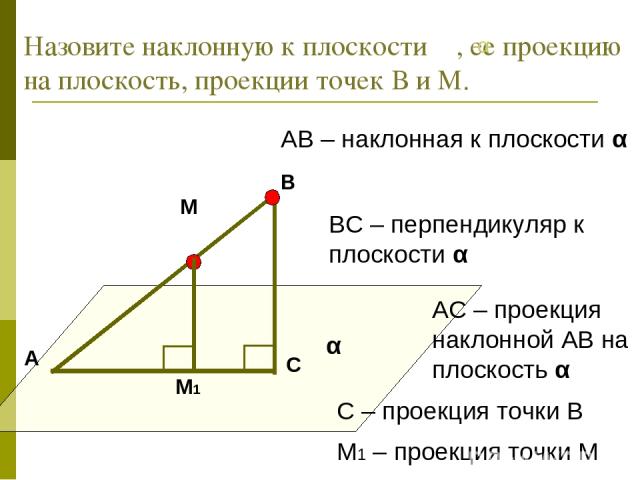
АС – проекция наклонной АВ на плоскость α АВ – наклонная к плоскости α ВС – перпендикуляр к плоскости α С – проекция точки В α М М1 Назовите наклонную к плоскости , ее проекцию на плоскость, проекции точек В и М. α М1 – проекция точки М

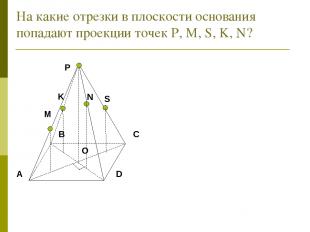
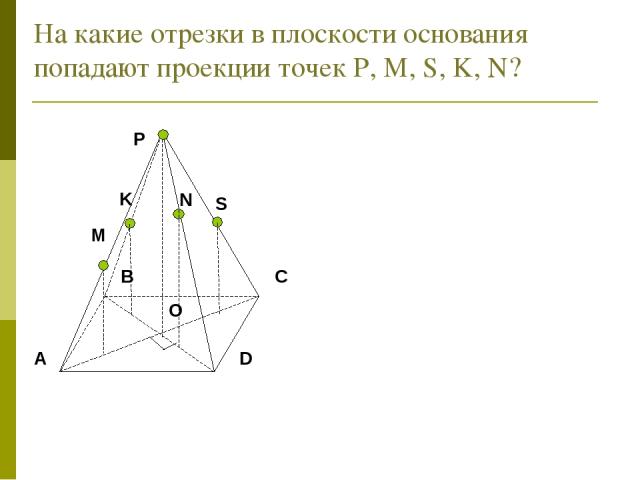
На какие отрезки в плоскости основания попадают проекции точек Р, М, S, K, N? N K S

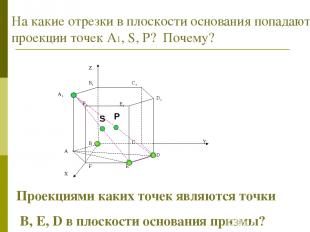
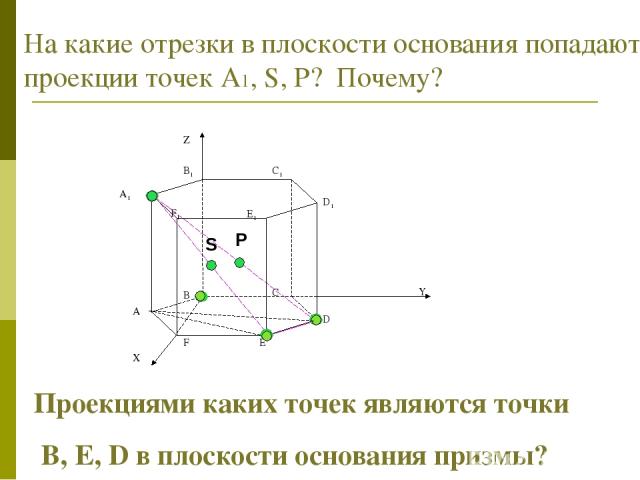
На какие отрезки в плоскости основания попадают проекции точек А1, S, Р? Почему? Проекциями каких точек являются точки B, E, D в плоскости основания призмы?

Составьте уравнение плоскости по 3 точкам:

Составьте самостоятельно уравнения координатных плоскостей

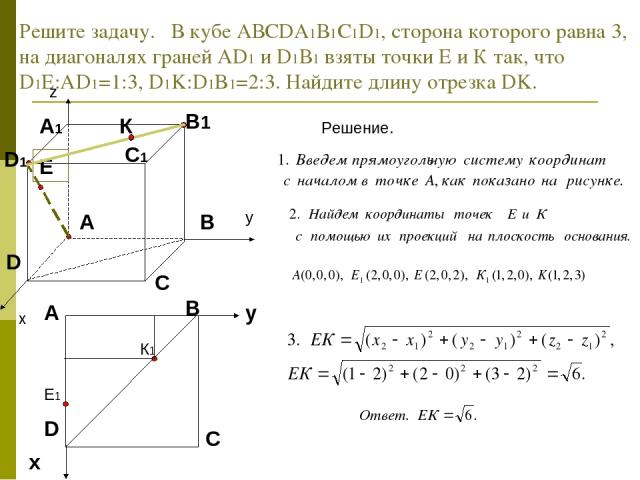
Решите задачу. В кубе АВСDА1В1С1D1, сторона которого равна 3, на диагоналях граней АD1 и D1В1 взяты точки Е и К так, что D1Е:АD1=1:3, D1K:D1B1=2:3. Найдите длину отрезка DK. Решение.

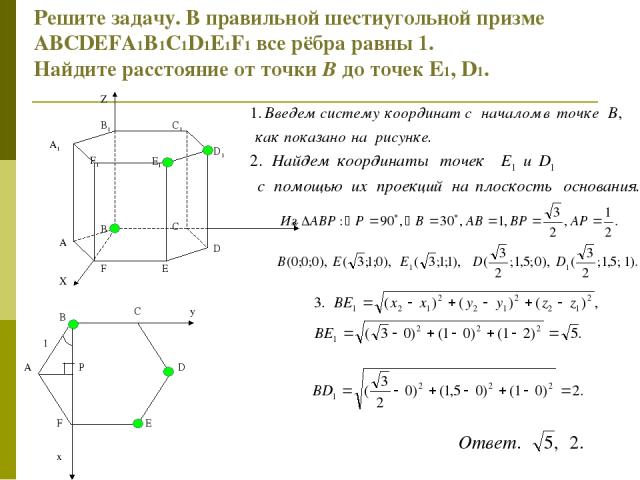
Решите задачу. В правильной шестиугольной призме  ABCDEFA1B1C1D1E1F1 все рёбра равны 1. Найдите расстояние от точки В до точек Е1, D1. y x

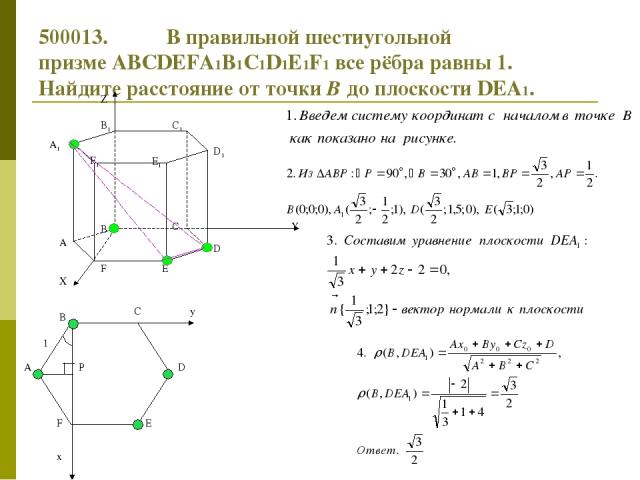
500013. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 1. Найдите расстояние от точки В до плоскости DEA1. y x

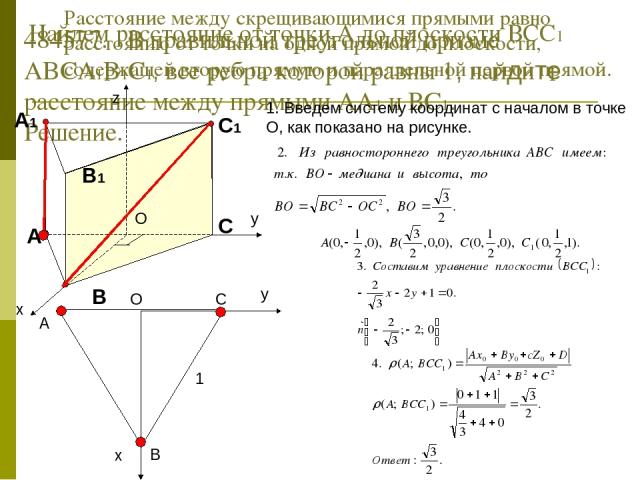
484577. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите расстояние между прямыми АА1 и ВС1. Решение. Расстояние между скрещивающимися прямыми равно расстоянию от точки на одной прямой до плоскости, содержащей вторую прямую и параллельной первой прямой. 1. Введем систему координат с началом в точке О, как показано на рисунке. Найдем расстояние от точки А до плоскости ВСС1

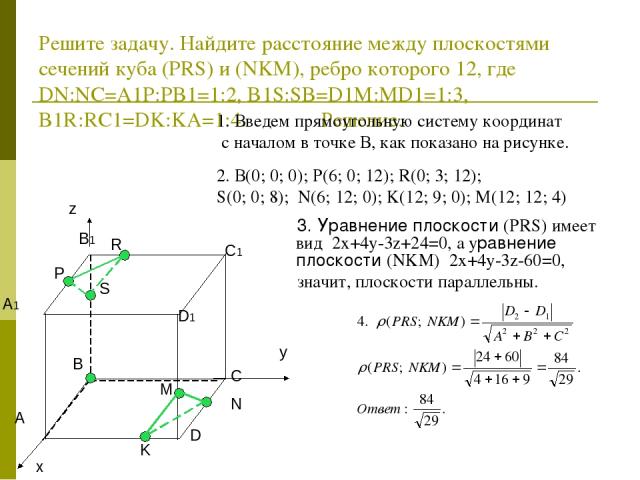
Решите задачу. Найдите расстояние между плоскостями сечений куба (PRS) и (NKM), ребро которого 12, где DN:NC=A1P:PB1=1:2, B1S:SB=D1M:MD1=1:3, B1R:RC1=DK:KA=1:4. Решение. 1. Введем прямоугольную систему координат с началом в точке В, как показано на рисунке. 2. В(0; 0; 0); P(6; 0; 12); R(0; 3; 12); S(0; 0; 8); N(6; 12; 0); K(12; 9; 0); M(12; 12; 4) 3. Уравнение плоскости (PRS) имеет вид 2x+4y-3z+24=0, а уравнение плоскости (NKM) 2x+4y-3z-60=0, значит, плоскости параллельны.

500387. На ребре  СС1 куба ABCDA1B1C1D1 отмечена точка E  так, что CE:EC1=2:1 . Найдите угол между прямыми  BE и AC1 .

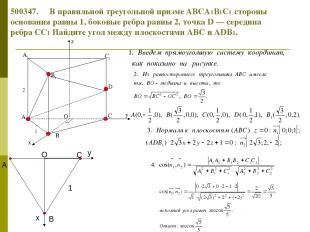
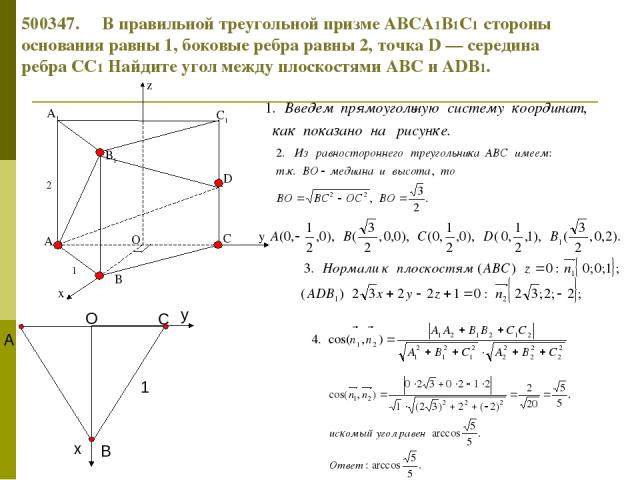
500347. В правильной треугольной призме ABCA1B1C1 стороны основания равны 1, боковые ребра равны 2, точка D — середина ребра CC1 Найдите угол между плоскостями ABC и ADB1.

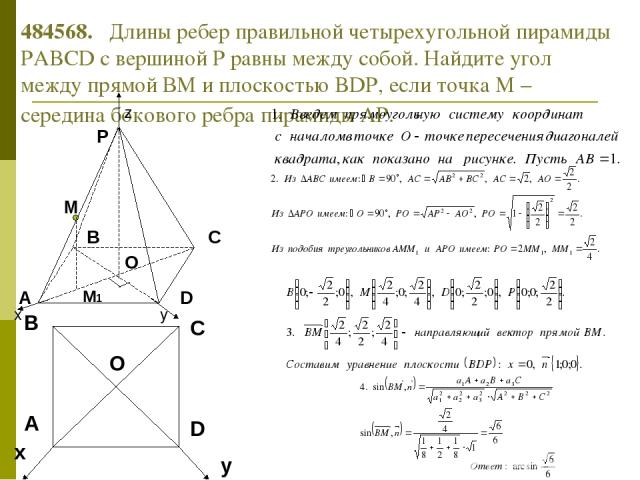
484568. Длины ребер правильной четырехугольной пирамиды PABCD с вершиной Р равны между собой. Найдите угол между прямой ВМ и плоскостью BDP, если точка М – середина бокового ребра пирамиды АР.

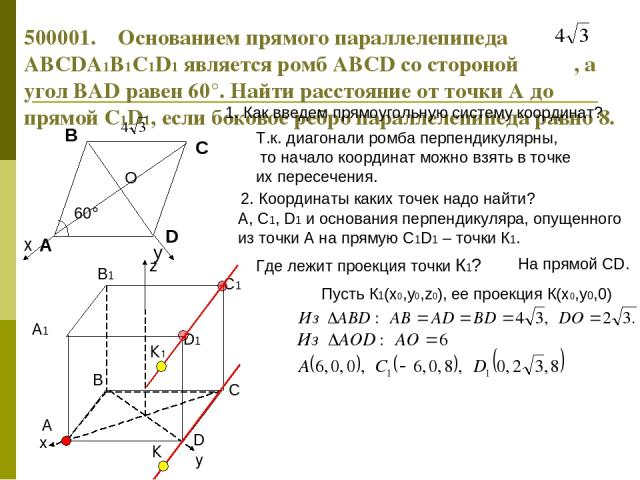
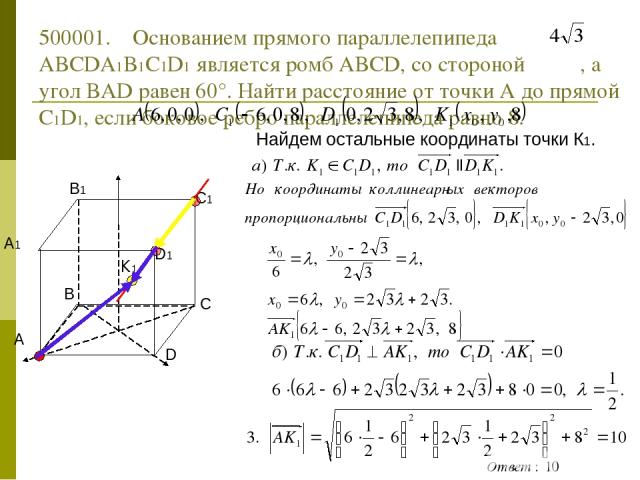
60° 500001. Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD со стороной , а угол BAD равен 60°. Найти расстояние от точки А до прямой С1D1, если боковое ребро параллелепипеда равно 8. 1. Как введем прямоугольную систему координат? Т.к. диагонали ромба перпендикулярны, то начало координат можно взять в точке их пересечения. 2. Координаты каких точек надо найти? А, С1, D1 и основания перпендикуляра, опущенного из точки А на прямую С1D1 – точки К1. Где лежит проекция точки К1? На прямой СD. Пусть К1(х0,у0,z0), ее проекция К(х0,у0,0)

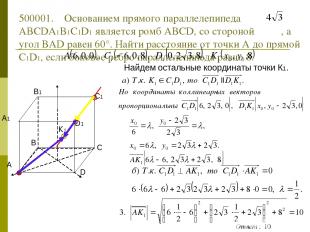
500001. Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, со стороной , а угол BAD равен 60°. Найти расстояние от точки А до прямой С1D1, если боковое ребро параллелепипеда равно 8. Найдем остальные координаты точки К1.

Домашнее задание: решите задачи по выбору 3. В единичном кубе ABCDA1B1C1D1 точки E и K – середины ребер AA1 и CD соответственно, а точка M расположена на диагонали B1D1 так, что B1M=2MD1. Найти расстояние между точками Q и L, где Q – середина отрезка ЕМ, а L – точка отрезка МК такая, что ML=2LK. 1. Ребра правильной четырехугольной призмы равны 1, 4, 4. Найти расстояние от вершины до центра основания призмы, не содержащего эту вершину. 2. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все рёбра равны 1. Найдите расстояние от точки В до точек Е1, D1. № 484559, 484569, 485992, 485997, 500007, 500193, 500367 на сайте http://reshuege.ru

При разработке презентации были использованы тексты задач 1. http://reshuege.ru – образовательный портал для подготовки к экзаменам. 2. www.alexlarin.narod.ru – сайт по оказанию информационной поддержки студентам и абитуриентам при подготовке к ЕГЭ, поступлению в ВУЗы и изучении различных разделов высшей математики. Литература Потоскуев Е.В. Геометрия 10 кл.: учеб. для общеобразоват. учреждений с углубленным и профильным изучением математики/ Е.В. Потоскуев, Л.И. Звавич. – 5-е изд., стереотип. – М.: Дрофа. 2007. – 223, [1]c.: ил.