Презентация на тему: Равнобедренный треугольник и его свойства

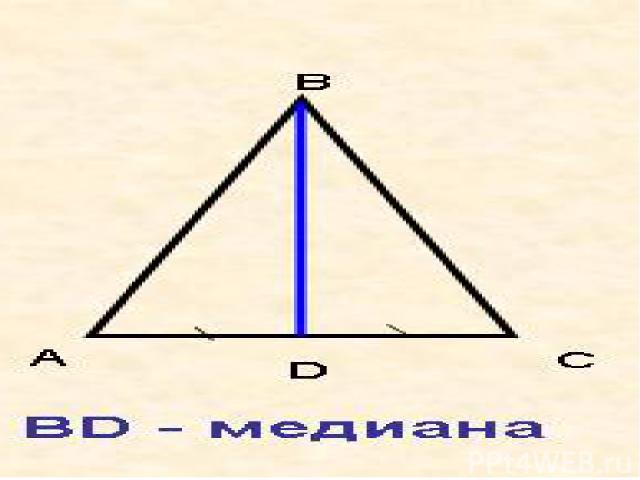
Свойство медианы равнобедренного треугольника. / \

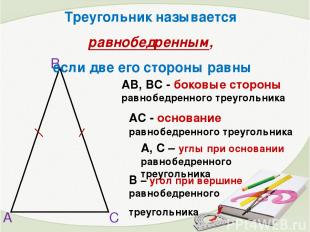
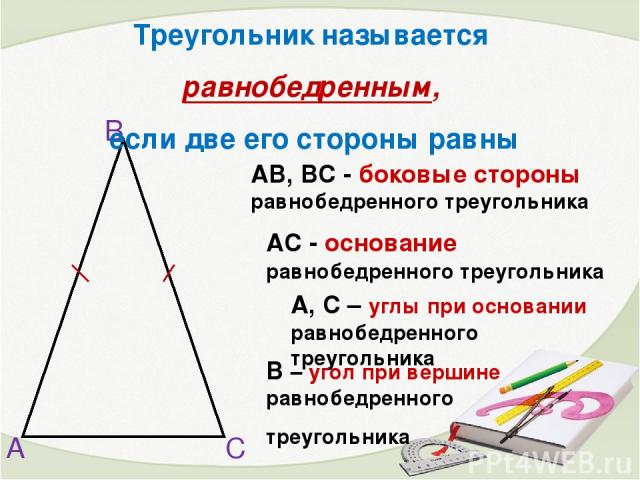
А В С АВ, ВС - боковые стороны равнобедренного треугольника А, С – углы при основании равнобедренного треугольника АС - основание равнобедренного треугольника В – угол при вершине равнобедренного треугольника Треугольник называется равнобедренным, если две его стороны равны

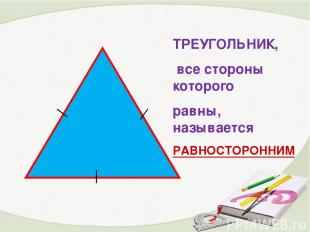
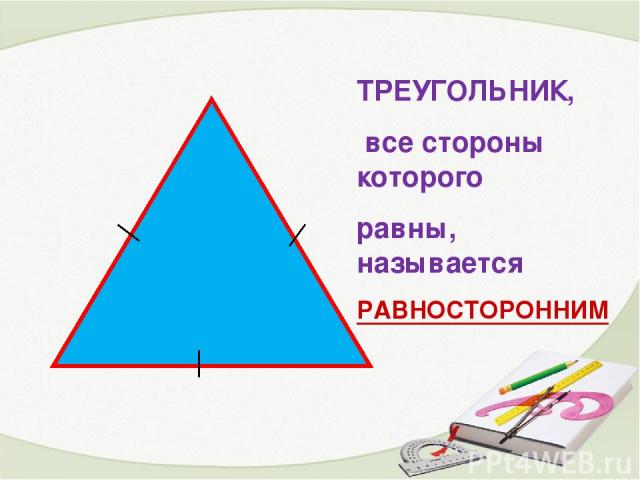
ТРЕУГОЛЬНИК, все стороны которого равны, называется РАВНОСТОРОННИМ

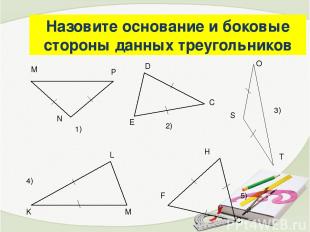
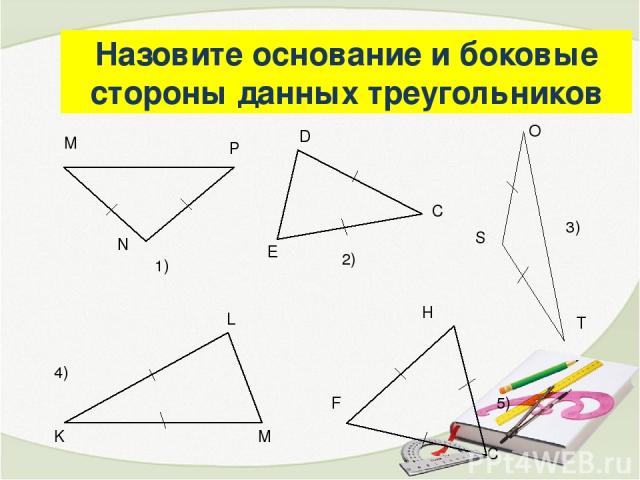
Назовите основание и боковые стороны данных треугольников

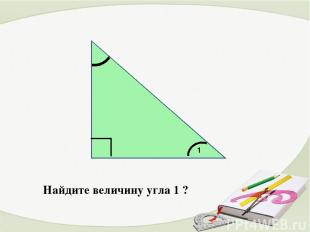
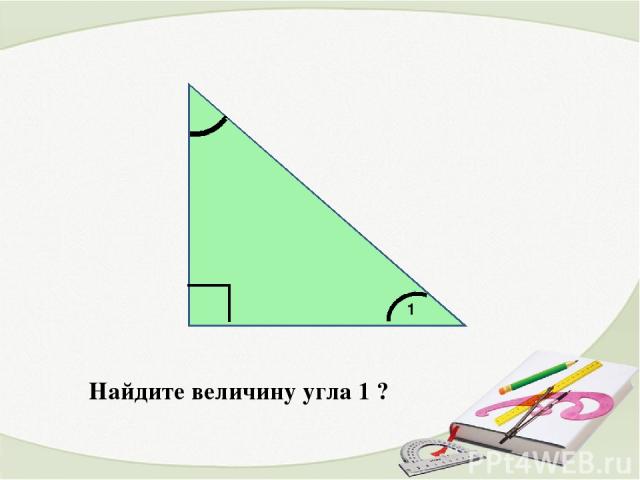
Найдите величину угла 1 ? 1

1 Найти величину угла 1, если величина угла 2 равна 40 град.? 2

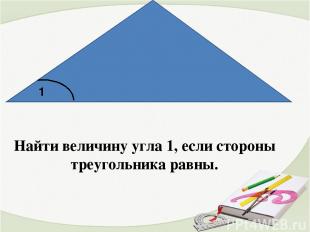
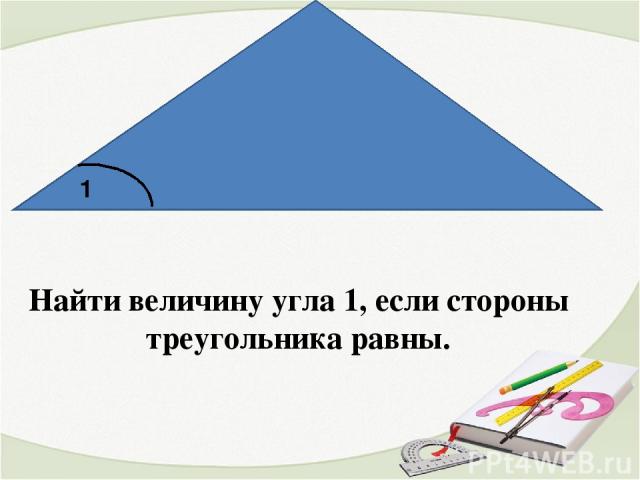
Найти величину угла 1, если стороны треугольника равны. 1

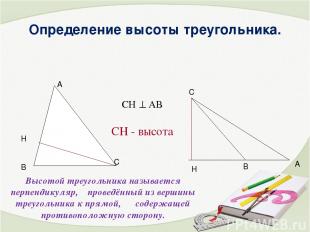
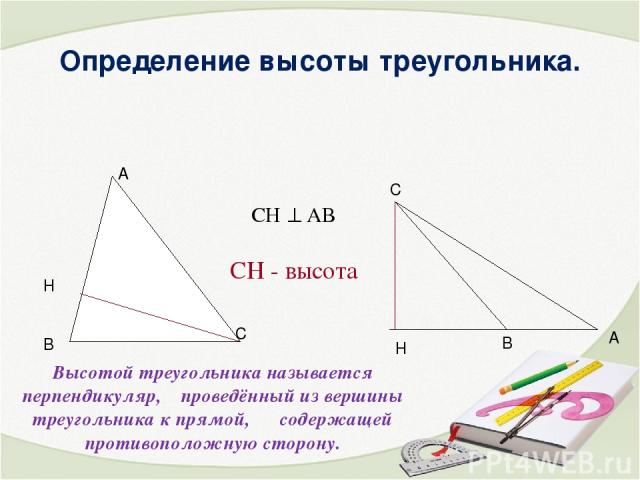
Определение высоты треугольника. Высотой треугольника называется перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону. СН - высота СН АВ

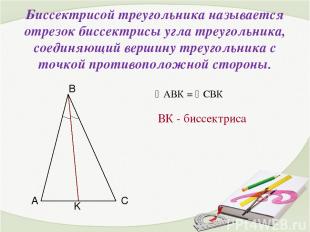
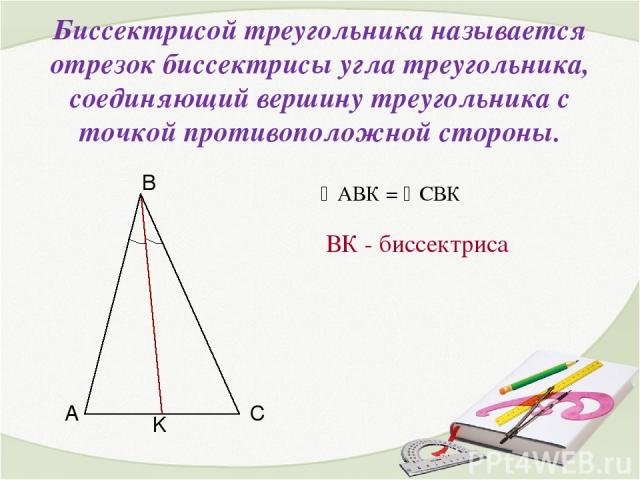
Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. ВК - биссектриса АВК = СВК

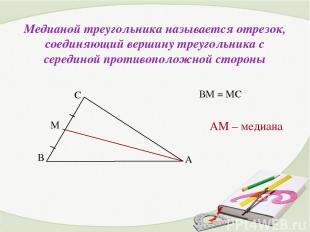
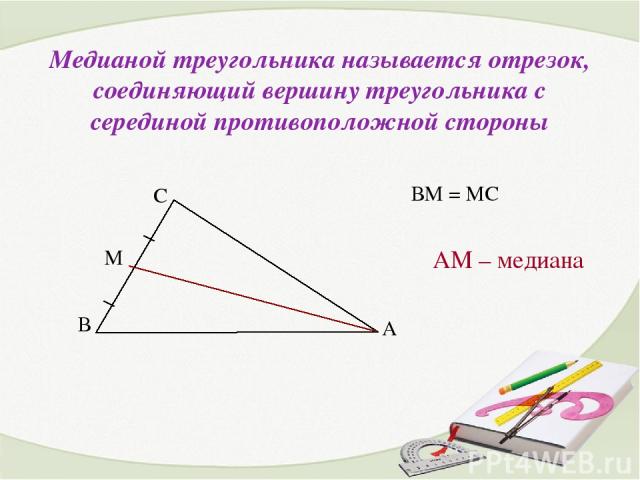
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны АМ – медиана ВМ = МС

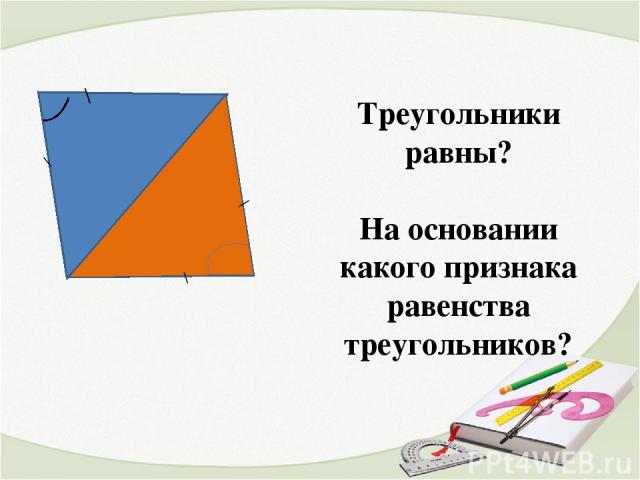
\ \ \ \ Треугольники равны? На основании какого признака равенства треугольников?

, 3 а

Меч диван а медиана

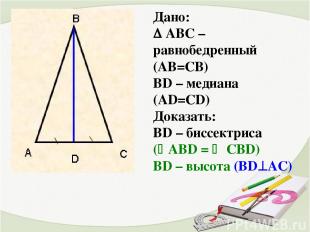
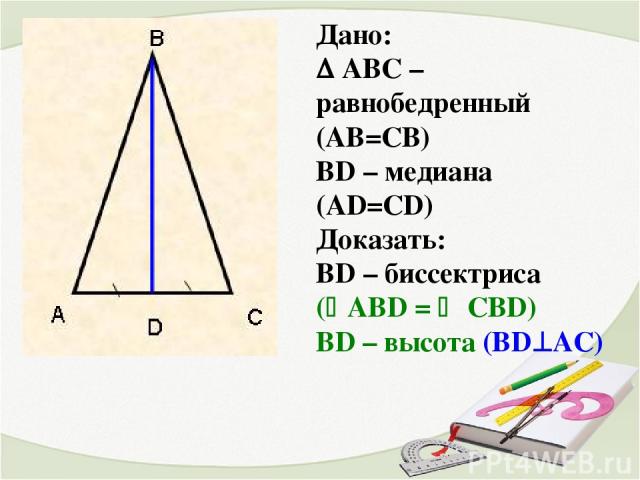
Дано: АВС – равнобедренный (АВ=СВ) ВD – медиана (AD=СD) Доказать: ВD – биссектриса ( AВD = CBD) ВD – высота (ВD AС)

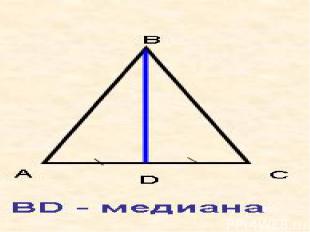
Доказательство: AВD = CBD (по первому признаку равенства треугольников), т.к. AД=CД (по условию) AВ=СB (треугольник АВС - равнобедренный) A = B (по свойству углов при основании равнобедренного треугольника) AВD = CBD ACD = BCD CD – биссектриса ADC = BDC ADC и BDC - смежные ADC = BDC = 90 CD AB CD – высота. Что и требовалось доказать.

Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой 2.Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.

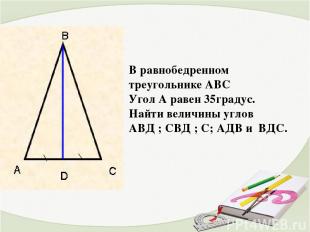
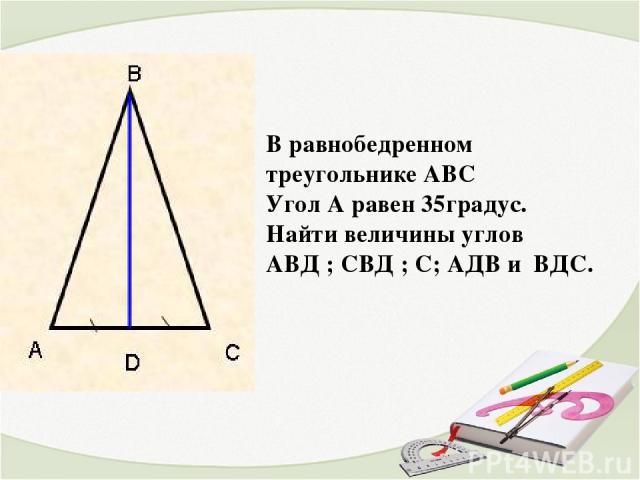
В равнобедренном треугольнике АВС Угол А равен 35градус. Найти величины углов АВД ; СВД ; С; АДВ и ВДС.

ТЕСТ.

Домашнее задание:  п.25-26, контрольные вопросы 8-11. Дома просмотреть презентацию. Записать в тетрадь формулировку и доказательство теоремы и сделать рисунок. • Творческое задание: из 6 спичек сделать 4 равносторонних треугольника.

Красивые здания, картины создаются с учетом принципа “золотого треугольника”. Все это построено на связанных между собой математических пропорциях, в сечении получается звезда, где пять равнобедренных треугольников, они называются “золотыми”.

Где в жизни встречаются равнобедренные треугольники? Для желающих: подготовить презентацию:• Крыши домов, башен; Орнаменты; Арки мостов; Египетские пирамиды; Северные росписи…

Оцените “уровень успешности”: Пришлите «5»— если вам все было понятно и вы справились с заданиями, «4»– если кое-что непонятно и «3»– если все непонятно и срочно нужна помощь.

Таблицы. Справочные материалы. (Дополнительный файл)