Презентация на тему: Равносторонний треугольник

900igr.net

Провести исследование, можно ли построить равносторонний треугольник на листе клеточной тетради с помощью линейки найти и изучить различные соотношения в равностороннем треугольнике выбрать наиболее интересные и представить их одноклассникам, и показать в своей работе

Посетили библиотеку, нашли необходимую научно-популярную литературу, прочли статьи в журналах «Квант» и «Математика в школе». Научились искать информацию в Интернете. Выбрали способы доказательства некоторых соотношений, используя дополнительные построения. Создали презентацию.

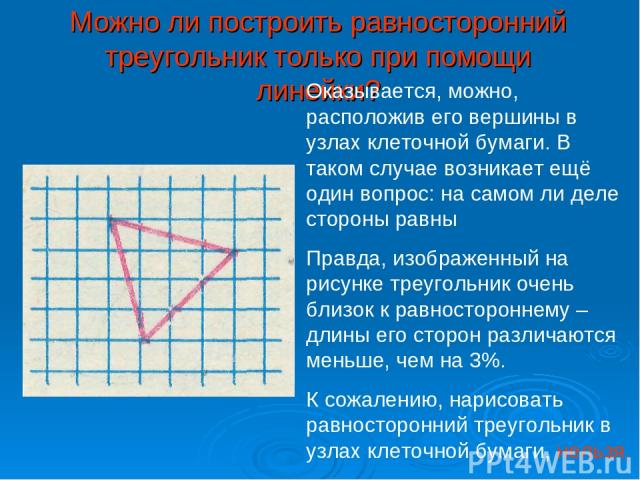
Можно ли построить равносторонний треугольник только при помощи линейки? Оказывается, можно, расположив его вершины в узлах клеточной бумаги. В таком случае возникает ещё один вопрос: на самом ли деле стороны равны Правда, изображенный на рисунке треугольник очень близок к равностороннему – длины его сторон различаются меньше, чем на 3%. К сожалению, нарисовать равносторонний треугольник в узлах клеточной бумаги, нельзя.

1 .Теперь возьмём т. Р внутри равностороннего треугольника и отпустим из неё на стороны перпендикуляры PE, PL, PF. Оказывается, что сумма этих отрезков не зависит от выбора т. Р и равняется высоте треугольника. A B C P E L F Дано: ∆ АВС – равносторонний h – высота, a - сторона РЕ, РL, PF – перпендикуляры Доказать: h = РF + PL + PE

A C B P E F L Проведем MN || AC, KD || AB, RS || BC. ∆KPS, ∆MPR , ∆NPD - равносторонние, т.к. прямые, параллельные сторонам правильного треугольника, образуют правильные треугольники. МР=АК, PN=SB, PD = RC т.к. замкнуты между параллельными прямыми и сами тоже параллельны. АК +КS + SB= AC, а потому и сумма высот этих треугольников равна высоте ∆ АВС, т.е. PE+ PL+ PF = h Что и требовалось доказать. М N K D M R S II способ

2 . Внутри равностороннего треугольника взята точка Р, и проведены перпендикуляры PE, PF, PL к сторонам этого треугольника. Сумма длин отрезков AF, BE и CL равна сумме длин отрезков CF, BL и AE. А В С Е L F P Дано: ∆ АВС – равносторонний Доказать: AF + CL + BE = CF + BL + AE

II способ. Проведем MN || AC, KD || AB, RS || BC. ∆KPS, ∆MPR , ∆NPD - равносторонние, т.к. прямые, параллельные сторонам правильного треугольника, образуют правильные треугольники. МР=АК, PN=SC, PD = RB, АМ=КР т.к. замкнуты между параллельными прямыми и сами тоже параллельны. АК +КS + SB= AC. Пусть АК=х, КS=y, SC=z, то АE=у+0,5х, ВL=х+0,5z, CF=z+0,5y AE+BL+CF= 1,5(x+y+z). AF=x+0,5y, CL=y+0,5z, BE=z+0,5x, тогда AF+CL+BE=1,5(x+y+z). Следовательно, AF+CL+BE=AE+BL+CF Что и требовалось доказать.

Если на сторонах произвольного треугольника во внешнюю сторону построить равносторонние треугольники, то их центры будут вершинами равностороннего треугольника. Этот факт верен и в том случае, если равносторонние треугольники строить внутрь данного.

Немецкий механик Франз Рело заметил, что если провести дуги окружностей с центрами в вершинах равностороннего треугольника, соединяющие две другие его вершины, то полученная (она получила название треугольник Реле) будет обладать свойством постоянства ширины, т.е. расстояние между двумя параллельными касательными к этой кривой будет постоянной величиной, равной стороне треугольника.

Равносторонний треугольник можно поворачивать внутри лупочки, составленной из двух дуг окружности, каждая из которых равняется 120, а радиус равен стороне треугольника. Если же взять лупочку из двух дуг вдвое меньшего размера (60), а радиус равен высоте треугольника, то такую лупочку можно вращать внутри этого треугольника, так, что она всё время будет касаться всех его сторон.

. Скопец З.А. «Геометрические миниатюры», М. «Просвещение», 1991 г. Биографический указатель ХРОНОСа http://www.hrono.ru/da/cd_rom.html Ж.«Квант» №5, М, «Наука», 1991 г. Н. Лэнгдон, Ч. Снейп, «С математикой в путь», М. «Педагогика», 1987 г. К. У. Шахно, «Сборник задач по элементарной математике повышенной трудности», Минск «Вышэйшая школа», 1968 г.