Презентация на тему: Площадь прямоугольного треугольника

Площадь прямоугольного треугольника уч-к Л.Г. Петерсон, 4-й класс, часть 1, урок 32 2 варианта подводящего диалога, решение задач Смирнова М.А. ГОУ ЦО 293, Москва

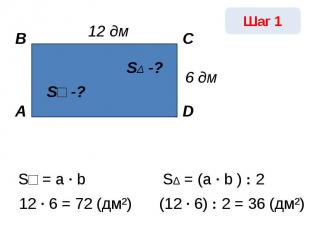
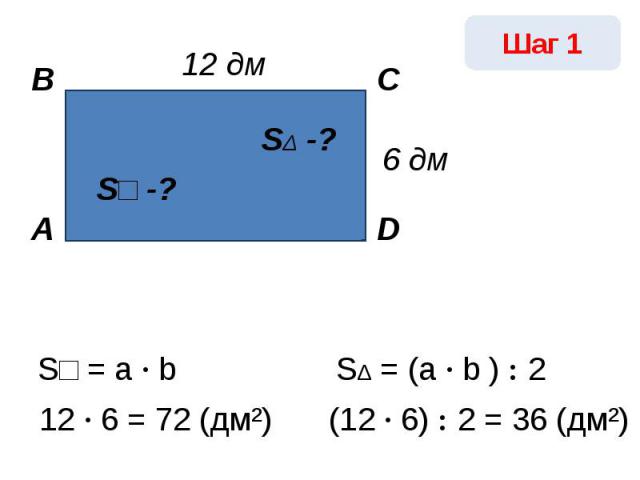
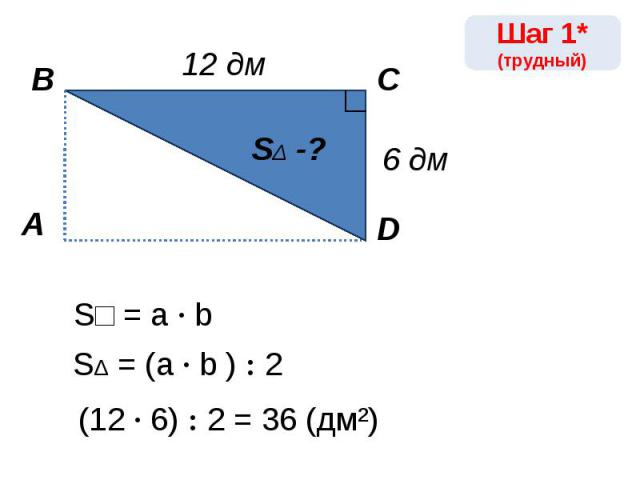
S□ = a · b 12 · 6 = 72 (дм²) SΔ = (a · b ) : 2(12 · 6) : 2 = 36 (дм²)

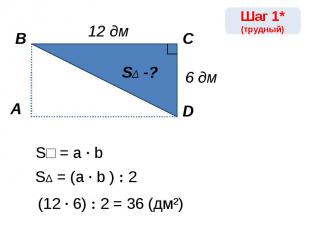
S□ = a · bSΔ = (a · b ) : 2(12 · 6) : 2 = 36 (дм²)

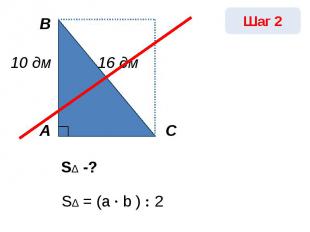
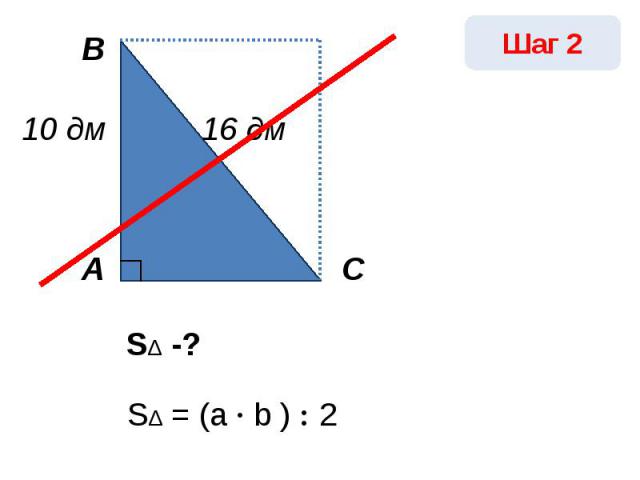
SΔ -?SΔ = (a · b ) : 2

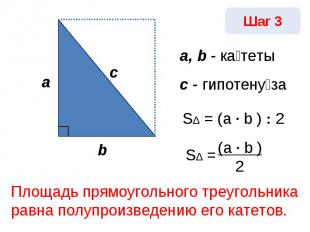
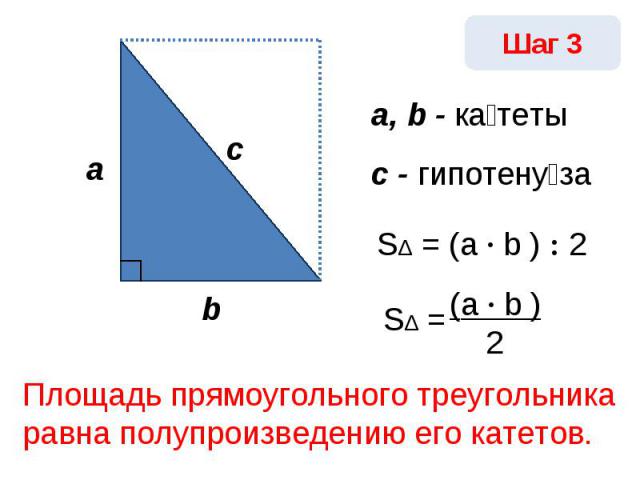
Площадь прямоугольного треугольника равна полупроизведению его катетов.

Решение задач из учебника Л.Г. Петерсон, 4 класс

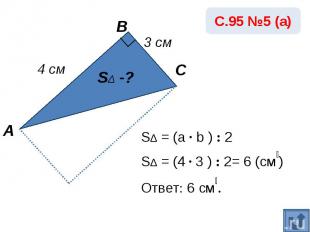
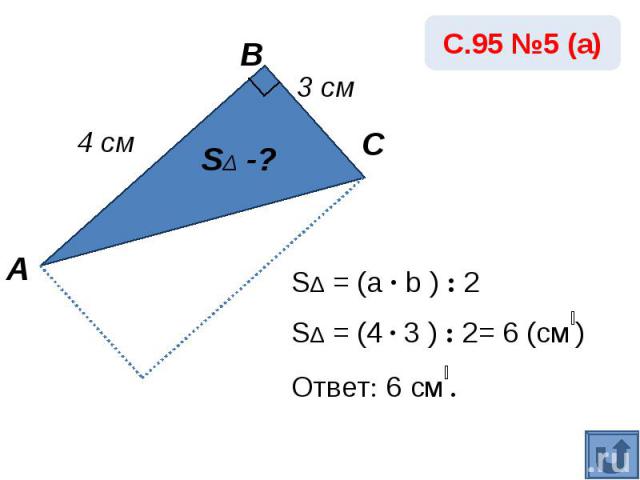
SΔ = (a · b ) : 2SΔ = (4 · 3 ) : 2= 6 (см₂)Ответ: 6 см₂.

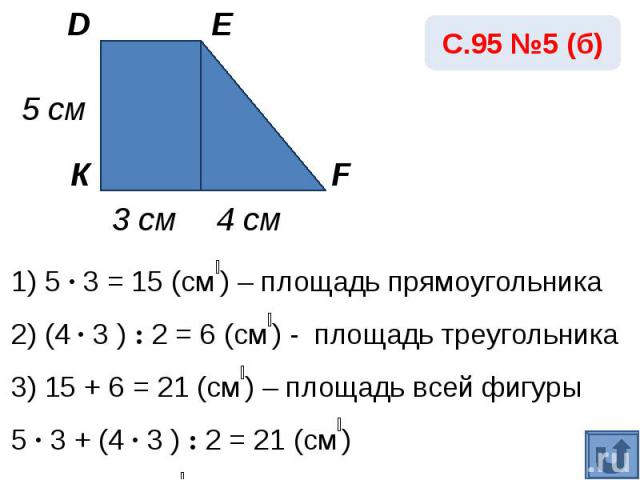
С.95 №5 (б)1) 5 · 3 = 15 (см₂) – площадь прямоугольника2) (4 · 3 ) : 2 = 6 (см₂) - площадь треугольника3) 15 + 6 = 21 (см₂) – площадь всей фигуры5 · 3 + (4 · 3 ) : 2 = 21 (см₂)Ответ: 21 см₂.

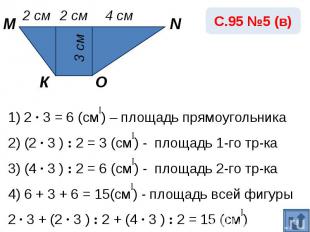
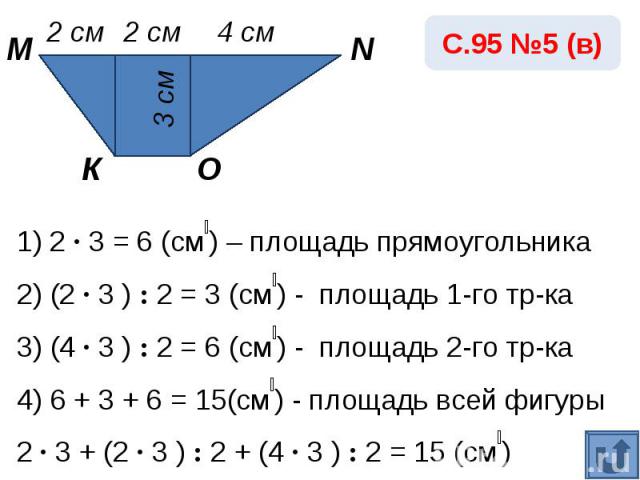
1) 2 · 3 = 6 (см₂) – площадь прямоугольника2) (2 · 3 ) : 2 = 3 (см₂) - площадь 1-го тр-ка3) (4 · 3 ) : 2 = 6 (см₂) - площадь 2-го тр-ка4) 6 + 3 + 6 = 15(см₂) - площадь всей фигуры2 · 3 + (2 · 3 ) : 2 + (4 · 3 ) : 2 = 15 (см₂)Ответ: 15 см₂.

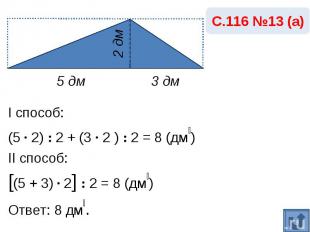
С.116 №13 (а)I способ:(5 · 2) : 2 + (3 · 2 ) : 2 = 8 (дм₂)II способ:[(5 + 3) · 2] : 2 = 8 (дм₂)Ответ: 8 дм₂.

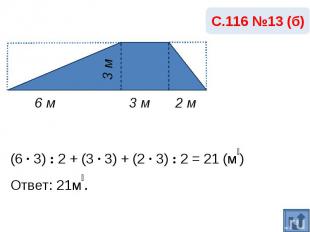
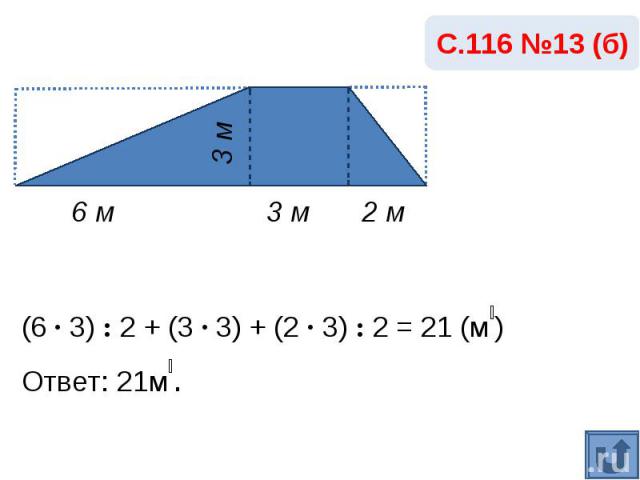
С.116 №13 (б)(6 · 3) : 2 + (3 · 3) + (2 · 3) : 2 = 21 (м₂)Ответ: 21м₂.

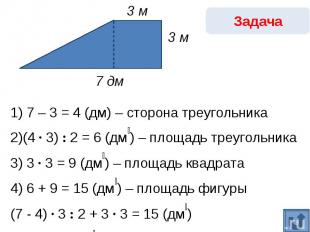
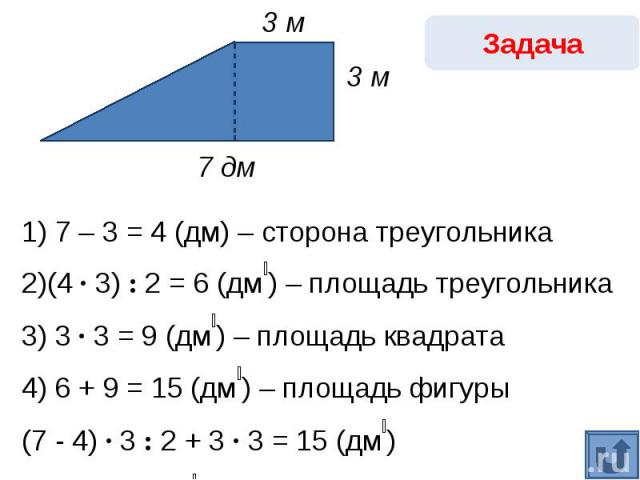
Задача1) 7 – 3 = 4 (дм) – сторона треугольника2)(4 · 3) : 2 = 6 (дм₂) – площадь треугольника3) 3 · 3 = 9 (дм₂) – площадь квадрата4) 6 + 9 = 15 (дм₂) – площадь фигуры(7 - 4) · 3 : 2 + 3 · 3 = 15 (дм₂) Ответ: 15 дм₂.

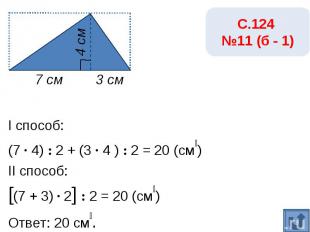
С.124 №11 (б - 2)I способ:(1 · 4) : 2 + (9 · 4 ) : 2 = 20 (см₂)II способ:[(1 + 9) · 4] : 2 = 20 (см₂)Ответ: 20 см₂.

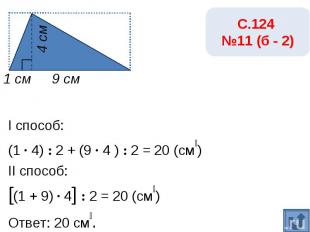
С.124 №11 (б - 2)I способ:(1 · 4) : 2 + (9 · 4 ) : 2 = 20 (см₂)II способ:[(1 + 9) · 4] : 2 = 20 (см₂)Ответ: 20 см₂.

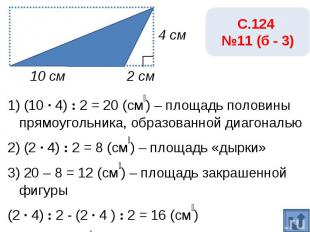
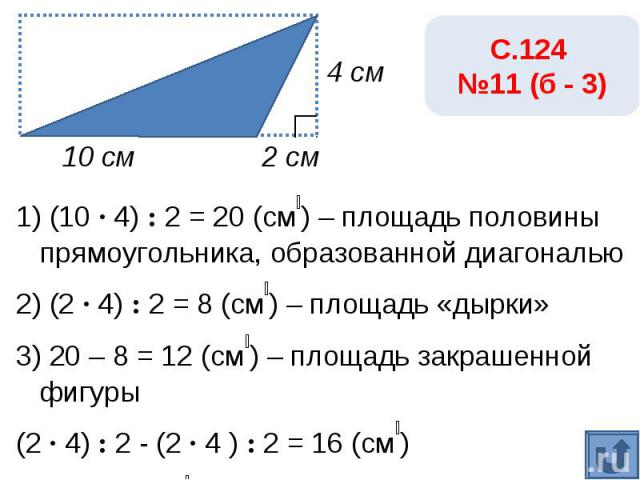
С.124 №11 (б - 3)1) (10 · 4) : 2 = 20 (см₂) – площадь половины прямоугольника, образованной диагональю2) (2 · 4) : 2 = 8 (см₂) – площадь «дырки»3) 20 – 8 = 12 (см₂) – площадь закрашенной фигуры(2 · 4) : 2 - (2 · 4 ) : 2 = 16 (см₂)Ответ: 20 см₂.

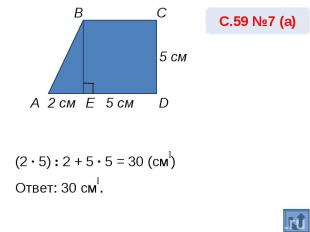
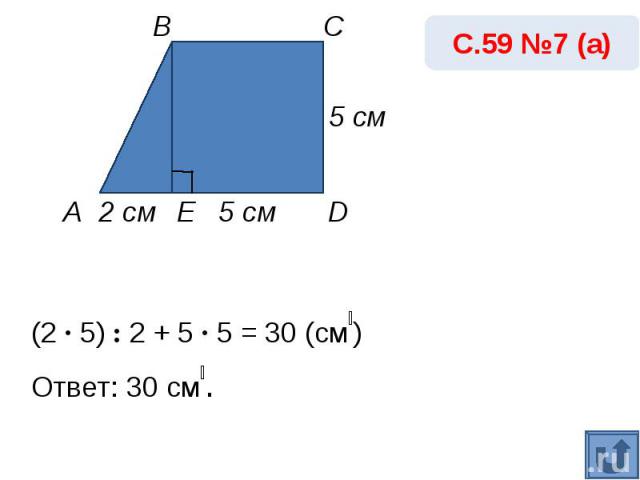
(2 · 5) : 2 + 5 · 5 = 30 (cм₂) Ответ: 30 cм₂.

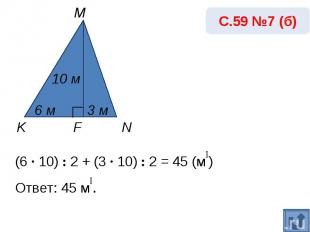
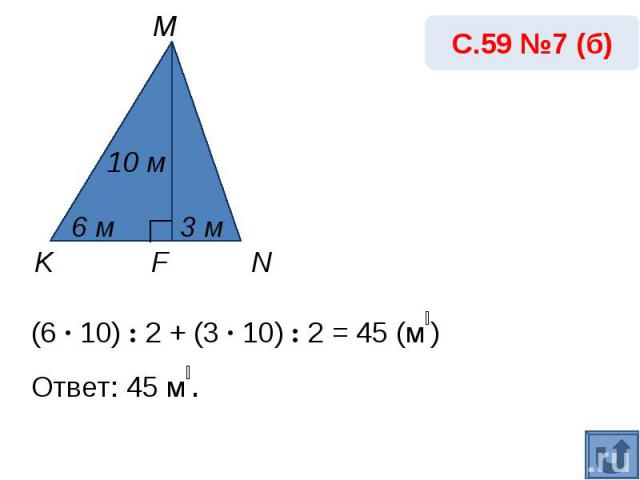
С.59 №7 (б)(6 · 10) : 2 + (3 · 10) : 2 = 45 (м₂) Ответ: 45 м₂.

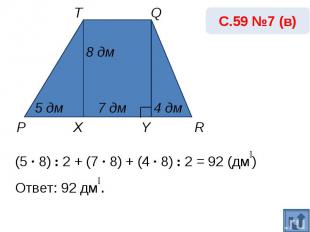
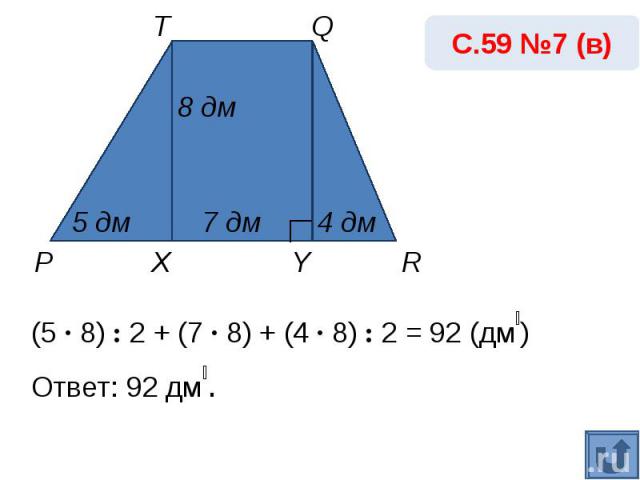
С.59 №7 (в)(5 · 8) : 2 + (7 · 8) + (4 · 8) : 2 = 92 (дм₂) Ответ: 92 дм₂.