Презентация на тему: Многогранник

МНОГОГРАННИК – ЭТО ПОВЕРХНОСТЬ, СОСТАВЛЕННАЯ ИЗ МНОГОУГОЛЬНИКОВ И ОГРАНИЧИВАЮЩАЯ ГЕОМЕТРИЧЕСКОЕ ТЕЛО. ЭТО ТЕЛО ТАКЖЕ НАЗЫВАЮТ МНОГОГРАННИКОМ. Октаэдр Прямоугольный параллелепипед Тетраэдр Куб

МНОГОГРАННИКИ Многоугольники, из которых составлен многогранник, называются гранями. Стороны граней называются рёбрами. А концы рёбер называют вершинами многоугольника. Гранью куба является квадрат А В АВ является ребром куба А А является вершиной куба

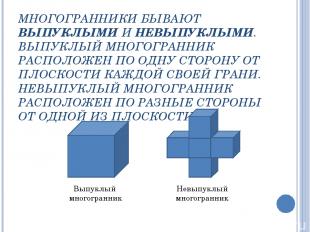
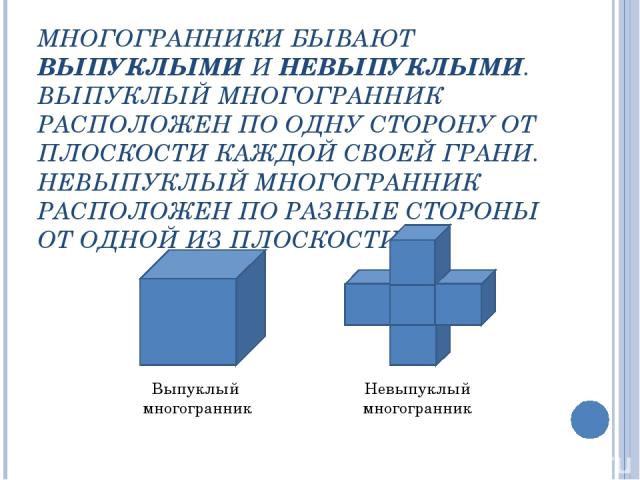
МНОГОГРАННИКИ БЫВАЮТ ВЫПУКЛЫМИ И НЕВЫПУКЛЫМИ. ВЫПУКЛЫЙ МНОГОГРАННИК РАСПОЛОЖЕН ПО ОДНУ СТОРОНУ ОТ ПЛОСКОСТИ КАЖДОЙ СВОЕЙ ГРАНИ. НЕВЫПУКЛЫЙ МНОГОГРАННИК РАСПОЛОЖЕН ПО РАЗНЫЕ СТОРОНЫ ОТ ОДНОЙ ИЗ ПЛОСКОСТИ. Выпуклый многогранник Невыпуклый многогранник

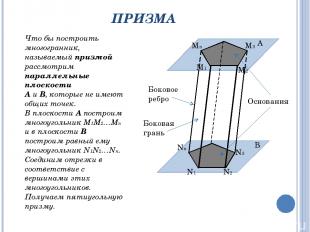
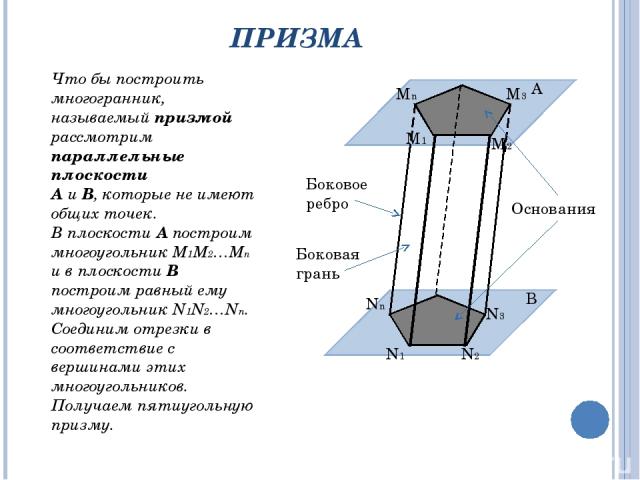
ПРИЗМА Что бы построить многогранник, называемый призмой рассмотрим параллельные плоскости А и В, которые не имеют общих точек. В плоскости А построим многоугольник М1М2…Мn и в плоскости В построим равный ему многоугольник N1N2…Nn. Соединим отрезки в соответствие с вершинами этих многоугольников. Получаем пятиугольную призму. А В M1 M2 M3 Mn Nn N1 N2 N3 Боковое ребро Боковая грань Основания

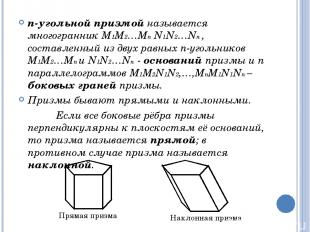
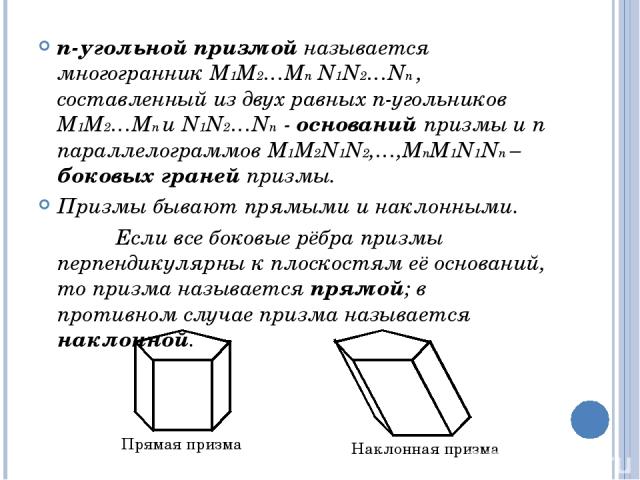
n-угольной призмой называется многогранник М1М2…Мn N1N2…Nn , составленный из двух равных n-угольников М1М2…Мn и N1N2…Nn - оснований призмы и n параллелограммов М1М2N1N2,…,МnМ1N1Nn – боковых граней призмы. Призмы бывают прямыми и наклонными. Если все боковые рёбра призмы перпендикулярны к плоскостям её оснований, то призма называется прямой; в противном случае призма называется наклонной. Прямая призма Наклонная призма

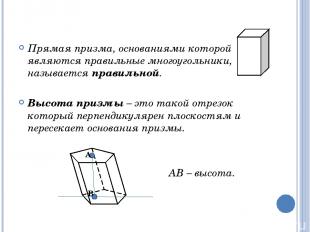
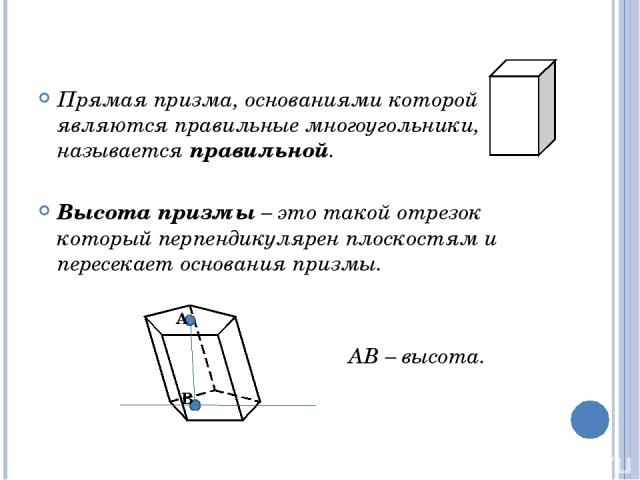
Прямая призма, основаниями которой являются правильные многоугольники, называется правильной. Высота призмы – это такой отрезок который перпендикулярен плоскостям и пересекает основания призмы. АВ – высота. А В

КОНЕЦ