Презентация на тему: Многогранник 3

В мире правильных многогранников Вклад философов-математиков в развитие теории многогранников Работу выполнили учащиеся 10 класса «А» МОУ СОШ № 107 Кузнецова Ольга, Иванова Елена 900igr.net

Математика: лабиринты открытий. Стереометрия как наука известна уже очень давно. Изысканиями в этой области занимались многие видные умы древности. Причём издавна великие «геометры» уделяли внимание не только теоретическим положениям и практическим приложениям науки, многие понятия, образы становились незаменимыми «компонентами» их философских систем. Мы рассмотрим вклад некоторых математиков в развитие «теории многогранников».

Цель исследования Выявить научный вклад в развитие теории многогранников философов-математиков Платона, Евклида, Аристотеля, Кеплера.

Проблема исследования Изучение многогранников на протяжении всей истории велось не только с позиций дальнейшего их применения, но и с целью осмысления философских вопросов об устройстве Вселенной и природе Пространства

Актуальность исследования Мы считаем необходимым проведение этого исследования, так как Мы интересуемся историей математики и хотели бы быть более просвещёнными в этой области. Это исследование помогло бы привлечь внимание окружающих к истории математики, науки, философии.

Ход исследования Анализ литературы по заявленной проблеме. Реферирование литературы. Создание презентации исследования. Представление результатов на научно-практической конференции. Обсуждение вопросов исследования на конференции.

Платон около 429 – 347 гг до н.э. Платоновыми телами называются правильные однородные выпуклые многогранники, то есть выпуклые многогранники, все грани и углы которых равны, причем грани - правильные многоугольники. Платоновы тела - трехмерный аналог плоских правильных многоугольников. Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников. Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются "Начала" Евклида.

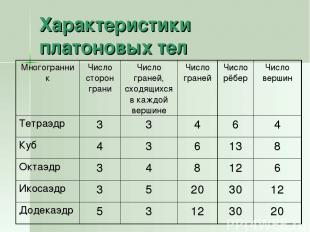
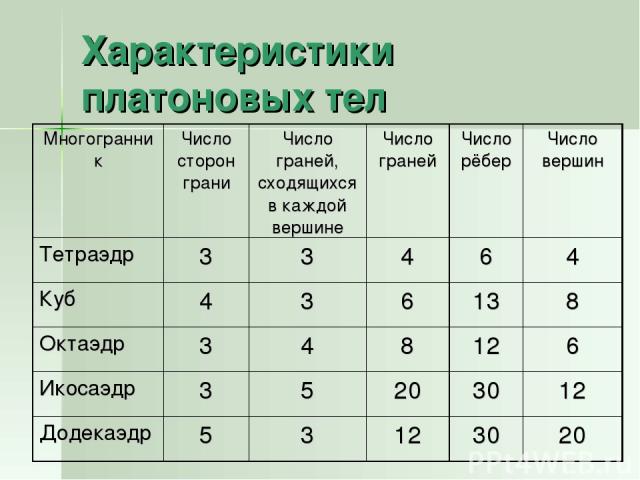
Характеристики платоновых тел

Платоновы тела

«Начала Евклида. «…в науке нет царского пути» около 365 – 300 гг. до н.э. Главный труд Евклида – «Начала» (в оригинале «Стохейа». «Начала» состоят из 13 книг, позднее к ним были прибавлены ещё 2. Первые шесть книг посвящены планиметрии. Книги VII – X содержат теорию чисел, XI, XII и XIII книги «Начал» посвящены стереометрии. Из постулатов Евклида видно, что он представлял пространство как пустое, безграничное, изотропное и трёхмерное. Интересно, что «Начала» Евклида открываются описанием построения правильного треугольника и заканчиваются изучением пяти правильных многогранных тел! В наше время они известны как платоновы тела.

Архимед Сиракузский около 287 – 212 гг. до н.э. Математик, физик и инженер Архимед Сиракузский оставил после себя немало изобретений, тринадцать сочинений (таких как «О сфере и цилиндре», «Измерение круга», «Равновесие плоскостей», «Стомахион», «Правильный семиугольник и другие). Архимед, как геометр определил поверхность шара и его объём, исследовал параболоиды и гиперболоиды, изучал «архимедову спираль», определил число «пи», как находящееся между 3,141 и 3,142. Вклад Архимеда в теорию многогранников - описание 13 полуправильных выпуклых однородных многогранников (архимедовых тел).

Архимедовы тела Множество архимедовых тел можно разбить на несколько групп. Первую из них составят пять многогранников, которые получаются из платоновых тел в результате их  усечения. Так могут быть получены пять архимедовых тел: усечённый тетраэдр, усечённый гексаэдр (куб), усечённый октаэдр, усечённый додекаэдр и усечённый икосаэдр. Другую группу составляют всего два тела, именуемых также квазиправильными многогранниками. Эти два тела носят названия:кубооктаэдр и икосододекаэдр Два последующих многогранника называются ромбокубооктаэдром и ромбоикосододекаэдром. Иногда их называют также «малым ромбокубооктаэдром» и «малым ромбоикосододекаэдром» в отличие от большого ромбокубооктаэдра и большого ромбоикосододекаэдра. Наконец существуют две так называемые «курносые» модификации — одна для куба, другая — для додекаэдра. Для каждой из них характерно несколько повёрнутое положение граней, что даёт возможность построить два различных варианта одного и того же «курносого» многогранника (каждый из них представляет собой как бы зеркальное отражение другого).

Иоганн Кеплер 1571 – 1630 гг. Немецкий астроном и математик. Один из создателей современной астрономии. Вклад Кеплера в теорию многогранника - это, во-первых, восстановление математического содержания утерянного трактата Архимеда о полуправильных выпуклых однородных многогранниках. Еще более существенным было предложение Кеплера рассматривать невыпуклые многогранники со звездчатыми гранями, подобными пентаграмме и последовавшее за этим открытие двух правильных невыпуклых однородных многогранников - малого звездчатого додекаэдра и большого звездчатого додекаэдра.

Космологическая гипотеза Кеплера Кеплер предположил, что расстояния между шестью известными тогда планетами выражаются через размеры пяти правильных выпуклых многогранников (Платоновых тел). Между каждой парой "небесных сфер", по которым, согласно этой гипотезе, вращаются планеты, Кеплер вписал одно из Платоновых тел. Весьма оригинальна космологическая гипотеза Кеплера, в которой он попытался связать некоторые свойства Солнечной системы со свойствами правильных многогранников.

Космологическая гипотеза Кеплера Вокруг сферы Меркурия, ближайшей к Солнцу планеты, описан октаэдр. Этот октаэдр вписан в сферу Венеры, вокруг которой описан икосаэдр. Вокруг икосаэдра описана сфера Земли, а вокруг этой сферы - додекаэдр. Додекаэдр вписан в сферу Марса, вокруг которой описан тетраэдр. Вокруг тетраэдра описана сфера Юпитера, вписанная в куб. Наконец, вокруг куба описана сфера Сатурна. Позже, с открытием еще трех планет и более точным измерением расстояний, эта гипотеза была полностью отвергнута.

Выводы Наше исследование показало, что проблема исследования многогранников была насущной всегда. Философы-математики в попытке описать и объяснить устройство Вселенной и природу пространства обращались к понятию многогранников. Таким образом математическое понятие «многогранники» становится своего рода философской категорией. Всякая научная гипотеза, даже неверная, способствует в конечном итоге общему научному прогрессу.

Литература Чанышев А.Н. Курс лекция по древней и средневековой философии: Учеб. Пособие для вузов. – М.: Высш. шк., 1991. – 512 с. Философия: Учебник для высших учебных заведений. – Ростов н/Д.: «Феникс», 1998 – 576 с. А также материалы сайтов http://pirog13.narod.ru/i.htm http://www.nips.riss-telecom.ru/poly/people