Презентация на тему: Метод координат на плоскости

МЕТОД КООРДИНАТ на плоскости 1. Координатная ось 2.Прямоугольная система координат на плоскости 3.Расстояния между точками 4.Координаты середины отрезка 5.Определение тригонометрических функций для любого угла 6.Применение координатной плоскости при решении алгебраических задач 7.Применение координатной плоскости при решении геометрических задач 900igr.net

1. Координатная ось Координатной осью называется прямая, на которой отмечена точка О (начало отсчета или начало координат), выбран масштаб, т.е. указан отрезок единичной длины для измерения расстояний (единичный или масштабный отрезок), и задано положительное направление. Так на рисунке 1 единичный отрезок на координатной оси Ох обозначен OE, направление от точки О к точке Е считается положительным (показано стрелкой). Начало координат О делит координатную ось на два луча: положительную полуось (которой принадлежит точка Е) и отрицательную полуось. Координатой точки Р, лежащей на оси Ох, называется число х = ±ОР (где ОР означает длину отрезка ОР), взятое со знаком плюс, если точка Р лежит на положительной полуоси, и со знаком минус, если эта точка лежит на отрицательной полуоси. Координату точку обычно указывают в скобках рядом с обозначением точки: Р (х). Между точками на числовой оси и их координатами имеется взаимно однозначное соответствие. Расстояние между двумя точками Р1 (х1) и Р2(х2) на оси Ох выражается формулой т.е. оно равно модулю разности соответствующих координат.

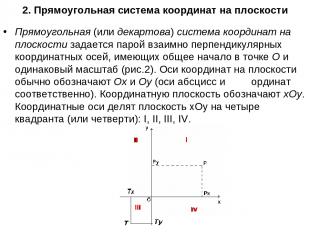
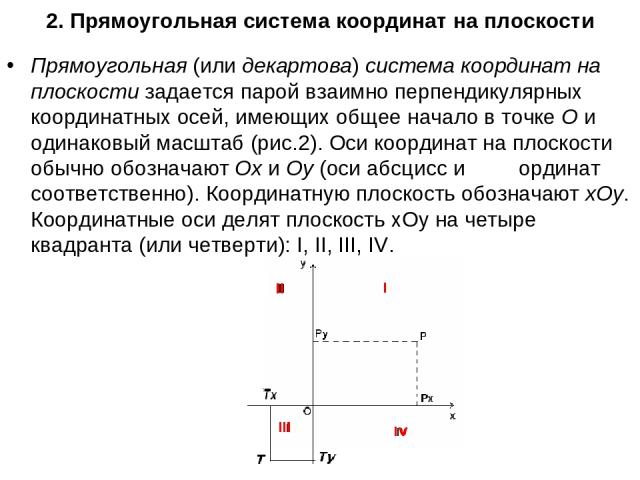
2. Прямоугольная система координат на плоскости Прямоугольная (или декартова) система координат на плоскости задается парой взаимно перпендикулярных координатных осей, имеющих общее начало в точке О и одинаковый масштаб (рис.2). Оси координат на плоскости обычно обозначают Ох и Оу (оси абсцисс и ординат соответственно). Координатную плоскость обозначают хОу. Координатные оси делят плоскость хОу на четыре квадранта (или четверти): I, II, III, IV.

Пусть точка Р лежит на плоскости хОу (рис.2). Опустим из этой точки перпендикуляры на координатные оси; основания перпендикуляров обозначим Рх и Ру. Абсциссой точки Р называется координата х точки Рх на оси Ох, ординатой – координата у точки Ру на оси Оу. Координаты точки обычно указывают в скобках рядом с обозначением точки: Р (х; у). Между точками на плоскости и их координатами имеется взаимно однозначное соответствие.

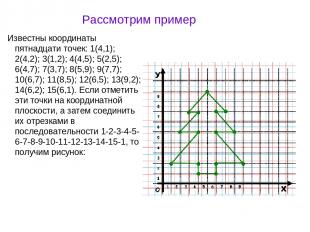
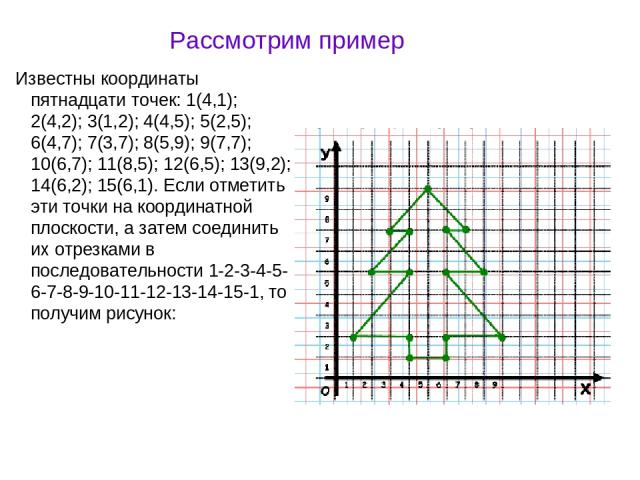
Рассмотрим пример Известны координаты пятнадцати точек: 1(4,1); 2(4,2); 3(1,2); 4(4,5); 5(2,5); 6(4,7); 7(3,7); 8(5,9); 9(7,7); 10(6,7); 11(8,5); 12(6,5); 13(9,2); 14(6,2); 15(6,1). Если отметить эти точки на координатной плоскости, а затем соединить их отрезками в последовательности 1-2-3-4-5-6-7-8-9-10-11-12-13-14-15-1, то получим рисунок:

Задача 1 Даны точки A(0; - 2), B(- 2;1), C(0;0) и D(2; - 9). Укажите те из них, которые лежат на прямой 2x - 3y + 7 = 0. Решение Уравнению прямой удовлетворяют координаты только точки B, т.к. 2(-2)- 3(1)+7=0, -4-3+7=0, 0=0

3. Расстояние между точками Пусть на плоскости хОу даны две точки: A1с координатами(x1;y1;) , и A2 с координатами(x2;y2) , . Выразим расстояние между точками и А через координаты этих точек. Рис.3 Рассмотрим сначала случай, когда х ≠ х1 и у ≠ у1. Проведем через точки А и А2прямые, параллельные осям координат , и обозначим точку их пересечения буквой А (рис.3). Расстояние между точками А и А 1 равно ׀у2-у 1 ׀, а расстояние между точками А и А 2 равно ׀х1-х 2 ׀. Применяя к прямоугольному треугольнику АА1А2 теорему Пифагора, получим: , откуда 1) , где d – расстояние между точками А и А.

Хотя формула (1) для расстояния между точками выведена нами в предположении х ≠ х1, у ≠ у 1, она остается верной и в других случаях. Действительно, если х = х 1, у ≠ у 1, то d равно ׀у – у 1 ׀. Тот же результат дает формула (1). Аналогично рассматривается случай, когда х ≠ х 1, у = у 1. При х = х 1, у = у 1 точки А и А 1 совпадают и формула (1) дает d = 0.

Задача 2 Даны точки A(0;0), B(- 2;1), C(3;3), D(2; - 1) и окружность (x - 1)2 + (y + 3)2 = 25. Выясните, где расположены эти точки: на окружности, внутри или вне окружности. Решение Подставив координаты данных точек в левую часть уравнения данной окружности, найдём квадраты расстояний от данных точек до центра Q(1; - 3) окружности: QA2 = (0 - 1) 2 + (0 + 3) 2 = 10 < 25, QB2 = (- 2 - 1) 2 + (1 + 3) 2 = 25, QC2 = (3 - 1) 2 + (3 + 3) 2 = 40 > 25, QD2 = (2 - 1) 2 + (- 1 + 3) 2 = 5 < 25. Следовательно, точки A и D расположены внутри окружности, точка B — на окружности, а точка C — вне окружности.

Задача 3 Найти расстояние между точками А (-1; -2) и В (-4; 2). Решение. По формуле (1) имеем:

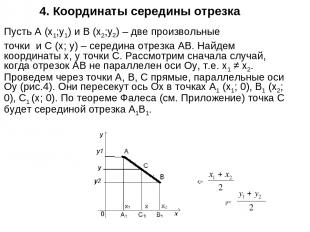
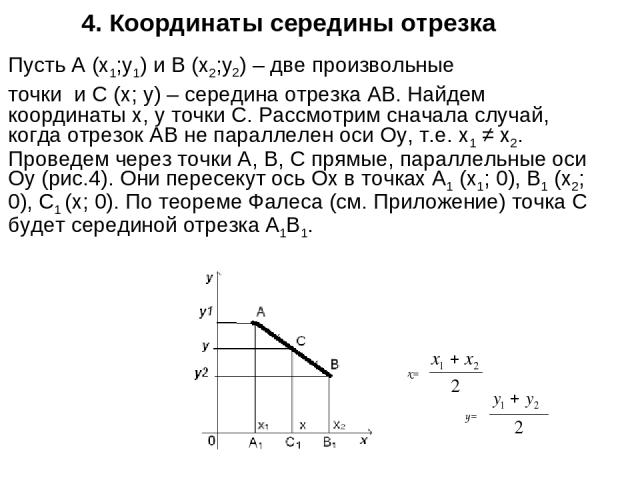
4. Координаты середины отрезка Пусть А (х1;у1) и В (х2;у2) – две произвольные точки и С (х; у) – середина отрезка АВ. Найдем координаты х, у точки С. Рассмотрим сначала случай, когда отрезок АВ не параллелен оси Оу, т.е. х1 ≠ х2. Проведем через точки А, В, С прямые, параллельные оси Оу (рис.4). Они пересекут ось Ох в точках А1 (х1; 0), В1 (х2; 0), С1 (х; 0). По теореме Фалеса (см. Приложение) точка С будет серединой отрезка А1В1. x= y=

Найдем координаты х, у точки С. Рассмотрим сначала случай, когда отрезок АВ не параллелен оси Оу, т.е. х ≠ х. Проведем через точки А, В, С прямые, параллельные оси Оу (рис.4). Они пересекут ось Ох в точках А1 (х1; 0), В1 (х2; 0), С1 (х; 0). По теореме Фалеса (см. Приложение 7) точка С1 будет серединой отрезка А1В1. Так как точка С1 – середина отрезка А1В1, то А1С1 = С1В1. при выбранном расположении точек имеем: А1С1 = х – х1, С1В1 = х – х1 И, значит, х – х1= х – х2, откуда 2) Аналогично получим: 3)

Основные формулы

Задача 4 Даны две вершины параллелограмма АВСD: А (0; 1) , С (3; 2). Найти координаты точки пересечения диагоналей. Решение. Точка пересечения диагоналей является серединой отрезка АС и имеет координаты:

Задача 5 Даны точки A(- 6; - 1), B(1;2) и C(- 3; - 2). Найдите координаты вершины M параллелограмма ABMC Решение.. Первый способ Координаты середины K(x0;y0) диагонали BC параллелограмма ABMC есть средние арифметические соответствующих координат концов отрезка BC, т.е. x0 = = - 1, y0 = = 0. Поскольку диагонали параллелограмма делятся точкой пересечения пополам, то K(x0;y0) — середина отрезка с концами в точках A(- 6; - 1) и M(x1;y1). Поэтому x0 = = - 1, y0 = = 0. Отсюда находим, что x1 = 4, y1 = 1. Второй способ.. Пусть x1, y1 — координаты точки M. Если ABMC — параллелограмм, то , а т.к. то x1 - 1 = 3, y1 - 2 = - 1. Отсюда находим, что x1 = 4, y1 = 1. Ответ: M(4;1).

5. Определение тригонометрических функций для любого угла от 0° до 180° До сих пор значение синуса, косинуса и тангенса были определены только для острых углов. Теперь мы определим их для любого угла от 0° до 180°. Возьмем окружность на плоскости хОу с центром в начале координат и радиусом R (рис.6). Пусть α – острый угол, который образует радиус ОА с положительной полуосью Ох. Пусть х и у – координаты точки А. Значение sin α и tg α для острого угла α выражаются через координаты точки А, а именно: sinα = , cosα = , tgα =

Определим теперь значения sin α, cos α и tg α для любого угла α. (Для tg α угол α = 90° исключается). Имеем: sin 90° = = 1, cos90° = = 0, sin180° = 0, cos180° =- = -1 Считая, что совпадающие лучи образуют угол 0°, будем иметь: sin0° = 0, cos0° = 1, tg0° = 0 Теорема: Для любого угла α, 0° < α < 180°, sin (180° - α) = sin α, cos (180° - α) = -cos α Для угла α ≠ 90° tg (180° - α) = -tg α

Задача 6 Вычислить: 1) sin 135°; 2) cos 135°; 3) 150° Решение. Согласно только что доказанной теореме sin 135° = sin (180°- 45°) = sin 45°; cos 135° = cos (180° - α) = -cos 45°; tg 150° = tg (180° - α) = -tg 30° Но sin 45° = √2/2, cos 45° = √2/2 , tg 30° = √3/3 Следовательно, sin 135° = √2/2, cos 135° = - √2/2, tg 135° = - √3/3

6. Применение координатной плоскости при решении алгебраических задач Задача 7 Изобразите на координатной плоскости множество точек, удовлетворяющих условию: х≥5 Решение: Решению неравенства удовлетворяет область, закрашенная розовым цветом

Задача 8 Покажите на координатной плоскости множество точек, которое задается неравенством Решение: Множество точек плоскости, удовлетворяющих данному неравенству, выделено на рисунке 8 серым цветом.

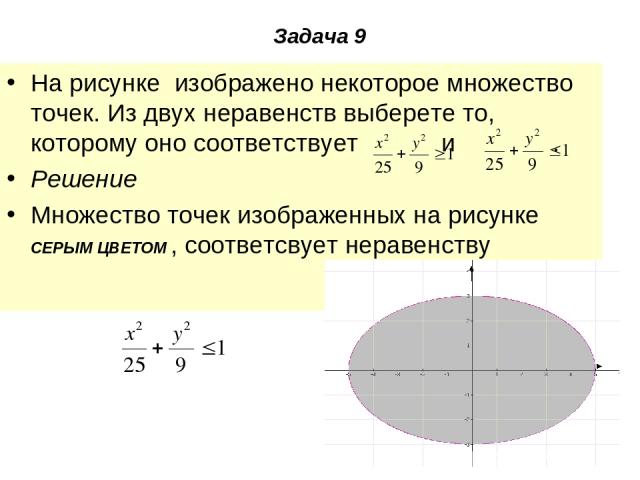
Задача 9 На рисунке изображено некоторое множество точек. Из двух неравенств выберете то, которому оно соответствует и . Решение Множество точек изображенных на рисунке СЕРЫМ ЦВЕТОМ , соответсвует неравенству

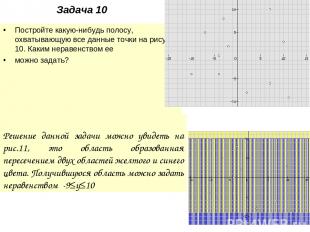
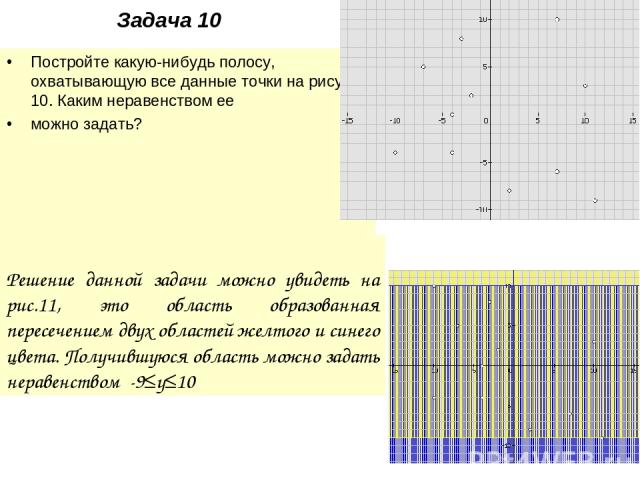
Задача 10 Постройте какую-нибудь полосу, охватывающую все данные точки на рисунке 10. Каким неравенством ее можно задать? Решение: Решение данной задачи можно увидеть на рис.11, это область образованная пересечением двух областей желтого и синего цвета. Получившуюся область можно задать неравенством -9≤у≤10

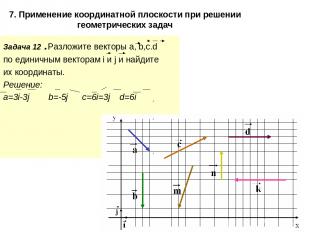
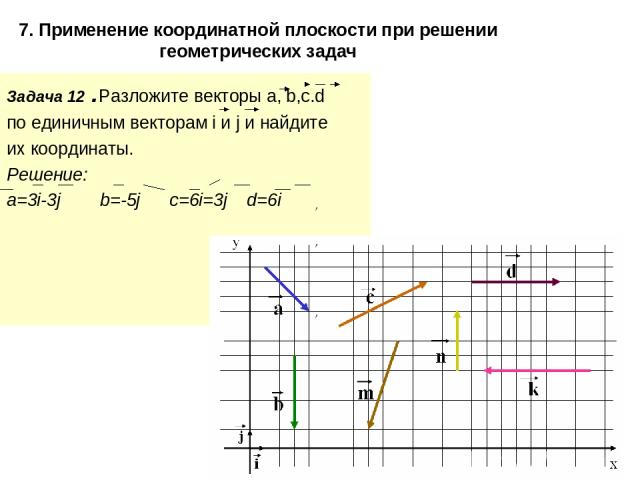
7. Применение координатной плоскости при решении геометрических задач Задача 12 .Разложите векторы а, b,c.d по единичным векторам i и j и найдите их координаты. Решение: a=3i-3j b=-5j c=6i=3j d=6i , , ,

Задача 11 Решить графически систему уравнений Решение:Графиком уравнения х2+у2=25 является окружность с центром в начале координат и радиусом, Равным5. Графиком уравнения ху=12 является Гипербола у=12:х. Построив графики в одной системе координат (рис.11), найдём координаты точек А, В, С, Д пересечения окружности и гиперболы: А(4; 3), В(3; 4), С(-4; -3), Д(-3; -4). Значит, решения заданной системы таковы: (4;3), (3;4), (-4;-3), (-3; -4).

Задача 13 На координатной плоскости заданы точки A(1;3), B(1;9), C(6;8) и E(5;1). Найдите площадь пятиугольника ABCDE, где D — точка пересечения прямых AC и BE. Решение Если y1y2 и x1x2, то уравнение прямой, проходящей через точки (x1;y1) и (x2;y2), имеет вид = Ответ:21

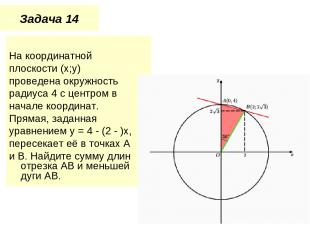
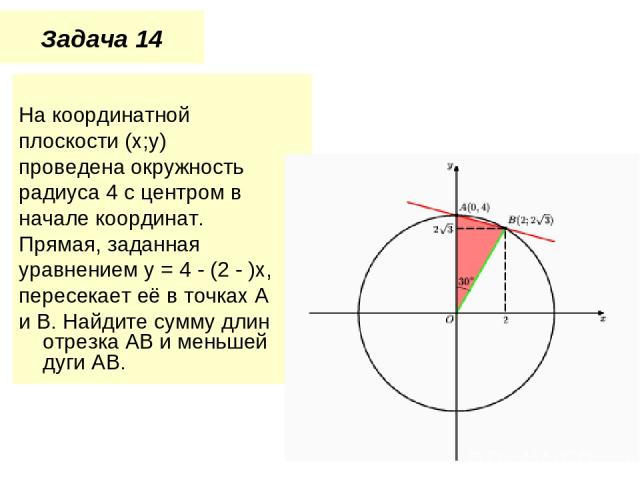
Задача 14 На координатной плоскости (x;y) проведена окружность радиуса 4 с центром в начале координат. Прямая, заданная уравнением y = 4 - (2 - )x, пересекает её в точках A и B. Найдите сумму длин отрезка AB и меньшей дуги AB.

Решение Решив систему уравнений Найдем координаты точек пересечения прямой и окружности: А(0;4), В(2,2;). Тогда, АВ = Пусть О- начало координат. По теореме косинусов из треугольника АОB находим, что cos∕AOB= . Поэтому градусная мера меньшей дуги АВ равна 300.Длина этой дуги равна одной двенадцатой длины окружности радиуса 4, т.е. . . Следовательно, искомая сумма равна +4 Ответ: +4 .

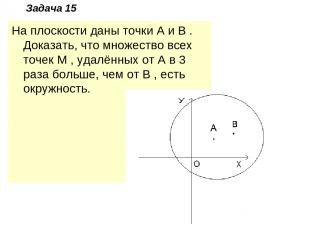
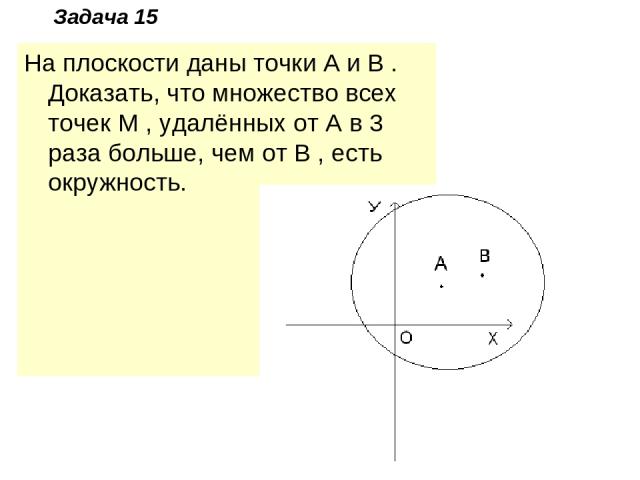
Задача 15 На плоскости даны точки A и B . Доказать, что множество всех точек M , удалённых от A в 3 раза больше, чем от B , есть окружность.

Решение Решим задачу координатным методом. Введём систему координат таким образом, чтобы A находилась в начале координат, а B имела координаты (1;0) . Пусть точка M(x,y) – искомая. Тогда 1/3=MB/MA= . Отсюда получаем x2+y2=9((x-1) 2+y2 , 8x2-18x+8(x- ) 2+y2( )2- . Получили уравнение окружности. Следовательно, все точки M данного множества лежат на окружности. Далее, так как все наши преобразования были равносильными, то любая точка, лежащая на окружности, заданной получившимся уравнением, будет принадлежать данному множеству. y2+9=0 , x2- x+y2+ =0; x2-2· x+( )2+y2+ -( )2=0;