Презентация на тему: График функции и его перемещение в координатной плоскости

График функции и его перемещение в координатной плоскости.

Определение модуля. Модулем числа называется расстояние от нуля до заданной точки на числовой прямой. | 6 | = 6 | 0 | = 0 | - 6 | = 6Так как расстояние отрицательным быть не может, то и значение модуля любого числа неотрицательно, таким образом получим ещё одно определение модуля:

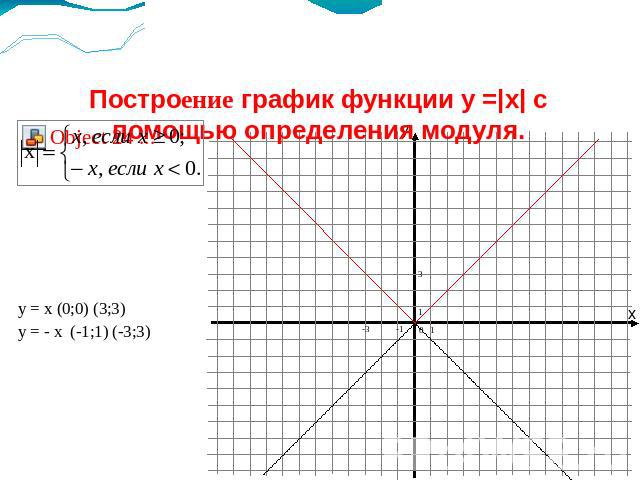
Построение график функции y =|x| с помощью определения модуля. y = x (0;0) (3;3) y = - x (-1;1) (-3;3)

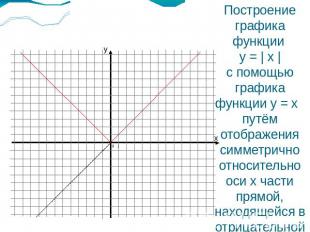
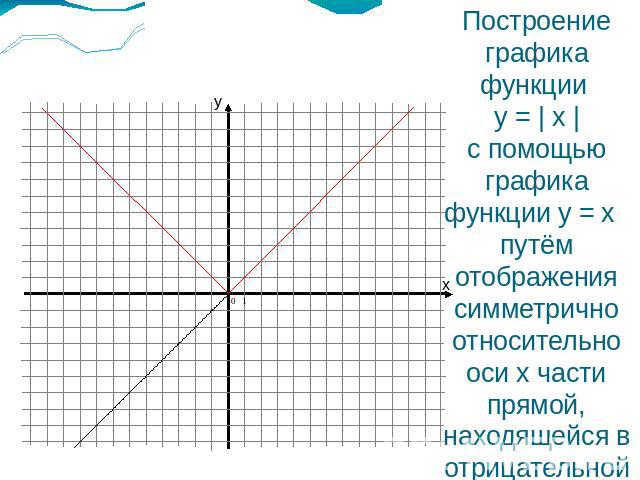
Построение графика функции y = | x |с помощью графика функции y = x путём отображения симметрично относительно оси х части прямой, находящейся в отрицательной области.

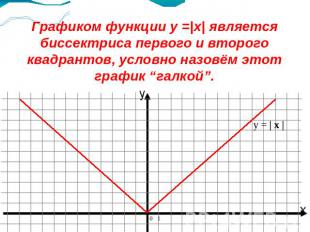
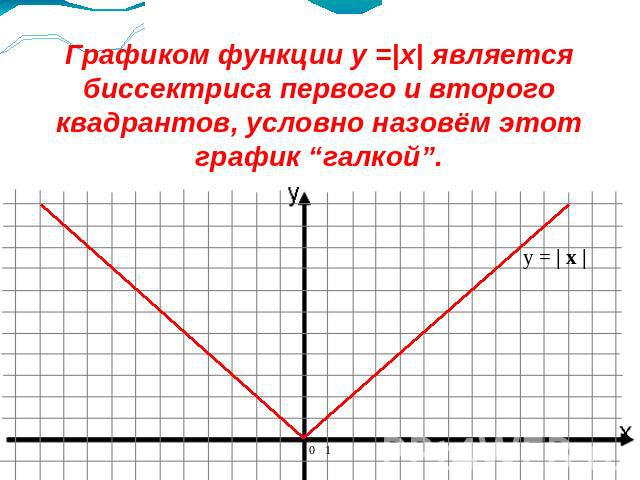
Графиком функции y =|x| является биссектриса первого и второго квадрантов, условно назовём этот график “галкой”.

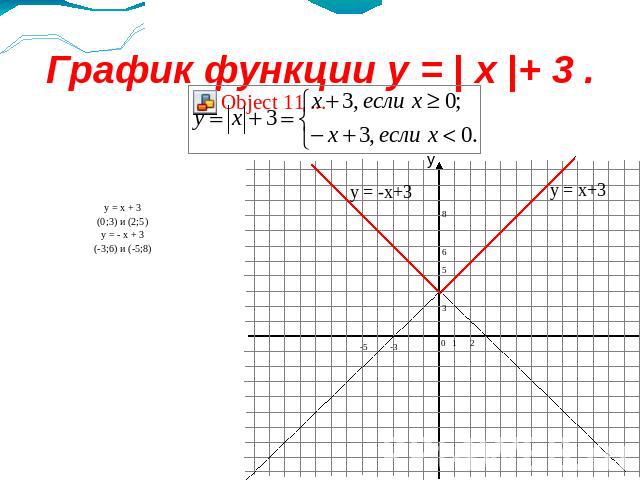
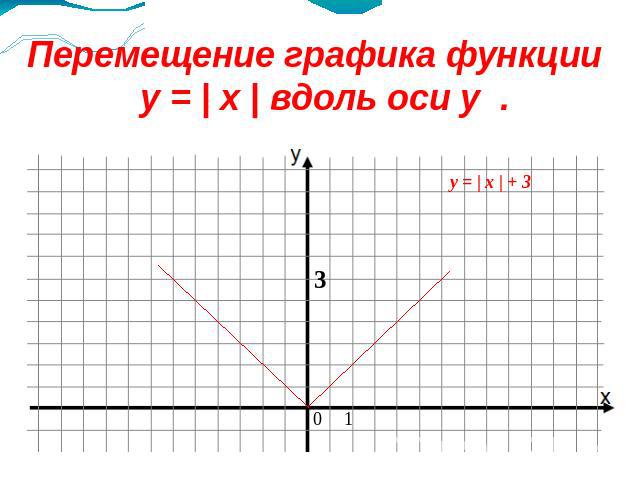
График функции y = | x |+ 3 . y = x + 3(0;3) и (2;5)y = - x + 3(-3;6) и (-5;8)

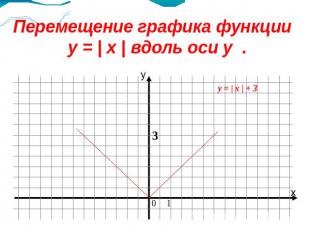
Перемещение графика функции y = | x | вдоль оси у .

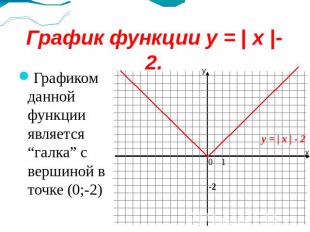
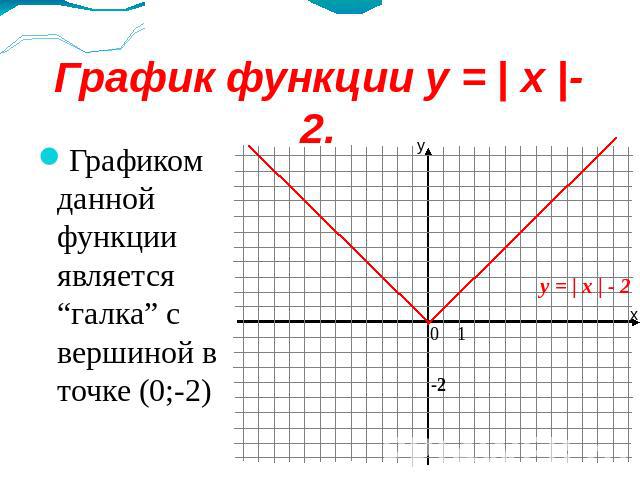
График функции y = | x |- 2. Графиком данной функции является “галка” с вершиной в точке (0;-2)

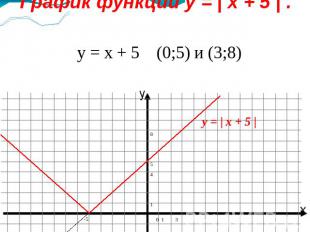
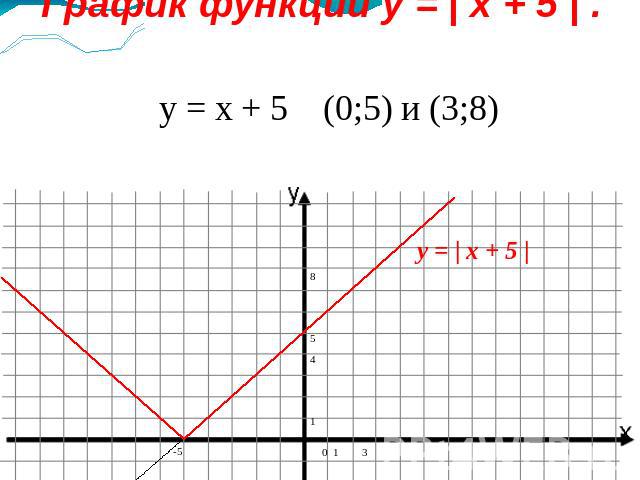
График функции y = | x + 5 | . y = x + 5 (0;5) и (3;8)

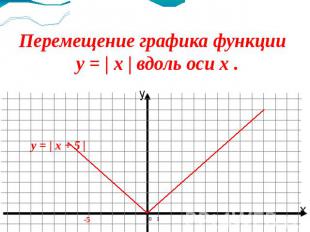
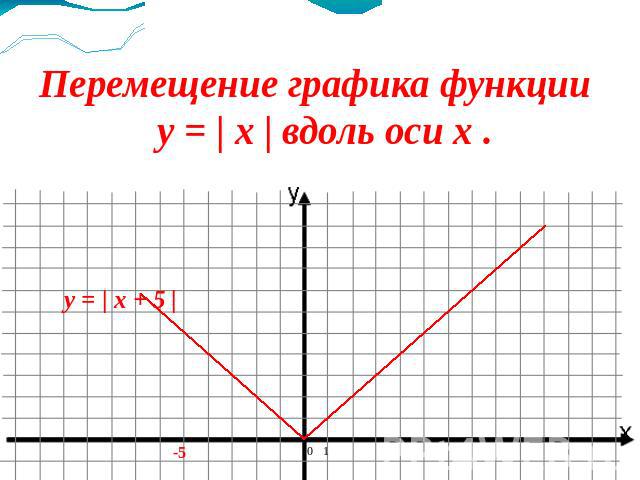
Перемещение графика функции y = | x | вдоль оси x .

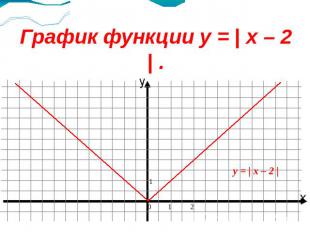
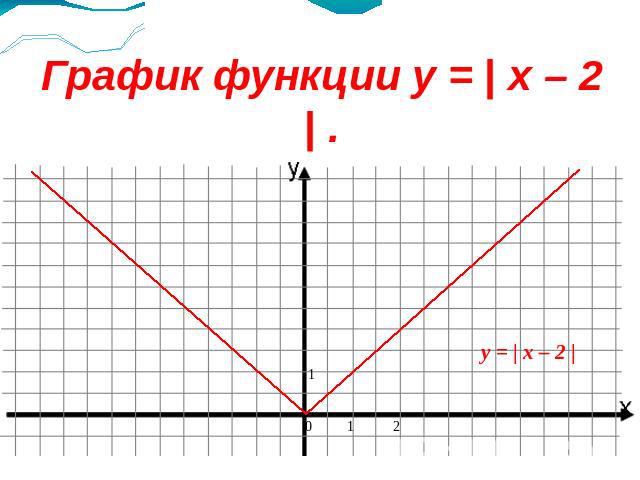
График функции y = | x – 2 | .

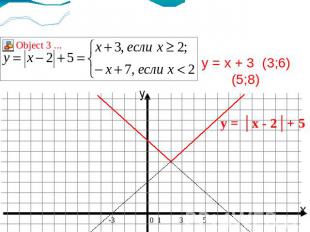
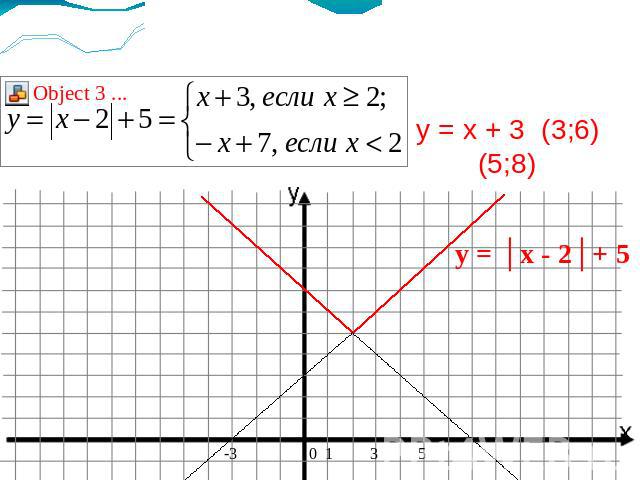
у = x + 3 (3;6) (5;8)у = - x + 7 (1;6) (-3;11) y = │x - 2│+ 5

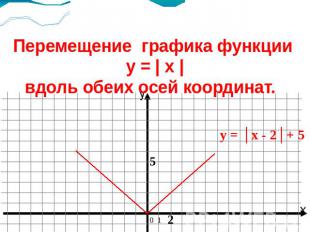
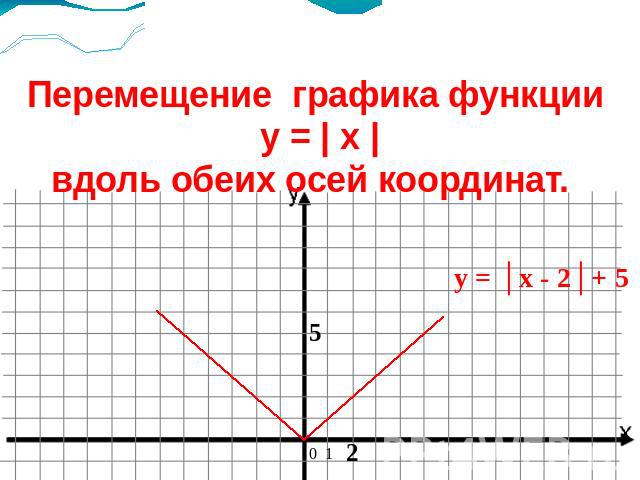
Перемещение графика функции y = | x |вдоль обеих осей координат.

Итак, в общем виде получили, что графиком функции: 1) y = |x| + m является “галка” с вершиной в (0;m)2) y = | x + n | является “галка” c вершиной в (-n;0)3) y = | x + n | + m является ”галка” с вершиной в (-n;m).

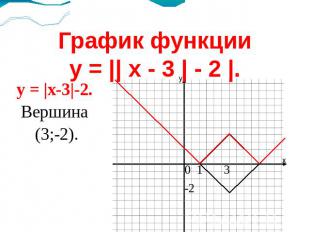
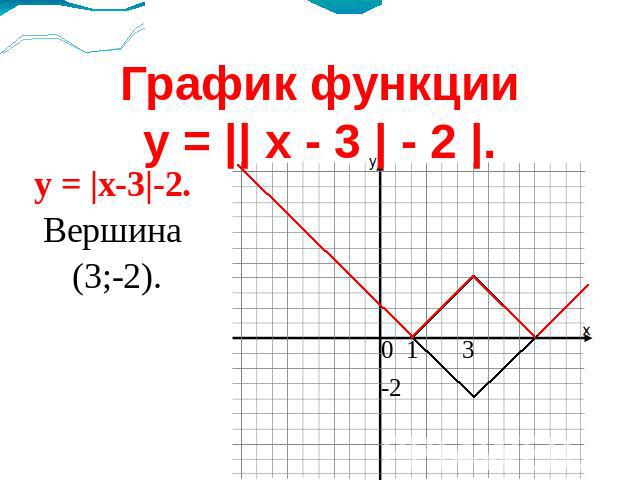
График функцииy = || x - 3 | - 2 |. y = |x-3|-2.Вершина (3;-2).

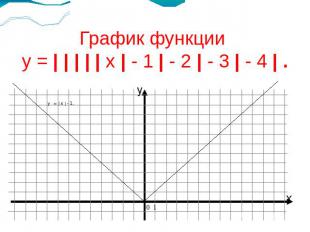
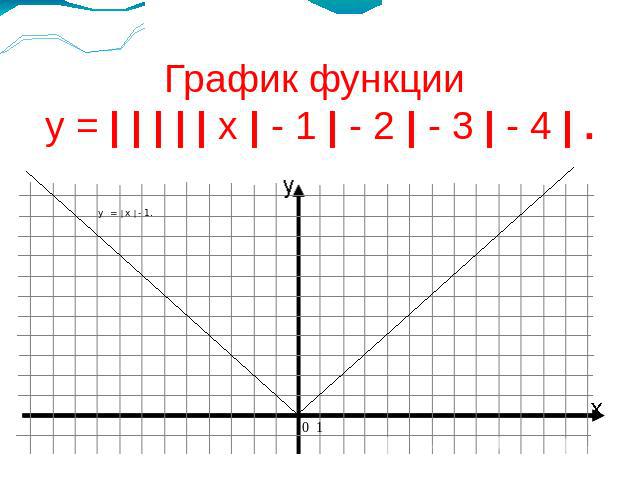
График функции у = | | | | | х | - 1 | - 2 | - 3 | - 4 | . у = | х | - 1.

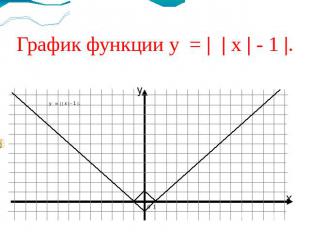
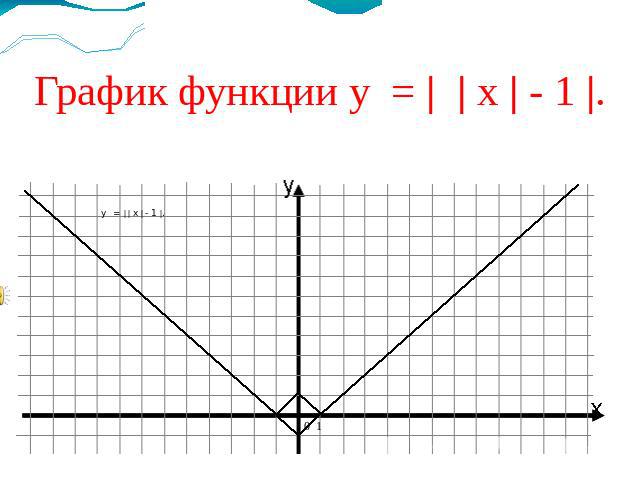
График функции у = | | х | - 1 |.у = | | х | - 1 |.

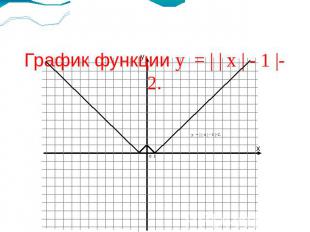
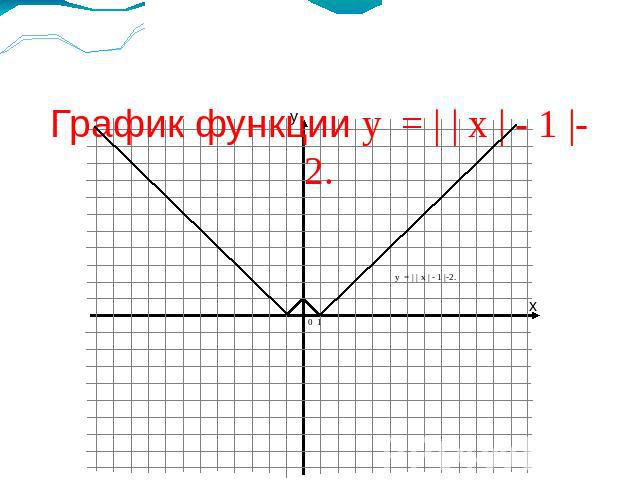
График функции у = | | х | - 1 |-2.у = | | х | - 1 |-2.

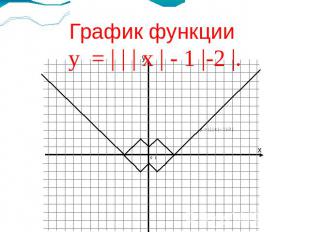
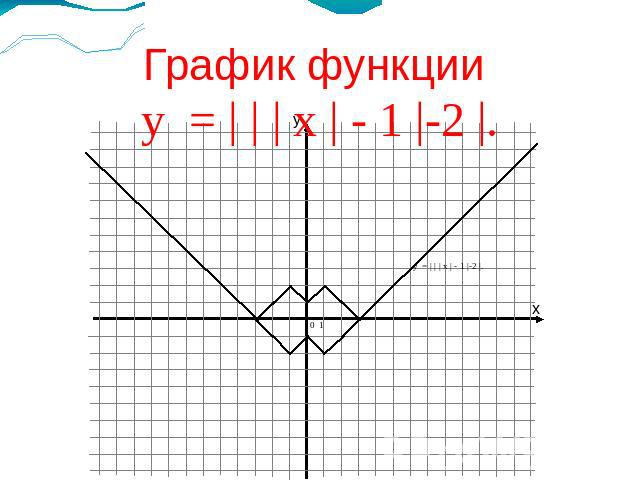
График функции у = | | | х | - 1 |-2 |.у = | | | х | - 1 |-2 |.

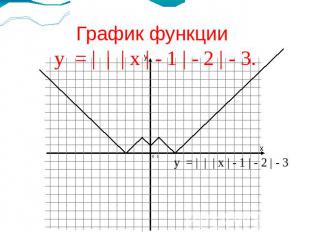
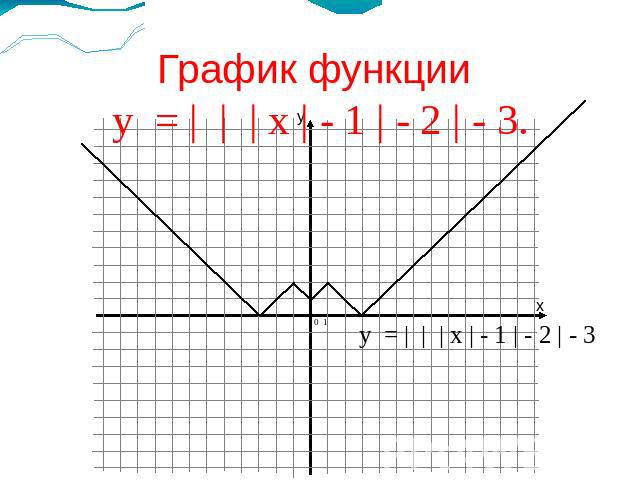
График функции у = | | | х | - 1 | - 2 | - 3.

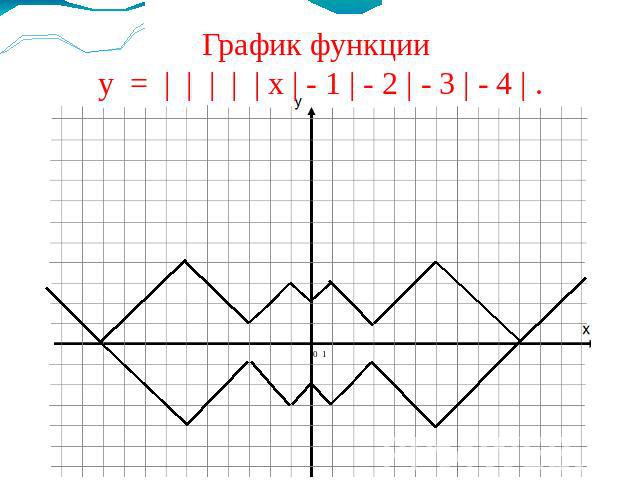
График функции у = | | | | х | - 1 | - 2 | - 3 | .

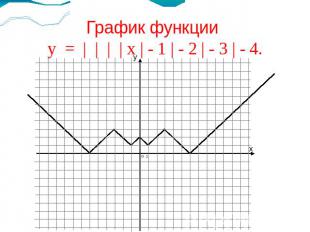
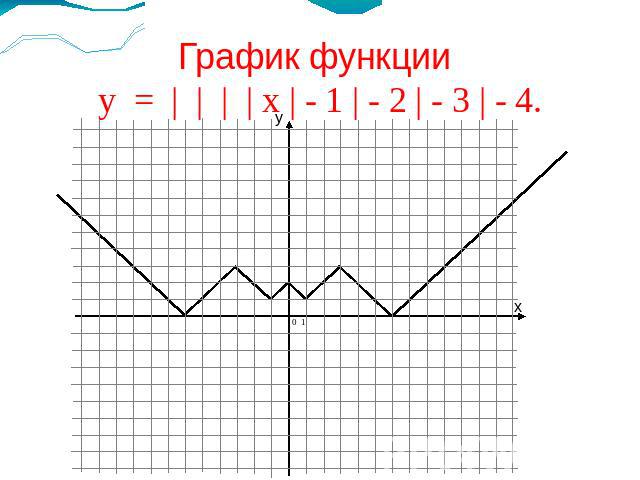
График функции у = | | | | х | - 1 | - 2 | - 3 | - 4.

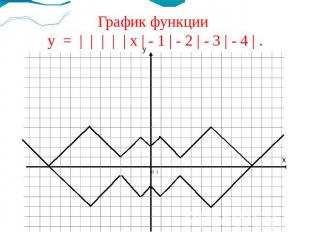
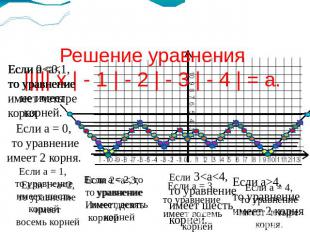
Решение уравнения ||||| х | - 1 | - 2 | - 3 | - 4 | = а. Если 0<a<1,то уравнение имеет четыре корня Если а = 0, то уравнение имеет 2 корня. Если а = 1, то уравнение имеет шесть корней Если 2<a<3,то уравнение Имеет десять корней Если а = 3, то уравнение имеет восемь корней Если а>4,то уравнение имеет 2 корня