Презентация на тему: Методы вычисления площадей фигур

Работа учителя математики МОУ «СОШ №42» г. Воркуты Курылевой Э. Р. 900igr.net

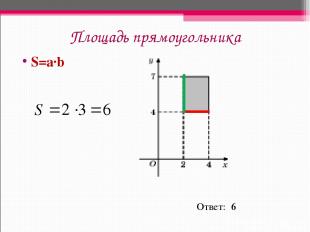
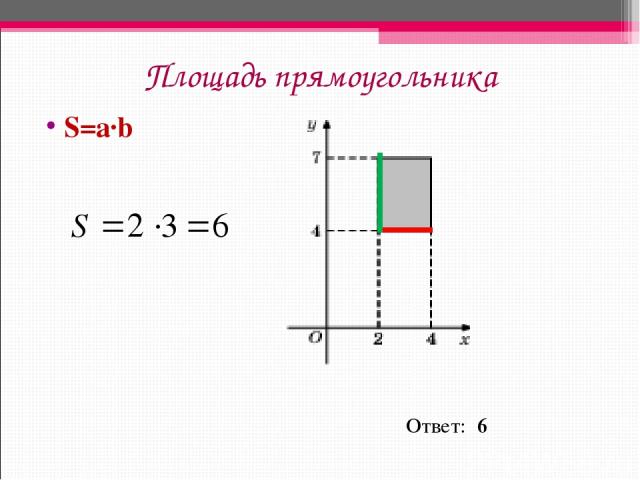
Площадь прямоугольника S=a∙b Ответ: 6

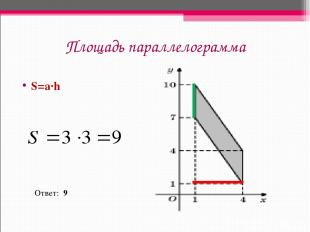
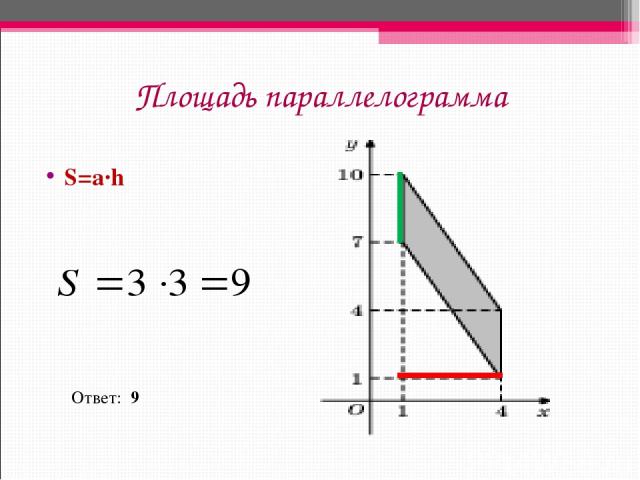
Площадь параллелограмма S=a∙h Ответ: 9

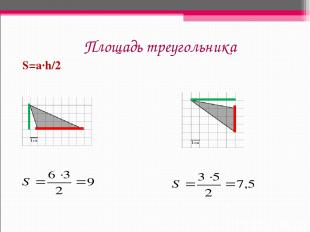
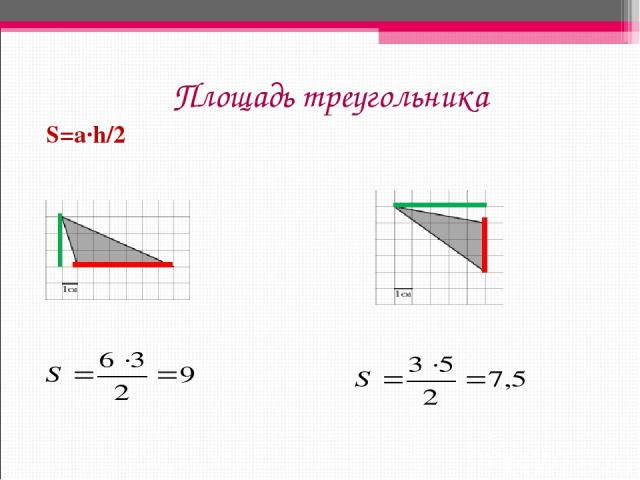
Площадь треугольника S=a∙h/2

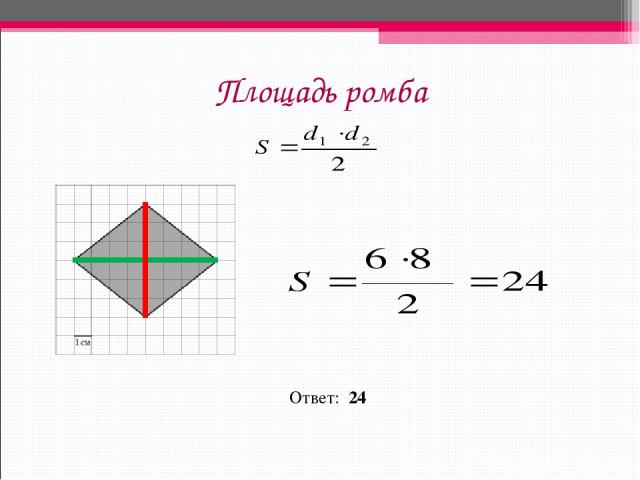
Площадь ромба Ответ: 24

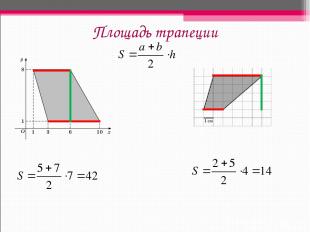
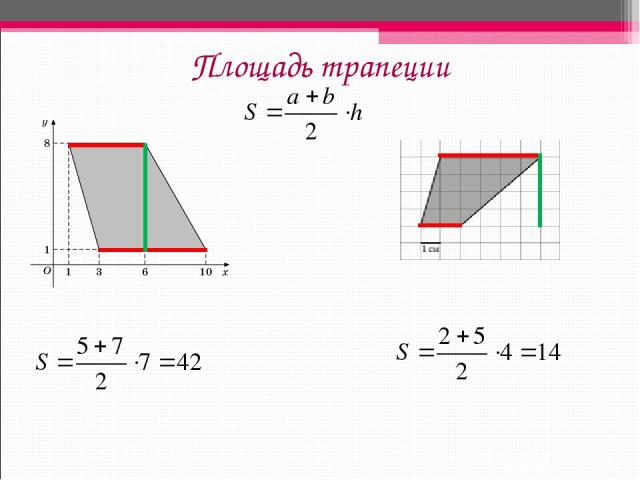
Площадь трапеции

Площадь кольца Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны        . Ответ: 104

????????????????????????????????

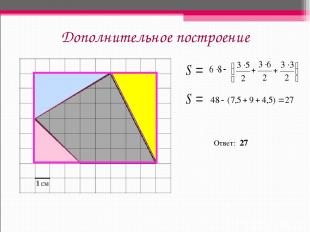
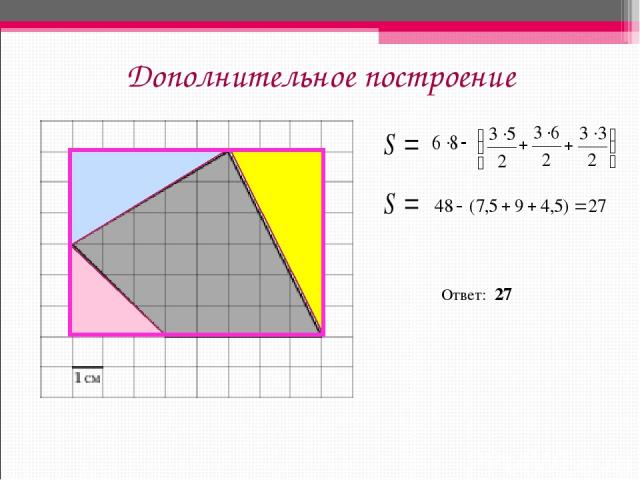
Дополнительное построение Ответ: 27

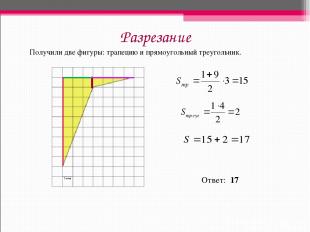
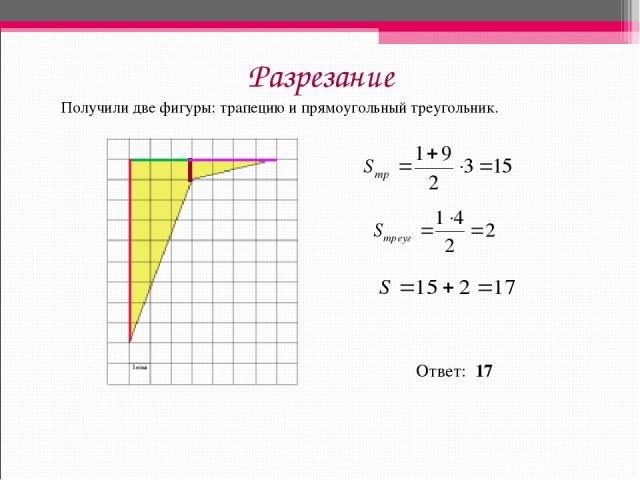
Разрезание Получили две фигуры: трапецию и прямоугольный треугольник. Ответ: 17

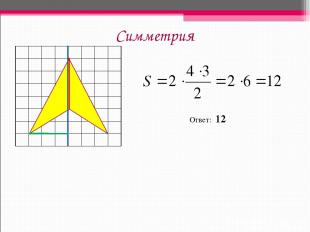
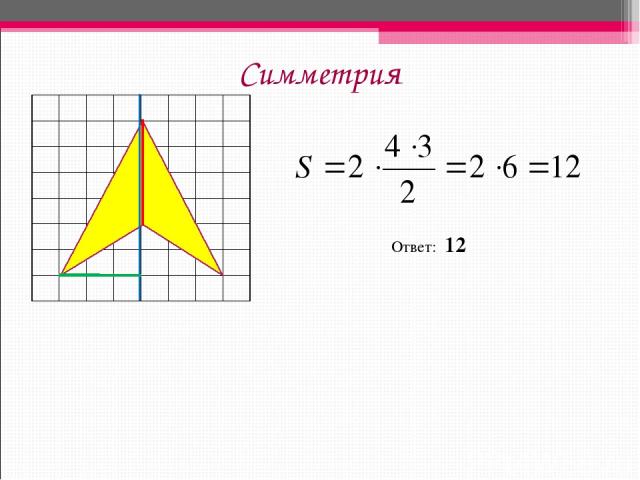
Симметрия Ответ: 12

Формула Пика Георг Алекса ндр Пик (10.08.1859-13.07.1942) , австрийский математик. 

Теорема Пика для вычисление площади многоугольника с целочисленными вершинами .  Пусть  L — число целочисленных точек внутри многоугольника,    B— количество целочисленных точек на его границе,   S— его площадь. Тогда справедлива формула Пика: S=L+B/2-1

Мы будем пользоваться этой в более удобном для нас виде. Введём другие обозначения: В - число целочисленных точек внутри многоугольника,    Г - количество целочисленных точек на его границе, тогда формула Пика будет иметь вид: S=В+Г/2-1

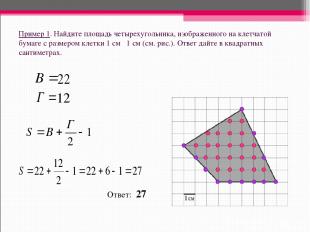
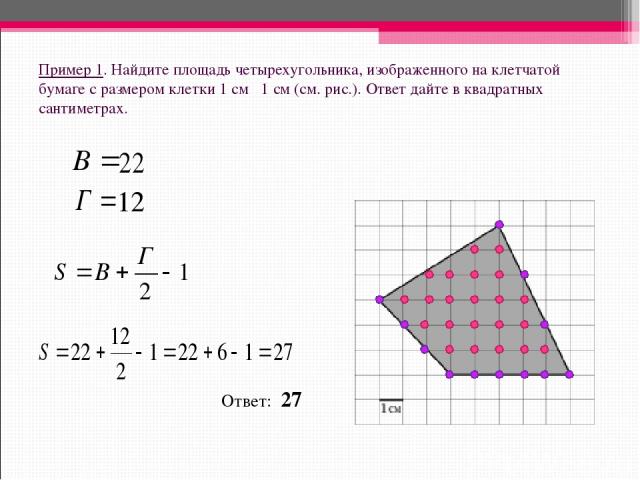
Пример 1. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см   1 см (см. рис.). Ответ дайте в квадратных сантиметрах. Ответ: 27

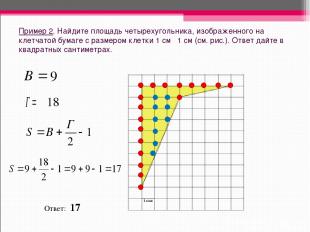
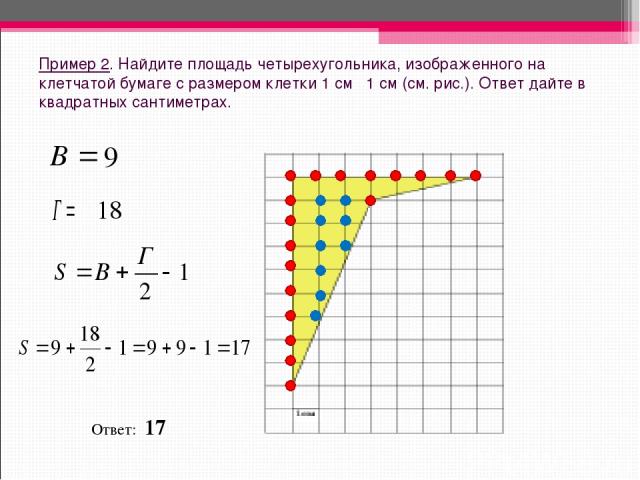
Пример 2. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см   1 см (см. рис.). Ответ дайте в квадратных сантиметрах. Ответ: 17

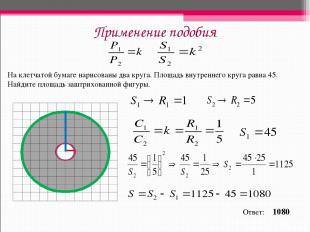
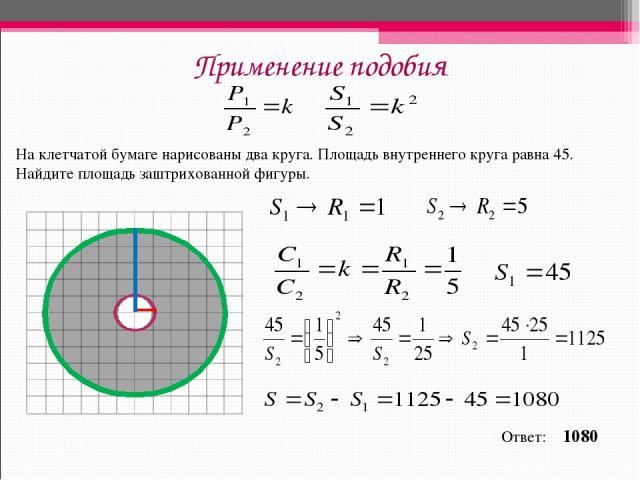
Применение подобия На клетчатой бумаге нарисованы два круга. Площадь внутреннего круга равна 45. Найдите площадь заштрихованной фигуры. Ответ: 1080

Итоги занятия При решении задач на нахождение площадей фигур можно использовать следующие методы: 1. Основные формулы вычисления площадей плоских фигур. 2. Метод дополнительного построения . 3. Метод разрезания. 4. Формула Пика. 5. Применение подобия. 6. Осевая симметрия.

Удачи в учёбе и на ЕГЭ!